旅行推销员问题:基于问题
此示例显示如何使用二进制整数程序来解决经典旅行推销员问题。这个问题涉及通过一组停止(城市)找到最短的闭幕之旅(路径)。在这种情况下,有200个停止,但你可以轻松改变nStops变量以获得不同的问题大小。您将解决初始问题,并看到解决方案具有子故事。这意味着找到的最佳解决方案不会通过所有点给出一个连续路径,而是有几个断开连接的环。然后,您将使用迭代过程来确定子资源,添加约束,并重新运行优化,直到消除子流程。
关于这个问题的基于求解器的方法,请参见旅行推销员问题:基于求解器.
问题公式化
用公式表示整数线性规划的旅行商问题:
生成所有可能的旅行,这意味着所有不同的站点都有。
计算每次旅行的距离。
要最小化的代价函数是旅途中每次行程的行程距离之和。
决策变量是二元的,并且与每个行程相关联,其中每个1表示在行程中存在的行程,每个0表示不在行程中。
为确保行程包含每一站,应包含每一站正好包含两趟行程的线性约束。这意味着一次到达,一次离开。
生成停止
在美国大陆大陆的原油多边形表示内产生随机停止。
负载(“usborder.mat”,'X','是','xx','yy');rng (3“旋风”)在缅因州和佛罗里达州停留,并可复制nstops = 200;%您可以使用任何数字,但问题大小尺度为n ^ 2stopslon = zeros(nstops,1);%分配nStops的x坐标stopsLat = stopsLon;%分配坐标n = 1;尽管(n <= nStops) xp = rand*1.5;yp =兰德;如果inpolygon (xp, yp, x, y)如果在边界内,则% tTeststopslon(n)= xp;stopslat(n)= yp;n = n + 1;结束结束
计算点之间的距离
因为有200个停止,有19,900个旅行,意思是19,900个二进制变量(#变量= 200选择2)。
生成所有的旅行,这意味着所有的站点。
idx = nchoosek (1: nStops, 2);
计算所有行程距离,假设地球是平坦的,以便使用毕达哥拉斯族规则。
dist = armot(stopslat(Idxs(:,1)) - stopslat(Idxs(:,2)),...stopslon(IDXS(:,1)) - stopslon(IDXS(:,2)));lendist =长度(dist);
根据这个定义dist向量,旅行的长度是
dist”*旅行
在哪里旅行是表示解的行程的二进制向量。这是你试图最小化的旅行距离。
创建图形和绘制地图
将问题表示为图形。创建一个图表,停止是节点,并且跳闸是边缘。
g =图表(IDXS(:,1),IDXS(:,2));
使用图形图显示停止。绘制没有图边的节点。
图= plot(g,“XData”,stopslon,'ydata'stopsLat,'linestyle',“没有”,'nodelabel',{});持有在绘制外部边界绘图(x,y,的r -) 抓住离开
创建变量和问题
使用表示潜在旅行的二进制优化变量创建优化问题。
tsp = optimproblem;旅行= optimvar (“旅行”lendist 1'类型','整数',下界的,0,“UpperBound”,1);
包括问题的目标函数。
tsp.objective = dist'* traps;
约束
创建线性约束,使每个站点有两个相关的行程,因为必须有到每个站点的行程和离开每个站点的行程。
使用图形表示来识别通过查找连接到该停止的所有边缘在停止时启动或结尾的所有旅行。对于每个停止,创建该约束,即该停止等级等于两个的程和。
CONSTR2TRIPS = OPEMCONSTR(NSTOPS,1);为stop = 1:nstops idxs =超越(g,stop);识别与停车相关的行程constr2trips(stop) = sum(trips(which hidxs)) == 2;结束tsp.Constraints。constr2trips = constr2trips;
解决最初的问题
这个问题随时可以解决。若要抑制迭代输出,请关闭默认显示。
选择= optimoptions ('intlinprog','展示','离开');tspsol =解决(茶匙,'选项'选择)
Tspsol =结构与字段:旅行(19900×1双):
可视化解决方案
使用解决方案TRIPS创建一个新图形作为边缘。为此,请在某些值不完全整数的情况下绕过解决方案,并将结果值转换为逻辑.
tspsol。旅行= logical(round(tspsol.trips)); Gsol = graph(idxs(tspsol.trips,1),idxs(tspsol.trips,2),[],numnodes(G));%GSOL =图表(IDXS(TSPSOL.TRIPS,1),IDXS(TSPSOL.TRIPS,2));在大多数情况下,%也有效
将新图形覆盖在现有的图形上,并突出其边缘。
持有在突出显示(高音,GSOL,'linestyle',“- - -”) 标题(“解决方案与Subtours”)
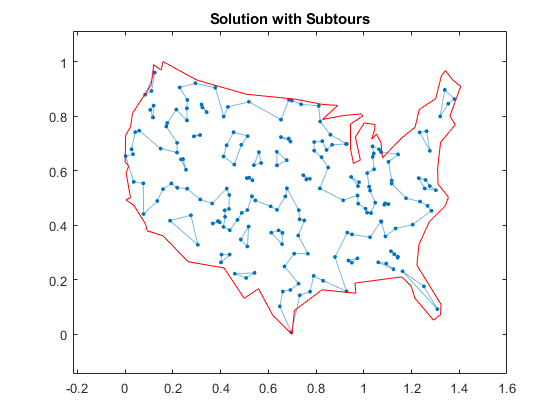
可以在地图上看到,解决方案有几个子流。指定到目前为止指定的约束不会阻止这些子房子发生。为了防止任何可能的子学会发生,您需要一个令人难以置信的大量不等式约束。
Subtour约束
因为您无法添加所有子资金的约束,所以采取迭代方法。检测当前解决方案中的子流,然后添加不等式约束,以防止这些特定的子流程发生。通过这样做,您可以在几个迭代中找到适当的巡演。
消除带有不等式约束的子行程。举个例子,如果你在一个子游览中有五个点,那么你有五条线连接这些点来创建子游览。通过实现一个不等式约束来消除这个子过程,即这5个点之间必须小于或等于4条线。
甚至更多,在这五点之间找到所有线条,并限制解决方案不超过四条线的存在。这是一个正确的约束,因为如果在解决方案中存在五个或更多行,则解决方案将有一个子流(图表 节点和 边总是包含一个循环)。
通过识别中连接的组件来检测子行程GSOL.,使用当前解决方案中的边缘构建的图形。Conncomp.返回带有每个边缘所属的子流量的向量的向量.
tourIdxs = conncomp (Gsol);numtours = max (tourIdxs);%分游次数流('子房子数量:%d \ n',numtours);
子房子数量:27
包括线性不等式约束来消除子环,并反复调用求解器,直到只剩下一个子环。
子台楼的添加约束的%索引k = 1;尽管numtours > 1重复,直到只有一个子游览%添加子游览约束为ii = 1:numtours inSubTour = (tourIdxs == ii);当前子游览中的边a =所有(Insubtour(Idxs),2);%在子环中两端的完全图索引constrname =“subtourconstr”+ num2str(k);TSP.Constraints。(CONSTRNAME)= SUM(TRIPS(A))<=(NNZ(INERUBTOUR) - 1);k = k + 1;结束%尝试再次优化[tspsol, fval exitflag、输出]=解决(茶匙,'选项'、选择);tspsol。旅行= logical(round(tspsol.trips)); Gsol = graph(idxs(tspsol.trips,1),idxs(tspsol.trips,2),[],numnodes(G));%GSOL =图表(IDXS(TSPSOL.TRIPS,1),IDXS(TSPSOL.TRIPS,2));在大多数情况下,%也有效绘制新溶液hGraph。线型=“没有”;%删除前面突出显示的路径突出显示(高音,GSOL,'linestyle',“- - -”)绘制这次有多少次短途旅行?tourIdxs = conncomp (Gsol);numtours = max (tourIdxs);%分游次数流('子房子数量:%d \ n'numtours)结束
子房子数量:20
子房子数量:7
子房子数量:9
子房子数量:9
副数量:3
副数量:2
子房子数量:7
副数量:2
子房子数量:1
标题(“取消子行程的解决方案”);持有离开

解决方案质量
这个解代表了一个可行的旅行,因为它是一个单闭环。但是这是一种低成本的旅行吗?找出答案的一种方法是检查输出结构。
disp (output.absolutegap)
0
绝对间隙的小意味着解是最优的或有一个接近最优的总长度。

