用高精度算术找到几乎整数

打开实时脚本

寻找整数关系[1]的算法，如PSLQ算法，需要高精度的算术来产生准确的结果。算法输入的精度越高，算法就越有信心找到一个整数关系，而不仅仅是一个数值人工制品。PSLQ算法可能会遇到假阳性，例如由几乎整数引起的假阳性。

这个例子展示了如何使用Symbolic Math Toolbox™中的变精度算术来查找几乎整数，或者非常接近整数的数字。此示例搜索具有此形式的几乎整数(或近整数) $经验值（ π \sqrt{n} ）$ 或 $经验值（ π n ）$ 对于整数 $n ＝ 1 ，．．．， 200$ ．

首先，考虑一个众所周知的例子，一个几乎是整数的实数[2] $经验值（ π \sqrt{163} ）$ ．将这个实数创建为一个精确的符号数。

R = exp(pi*√(sym(163)))

r =
                  $e^{π \sqrt{163}}$

用可变精度算术计算此数字vpa．默认情况下,vpa计算值为32位有效数字。

vpa(右)

ans =
                  $262537412640768743.99999999999925$

可以使用。将有效位数更改为更高的精度数字．计算相同的数字为40位有效数字。

数字(40)vpa(右)

ans =
                  $262537412640768743.9999999999992500725972$

这个数字非常接近整数。求这个实数与它最接近的整数之差。使用vpa将此结果计算为40位有效数字。

Dr = vpa(圆(r)-r)

博士=
                  $0.0000000000007499274028018143151532171817442410122968$

接下来，搜索具有该形式的几乎整数 $经验值（ π \sqrt{n} ）$ 对于整数 $n ＝ 1 ，．．．， 200$ ．将这些数字创建为精确的符号数字。

A = exp(pi*√(sym(1:200)));

有效位数设置为的整数部分的位数 $经验值（ π \sqrt{200} ）$ 加上小数点后20位。

d = log10(A(end));数字(上格(d) + 20)

计算这一系列数字与它们最接近的整数之间的差值。找到舍入误差小于0.0001的几乎整数。以精确的符号形式显示结果。

B = vpa(round(A)-A);A(abs(B)<0.0001)'

A_nearint =
                 
                   $（ \begin{array}{c} e^{π \sqrt{37}} \\ e^{π \sqrt{58}} \\ e^{π \sqrt{67}} \\ e^{π \sqrt{163}} \end{array} ）$

以至少20个小数点的精度计算几乎整数。

A_nearint = vpa(A_nearint)

A_nearint =
                 
                   $（ \begin{array}{c} 199148647.9999780465518567665009238753359 \\ 24591257751.99999982221324146957619235527 \\ 147197952743.9999986624542245068292613126 \\ 262537412640768743.9999999999992500725972 \end{array} ）$

绘制差异的直方图以显示其分布。分布中出现了许多接近于零的差异，其中形式为 $经验值（ π \sqrt{n} ）$ 几乎是整数。

柱状图(双(B), 40)

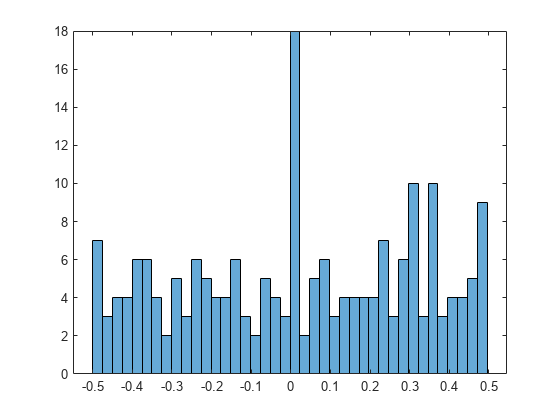
图中包含一个轴对象。坐标轴对象包含一个直方图类型的对象。

接下来，搜索具有该形式的几乎整数 $经验值（ π n ）$ 对于整数 $n ＝ 1 ，．．．， 200$ ．将这些数字创建为精确的符号数字。

A = exp(sym(pi)*1:200);

有效位数设置为的整数部分的位数 $经验值（ π \cdot 200 ）$ 加上小数点后20位。

d = log10(A(end));数字(上格(d) + 20)

计算这一系列数字与它们最接近的整数之间的差值。找到舍入误差小于0.0001的几乎整数。结果为空信谊数组，这意味着几乎没有整数满足这个条件。

B = vpa(round(A)-A);A_nearint = A(abs(B)<0.0001)

A_nearint =空sym: 1乘0

绘制差异的直方图。直方图分布比较均匀，显示了窗体 $经验值（ π n ）$ 几乎整数出现的次数不多。对于这个特定的示例，没有舍入误差小于0.0001的几乎整数。

柱状图(双(B), 40)

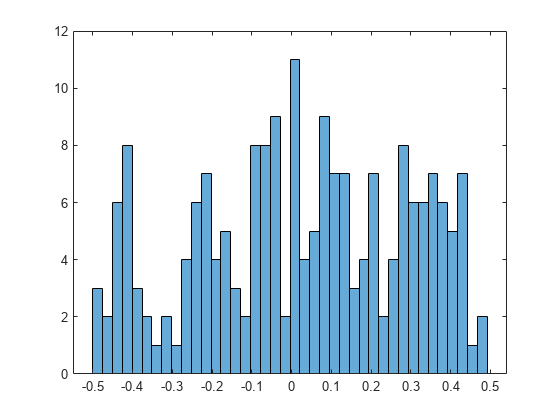
图中包含一个轴对象。坐标轴对象包含一个直方图类型的对象。

最后，恢复32位有效数字的默认精度，以便进行进一步的计算。

数字(32)

参考文献

[1]“整数关系算法。”维基百科，2022年4月9日。https://en.wikipedia.org/w/index.php?title=Integer_relation_algorithm&oldid=1081697113．

[2]“几乎整数。”维基百科，2021年12月4日。https://en.wikipedia.org/w/index.php?title=Almost_integer&oldid=1058543590．

另请参阅

信谊|vpa|数字

用高精度算术找到几乎整数

参考文献

另请参阅

相关的话题