用配点法求解带有边界层的非线性常微分方程
此示例示出了如何使用样条命令,从曲线拟合工具箱™解决非线性常微分方程(ODE)。
这个问题
我们考虑非线性奇异摄动问题
D^2g(x) + (g(x))^2 = 1 on [0..1]
Dg(0) = g(1) = 0。
这个问题已经是相当困难小量= 0.001,所以我们选择适度
小量= 0.1;
近似空间
我们从C^1具有指定的断裂序列的分段立体图中,通过配点法求出近似解休息,于是要了订单ķ是4。
符=(0:4)/ 4;K = 4;
我们获得相应的结序列
节= augknt(场所中,k,2)
节=1×140.2500 0.2500 0.5000 0.5000 0.7500 0.7500 1.0000 1.0000 1.0000 1.0000
无论的顺序和节的选择,相应的花键空间具有维
n =长度(节数)- k
N = 10
离散化
自由度的数目,10,很好地符合了我们期望在每个多项式块的两个位置上配置的事实,总共有8个条件,当我们把两个边的条件相加,就得到了10个条件。
我们选择两种高斯网站每个区间。对于单位长度的`标准”区间[-1/2 .. 1/2,这是两个位点
高斯= .5773502692 * [1/2;1/2);
从这一点,我们通过获取搭配网站的整个集合
ninterv =长度(减免)1;temp =(优惠(2:ninterv + 1) +优惠(1:ninterv)) / 2;temp = temp([1 1],:) + gauss*diff(break);colsites =临时(:)。';
数值问题
我们要解决的数值问题是找到一个分段多项式PP)ÿ对于给定的阶数和给定的节数,它满足非线性系统
Dy (0) = 0
(Y(X))^ 2 +小量d ^ 2Y(X)= 1在colsites X
y (1) = 0
线性化
如果ÿ是我们目前的近似解,然后向好(?)解决方案的线性问题ž按牛顿的方法读
DZ(0)= 0
w_0(x)的Z(x)的+小量d ^ 2Z(x)= B(X),用于colsites X
Z(1)= 0
同w_0(X):= 2Y(x)的和B(X):=(Y(X))^ 2 + 1。
事实上,通过选择w_0 (1): = 1,W_1(0):= 1,
w_2(x):= epsilon, w_1(x):= 0
然后选择其他的值w_0,W_1,W_2,b还没有被指定为零,我们可以给系统一个统一的形状
w_0 (x) z (x) + w_1 (x) Dz (x) + w_2 (x) ^ 2 z D b (x) = x (x)的网站
哪里
colsites网站= [0,1];
线性系统要解决的问题
该系统将其解的b样条系数转化为一个ž。对于这一点,我们需要的零,第一,并在每个二阶导数X在网站和每一个相关的B样条。这些值由所供给的spcol命令。
下面是对文件的重要组成部分spcol:
SPCOL b -样条配置矩阵。
COLLOC = SPCOL(knot,K,TAU)是矩阵
[D ^ m (i) B_j(τ(i)): i = 1:长度(τ),j = 1:长度(节)- k),
与d ^ M(ⅰ)B_j第m(I)B_j的倍衍生物,
K阶结点的第j个b样条,
一系列的地点,
这两个结和TAU被假定为单调不减,并
米(i)是整数#{Ĵ
TAU(i)在TAU中的“累积”多重性。
我们用spcol供应矩阵
colmat = spcol(节,K,brk2knt(位点,3));
同brk2knt用于将每一项乘以三网站,因此,我们得到colmat,对于每一个X在网站的值以及一阶和二阶导数X所有相关的B样条。
由此,我们结合与三联相关的行获得的搭配矩阵X使用重量w_0 (x) w_1 (x) w_2 (x)获得对应于行X我们的线性系统的矩阵。
需要Y的初始猜测
我们还需要一个当前近似值ÿ从样条空间。首先,我们通过插值一些合理的初始猜想从我们的pp空间网站。对于这个猜测,我们使用抛物线
x ^ 2 - 1
它满足终止条件并且在样条空间中。我们通过插值得到它的b型网站。我们从完整的矩阵中选择相关的插值矩阵colmat。以下是几个谨慎的步骤:
intmat = colmat([2 1+(1:(n-2))*3,1+(n-1)*3],:);coefs = intmat \ [0 colsites * colsites-1 0]'。Y = SPMAK(节,coefs');
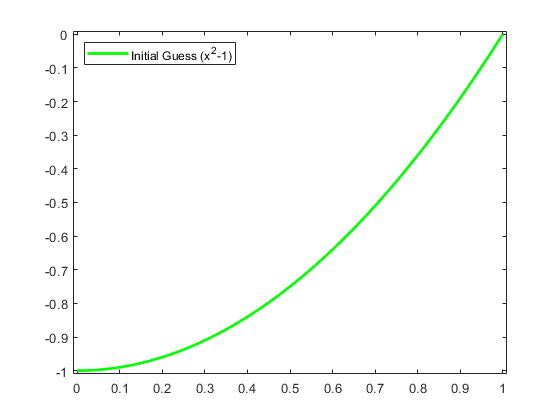
我们把结果画出来,应该是完全正确的X ^ 2-1。
fnplt (y,‘g’);传奇(“初始猜测(x ^ 2 - 1)”,“位置”,“西北”);轴([ - 0.01 1.01 -1.01 0.01]);保持在
迭代
我们现在可以完成线性系统的构造和求解,得到改进的近似解ž从我们目前的猜测ÿ。事实上,最初的猜测ÿ可用,我们现在成立了一个迭代的,将被终止时的变化z-y小于规定的公差。
公差= 6. e-9;
变化的最大范数z-y在每次迭代被示出为下面的输出,和如图所示的每个迭代的。
而1 VTAU = fnval(Y,colsites);权重= [0 1 0;[2 * VTAU“。零(N-2,1)repmat(ε,正2,1)];1 0 0];colloc =零(N,N);对于J = 1:N colloc(J,:) =权重(J,:)* colmat(3 *(J-1)+(1:3),:);结束coefs = colloc \ [0 VTAU * VTAU + 1 0。]'。Z = SPMAK(节,coefs');fnplt(Z,“k”);maxdif = MAX(最大值(ABS(z.coefs-y.coefs)));fprintf中(“maxdif = % g \ n”,maxdif)如果(maxdif <容差),打破,结束%现在重申y = z;结束
maxdif = 0.206695
maxdif = 0.01207
maxdif = 3.95151e-05
maxdif = 4.43216e-10
传奇({“初始猜测(x ^ 2 - 1)”“迭代”},“位置”,“西北”);

看起来像二次收敛,从牛顿迭代预期。
准备一个更小的
如果我们现在减少ε我们创造更多的右端点附近的边界层,这要求一个非均匀网。我们用newknt构建一个适当的(更细)从当前近似啮合。
纽结= newknt(z, ninterv+1);休息= knt2brk(节);节= augknt(休息,4,2);n =长度(节)- k;
搭配网站的新符
接下来,我们得到与新元素相对应的搭配点休息
ninterv =长度(减免)1;temp =((优惠(2:ninterv + 1) +优惠(1:ninterv)) / 2);temp = temp([1 1],:) + gauss*diff(break);colsites =临时(:)。';colsites网站= [0,1];
然后是新的配置矩阵。
colmat = spcol(节,K,brk2knt(位点,3));
最初的猜测
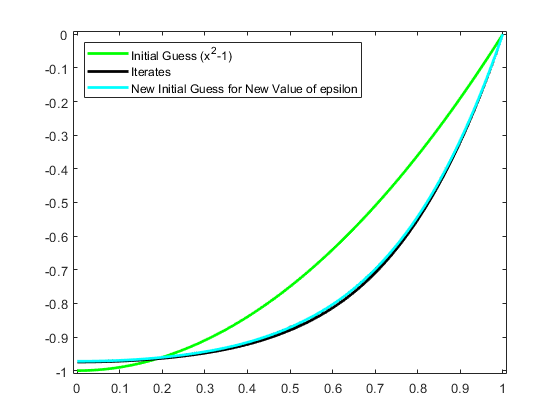
我们得到了最初的猜测ÿ作为从当前样条空间到计算解的插值ž。我们绘制产生插值可以肯定的 - 它应该是接近我们目前的解决方案。
intmat = colmat([2 1+(1:(n-2))*3,1+(n-1)*3],:);y = spmak(结,[0 fnval(z,colsites) 0]/intmat.');fnplt (y,'C');甘氨胆酸ax =;h = ax.Children;传奇(h ([6 5 1]), {“初始猜测(x ^ 2 - 1)”“迭代”...'新的初始值'},...“位置”,“西北”);
较小的迭代
现在我们分ε通过3并重复上述迭代。融合是再二次。
小量=小量/ 3;而1 VTAU = fnval(Y,colsites);权重= [0 1 0;[2 * VTAU“。零(N-2,1)repmat(ε,正2,1)];1 0 0];colloc =零(N,N);对于J = 1:N colloc(J,:) =权重(J,:)* colmat(3 *(J-1)+(1:3),:);结束coefs = colloc \ [0 VTAU * VTAU + 1 0。]'。Z = SPMAK(节,coefs');fnplt(Z,'B');maxdif = MAX(最大值(ABS(z.coefs-y.coefs)));fprintf中(“maxdif = % g \ n”,maxdif)如果(maxdif <容差),打破,结束%现在重申y = z;结束
maxdif = 0.237937
maxdif = 0.0184488
maxdif = 0.000120467
maxdif = 4.78115e-09
甘氨胆酸ax =;h = ax.Children;图例(h([10 9 5 4]),...{'初始猜测(X ^ 2-1)对小量= 0.1'“迭代”...sprintf (“的小量初始猜测=%.3f”,ε)...“迭代”},“位置”,“西北”);

非常小的ε
对于一个更小的ε,我们只是重复这些计算,除ε每次3点。
对于ee = 1:4节= newknt(z, ninterv+1);休息= knt2brk(节);节= augknt(休息,4,2);n =长度(节)- k;ninterv =长度(减免)1;temp =((优惠(2:ninterv + 1) +优惠(1:ninterv)) / 2);temp = temp([1 1],:) + gauss*diff(break);colsites =临时(:)。';colsites网站= [0,1];colmat = spcol(结,k, brk2knt(位点,3)); intmat = colmat([2 1+(1:(n-2))*3,1+(n-1)*3],:); y = spmak(knots,[0 fnval(z,colsites) 0]/intmat.'); fnplt(y,'C') epsilon = epsilon/3;而1 VTAU = fnval(Y,colsites);权重= [0 1 0;[2 * VTAU“。零(N-2,1)repmat(ε,正2,1)];1 0 0];colloc =零(N,N);对于J = 1:N colloc(J,:) =权重(J,:)* colmat(3 *(J-1)+(1:3),:);结束coefs = colloc \ [0 VTAU * VTAU + 1 0。]'。Z = SPMAK(节,coefs');fnplt(Z,'B');maxdif = MAX(最大值(ABS(z.coefs-y.coefs)));如果(maxdif <容差),打破,结束%现在重申y = z;结束结束甘氨胆酸ax =;h = ax.Children;图例(H([30 29 25 24]),...{'初始猜测(X ^ 2-1)对小量= 0.1'“迭代”...'最初的猜测是= .1/3^j, j=1:5'...“迭代”},“位置”,“西北”);

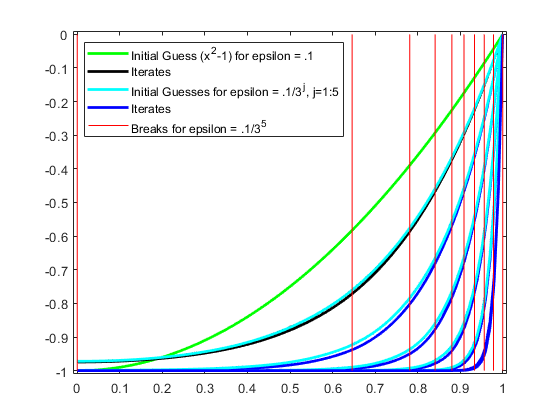
绘制用于最小小量的休息
这里是最终分配休息,显示newknt在这种情况下运作良好。
符= fnbrk(fn2fm(Z,'PP'),'B');bb = repmat(休息,3,1);cc = repmat([0, 1,南],1,长度(休息);情节(bb (:), cc (:),'R');保持从甘氨胆酸ax =;h = ax.Children;图例(H([31 30 26 25 1]),...{'初始猜测(X ^ 2-1)对小量= 0.1'“迭代”...'最初的猜测是= .1/3^j, j=1:5'...“迭代”'的小量符= 0.1 / 3 ^ 5'},“位置”,“西北”);
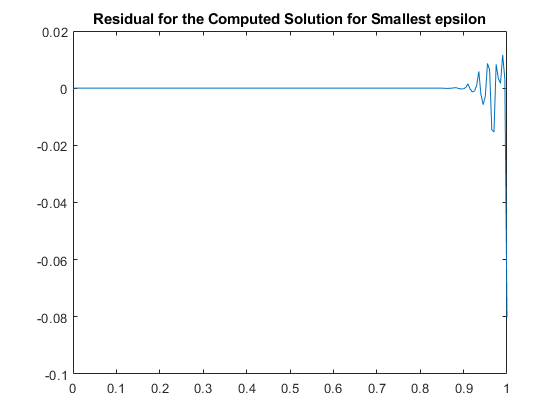
绘制剩余的最小的Epsilon
回想一下,我们正在解决ODE
D^2g(x) + (g(x))^2 = 1 on [0..1]
作为一种检验,我们计算并绘制最小的计算解的残差。这看起来也令人满意。
xx = linspace (0, 1201);plot(xx, 1 - epsilon*fnval(fnder(z,2),xx) - (fnval(z,xx)).^2)“剩余的计算解决方案最小小量”);