并行优化ODE
此示例示出了如何优化的ODE的参数。
当ODE解同时返回时,如何避免两次计算目标函数和非线性约束函数。这个例子比较patternsearch和遗传算法在时间上运行的求解器和解决方案的质量。万博 尤文图斯
您需要一个并行计算工具箱™许可才能使用并行计算。
步骤1.定义问题。
问题是要改变加农炮的位置和角度,以便将炮弹发射到尽可能远的墙外。加农炮初速300米/秒。这堵墙有20米高。如果火炮离墙太近,它就必须以一个太陡的角度发射,并且炮弹不能飞得足够远。如果火炮离墙太远,炮弹也不能飞得足够远。
空气阻力使弹丸速度减慢。阻力与速度的平方成正比,比例常数为0.02。重力作用在弹丸上,使它以9。81 m/s的恒定速度向下加速2。因此,轨迹的运动方程x(t)
在哪里
初始位置x0和初始速度xp0是二维向量。但是,初始高度x0 (2)是0,因此初始位置仅取决于标x0 (1)。初始速度xp0大小为300(初速),所以只取决于初始角度,一个标量。对于一个初始角th,xp0=300 *(COS(TH),SIN(TH))。因此,优化问题只依赖于两个标量,因此它是一个二维问题。使用水平距离和角度作为决策变量。
步骤2。表示ODE模型。
ODE求解器要求你把你的模型表示成一个一阶系统。增加轨迹向量(x1(t),x2(t的时间导数(x”1(t),x”2(t)),以形成一个4 d轨迹向量。在该增强向量而言,差分方程变为
将微分方程写成函数文件,并保存在MATLAB中®路径。
函数[x(3);x(4);x(3);x(4)];% initial,得到f(1)和f(2)正确nrm = norm(x(3:4)) * .02;速度的范数乘以常数f (3) = - x(3) *全国抵抗运动;%的水平加速度f(4) = -x(4)*nrm - 9.81;%的垂直加速度
从离墙30米处以一个角度观察ODE的解PI / 3。

步骤3。使用patternsearch解决。
问题是找到初始位置x0 (1)和初始角x0 (2)最大限度地从弹丸土地墙的距离。因为这是一个最大化问题,尽量减少距离的负(见最大化和最小化)。
使用patternsearch要解决这个问题,您必须提供目标、约束、初始猜测和选项。
这两个文件是目标函数和约束函数。将它们复制到MATLAB路径中的一个文件夹中。
函数f = cannonobjective x0 (x) = (x (1); 0; 300 * cos (x (2)); 300 * sin (x (2)));索尔=数值(@cannonfodder [0, 15], x0);%查找时间t时Y_2(T)= 0zerofnd = fzero (@ (r)德瓦尔(sol r 2), [sol.x (2), sol.x(结束)]);%然后求出此时的x位置f =德瓦尔(sol zerofnd 1);f = - f;距离的%取阴性最大化函数[c,ceq] = cannonconstraint(x)x0 = [x (1), 0; 300 * cos (x (2)); 300 * sin (x (2)));索尔=数值(@cannonfodder [0, 15], x0);如果sol.y (1) < = 0%弹丸不会到达墙C = 20 - sol.y(2,端);其他的%发现当抛射物穿越x = 0zerofnd = fzero (@ (r)德瓦尔(溶胶,r, 1), [sol.x (2), sol.x(结束)]);%然后求高度,然后减去20C = 20 - 德瓦尔(溶胶,zerofnd,2);结束
请注意,目标函数和约束函数设置了它们的输入变量x0到ODE求解器的一个4-D初始点。ODE解算器不会因为炮弹击中了墙而停止。相反,约束函数只是变成正的,表明一个不可行的初值。
初始位置x0 (1)不能高于0,低于-200也是徒劳的。(应该在-20附近,因为在没有空气阻力的情况下,最长的飞行轨迹会以一个角度从-20开始pi / 4的)。类似地,初始角x0 (2)不能低于0,并且不能是上述Pi / 2相。设置边界稍微远离这些初始值:
磅= (-200;0.05);乌兰巴托=(1;π/ 2 . 05);X0 = [-30,PI / 3];%初始猜测
设置UseCompletePoll选项真正。这提供了一个更高质量的解决方案,并允许与并行处理进行直接比较,因为并行计算需要此设置。
选择= optimoptions (“patternsearch”,'UseCompletePoll',真正的);
调用patternsearch来解决这个问题。
抽搐%溶液时间[xsolution、距离、eflag, outpt] = patternsearch (x0, @cannonobjective…[],[]、[][],磅,乌兰巴托,@cannonconstraint选择)toc
优化终止:网格尺寸小于选项。MeshTolerance和约束违反小于选项。约束。xsolution = -28.8123 0.6095 distance = -125.9880 eflag = 1 outpt = function: @cannonobjective problemtype: 'nonlinearconstr' pollmethod: 'gpspositivebasis2n' maxconstraint: 0 searchmethod:[]迭代:5 funccount: 269 meshsize: 8.9125e-07 rngstate: [1x1 struct]消息:'优化终止:网格大小小于选项。运行时间为3.174088秒。
开始关于从壁29米弹丸以一角度0.6095弧度结果在最远的距离,约126微米。报告距离是负的,因为所述目标函数是在壁的距离的负。
可视化解决方案。
x0 = [xsolution (1), 0; 300 * cos (xsolution(2)); 300 *罪(xsolution (2)));索尔=数值(@cannonfodder [0, 15], x0);找到弹丸落地的时间zerofnd = fzero (@ (r)德瓦尔(sol r 2), [sol.x (2), sol.x(结束)]);t = linspace (0, zerofnd);%等次绘图x =德瓦尔(sol t 1);%插入x值y =德瓦尔(sol t 2);%插入y值情节(x, y)上情节([0,0],[0,20],“k”)%画墙包含(的水平距离)ylabel(“弹道高度”)传说(“轨迹”,“墙”,'位置','NW'ylim([0 70])等一下从
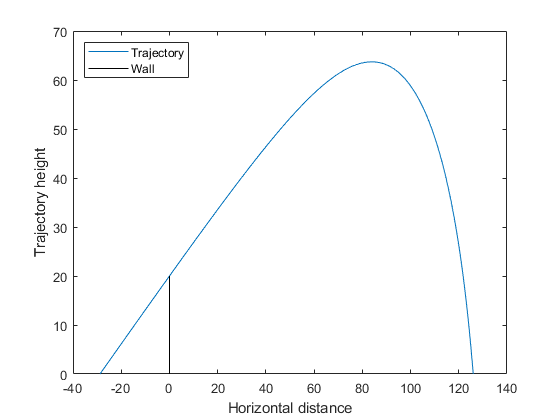
步骤4。避免两次调用昂贵的子例程。
目标函数和非线性约束函数都调用ODE求解器来计算它们的值。在…中使用该技术在同样的功能目标和非线性约束(优化工具箱)避免两次调用求解器。的runcannonfile实现了这项技术。将此文件复制到MATLAB路径中的文件夹中。
函数[x, f, eflag, outpt] = runcannon (x0,选择)如果输入参数个数= = 1未提供选项%OPTS = [];结束xLast = [];最后一个位置ode求解器被调用索尔= [];ODE溶液结构有趣= @objfun;目标函数,嵌套如下cfun = @constr;约束函数,嵌套在下面磅= (-200;0.05);乌兰巴托=(1;π/ 2 . 05);%叫patternsearch[x, f, eflag, outpt] = patternsearch(有趣,x0,[]、[][],[],磅,乌兰巴托,cfun,选择);函数y = objfun (x)如果~ isequal (x, xLast)%检查是否需要计算x0 = [x (1), 0; 300 * cos (x (2)); 300 * sin (x (2)));索尔=数值(@cannonfodder [0, 15], x0);xLast = x;结束%现在计算目标函数弹丸落地时先找到zerofnd = fzero (@ (r)德瓦尔(sol r 2), [sol.x (2), sol.x(结束)]);%然后计算当时的x位置y =德瓦尔(sol zerofnd 1);y = - y;取距离的负数结束函数= constr(x) ceq = [];如果~ isequal (x, xLast)%检查是否需要计算x0 = [x (1), 0; 300 * cos (x (2)); 300 * sin (x (2)));索尔=数值(@cannonfodder [0, 15], x0);xLast = x;结束%现在计算约束函数%首先找到时弹丸杂交x = 0的zerofnd = fzero (@ (r)德瓦尔(溶胶,r, 1), [sol.x (1) sol.x(结束)]);%然后求高度,然后减去20C = 20 - 德瓦尔(溶胶,zerofnd,2);结束结束
重新初始化问题并为调用计时runcannon。
x0 =(-30;π/ 3);tic [xsolution,distance,eflag,outpt] = runcannon(x0,opts);toc
经过时间是2.610590秒。
求解者比以前跑得更快了。如果检查这个解决方案,您会看到输出是相同的。
第5步。并行计算。
通过并行计算来节省更多的时间。首先打开一个并行的工作人员池。
parpool
开始使用“本地”的个人资料...连接到4名工人parpool。ANS =池与属性:连接:真NumWorkers:4集群:本地AttachedFiles:{}的IdleTimeout:30分钟(30分钟剩余)SpmdEnabled:真
设置选项使用并行计算,并重新运行求解。
选择= optimoptions (“patternsearch”选择,“UseParallel”,真正的);x0 =(-30;π/ 3);tic [xsolution,distance,eflag,outpt] = runcannon(x0,opts);toc
运行时间为3.917971秒。
在这种情况下,并行计算较慢。如果检查这个解决方案,您会看到输出是相同的。
步骤6。与遗传算法进行比较。
你也可以尝试用遗传算法来解决这个问题。然而,遗传算法通常是缓慢和不可靠的。
的runcannonga文件调用遗传算法,避免双重评估的ODE求解器。它就像runcannon,但电话遗传算法而不是patternsearch,并检查弹道是否到达壁上。将此文件复制到MATLAB路径中的文件夹中。
函数[X,F,EFLAG,OUTPT] = runcannonga(OPTS)如果输入参数个数= = 1未提供选项%OPTS = [];结束xLast = [];最后一个位置ode求解器被调用索尔= [];ODE溶液结构有趣= @objfun;目标函数,嵌套如下cfun = @constr;约束函数,嵌套在下面磅= (-200;0.05);乌兰巴托=(1;π/ 2 . 05);%叫ga[x, f, eflag, outpt] = ga(乐趣2[]、[][],[],磅,乌兰巴托,cfun,选择);函数y = objfun (x)如果~ isequal (x, xLast)%检查是否需要计算x0 = [x (1), 0; 300 * cos (x (2)); 300 * sin (x (2)));索尔=数值(@cannonfodder [0, 15], x0);xLast = x;结束%现在计算目标函数弹丸落地时先找到zerofnd = fzero (@ (r)德瓦尔(sol r 2), [sol.x (2), sol.x(结束)]);%然后计算当时的x位置y =德瓦尔(sol zerofnd 1);y = - y;取距离的负数结束函数= constr(x) ceq = [];如果~ isequal (x, xLast)%检查是否需要计算x0 = [x (1), 0; 300 * cos (x (2)); 300 * sin (x (2)));索尔=数值(@cannonfodder [0, 15], x0);xLast = x;结束%现在计算约束函数如果sol.y (1) < = 0%弹丸不会到达墙C = 20 - sol.y(2,端);其他的%发现当抛射物穿越x = 0zerofnd = fzero (@ (r)德瓦尔(溶胶,r, 1), [sol.x (2), sol.x(结束)]);%然后求高度,然后减去20C = 20 - 德瓦尔(溶胶,zerofnd,2);结束结束结束
调用runcannonga并行执行。
选择= optimoptions(“遗传算法”,“UseParallel”,真正的);rng默认的再现性% [xsolution,distance,eflag,outpt] = runcannonga(opts) toc
优化终止:适应度值的平均变化小于选项。函数容忍度和约束违反小于选项。约束约束。xsolution = -17.9172 0.8417 distance = -116.6263 eflag = 1 outpt = problemtype: 'nonlinearconstr' rngstate: [1x1 struct]代数:5 funccount: 20212消息:[1x140 char] maxconstraint: 0运行时间为119.630284秒。
的遗传算法解决方案是不如的patternsearch解决方案:117米对126米。遗传算法花了更多的时间:大约120秒而不是5秒。
相关的例子
- 在同样的功能目标和非线性约束(优化工具箱)