具有温度相关性质的传热问题
这个例子说明了如何求解热方程与温度有关的导热系数。算例给出了中心为矩形空腔的矩形砌块的理想热分析。
瞬态传导传热偏微分方程为:
在哪里 是温度, 为物质密度, 比热是多少 为导热系数。 是体内产生的热量,在这个例子中为零。
稳态解:导热系数恒定
创建一个稳态热模型。
thermalmodelS = createpde (“热”,“稳态”);
创建一个二维几何图形,绘制一个矩形的大小块和第二个矩形的大小槽。
r1 =[3 4 -。5。5。5 -。5 -。8 -。8。8。8);r2 =[3 4 -。05。05。05 -。05 -。4 -。4。4。4);gdm = [r1;r2) ';
从第一个矩形中减去第二个矩形,以创建带有槽的块。
g = decsg (gdm,“R1-R2”,(R1的;R2的]“);
将decsg格式转换为几何对象。在模型中包含几何图形。
geometryFromEdges (thermalmodelS g);
用边缘标签显示几何图形。边缘标签将在下面的函数中用于定义边界条件。
图pdegplot (thermalmodelS,“EdgeLabels”,“上”);轴([-。9。9 -。9。9]);标题“显示边缘标签的块几何图形”

把左边的温度设置为100度。在右边的边缘,有规定的热流流出块。顶部和底部边缘以及腔内的边缘都是绝热的,也就是说,没有热量通过这些边缘传递。
thermalBC (thermalmodelS“边缘”6“温度”, 100);thermalBC (thermalmodelS“边缘”, 1“HeatFlux”, -10);
指定材料的导热系数。首先,考虑恒定的导热系数,例如,等于1。之后,考虑导热系数是温度的函数的情况。
thermalProperties (thermalmodelS“ThermalConductivity”1);
创建一个元素不大于0.2的网格。
generateMesh (thermalmodelS“Hmax”, 0.2);图pdeplot (thermalmodelS);轴平等的标题“块与有限元网格显示”
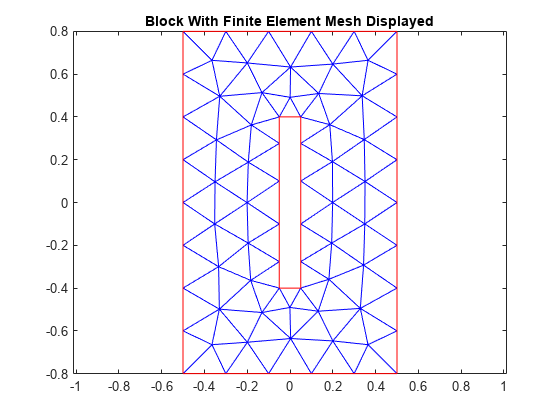
计算稳态解。
R =解决(thermalmodelS);T = R.Temperature;图pdeplot (thermalmodelS,“XYData”T“轮廓”,“上”,“ColorMap”,“热”);轴平等的标题“温度,稳态溶液”
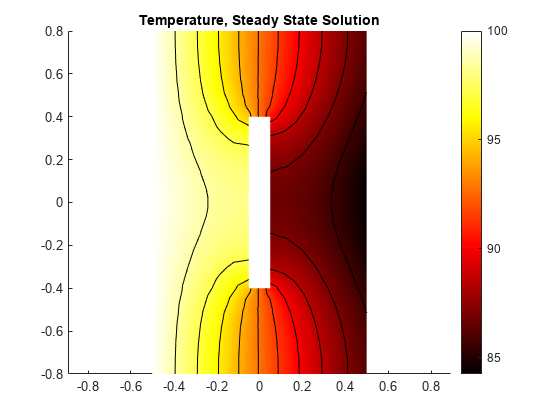
瞬态解决方案:导热系数恒定
创建一个瞬态热模型,包括几何图形。
thermalmodelT = createpde (“热”,瞬态的);r1 =[3 4 -。5。5。5 -。5 -。8 -。8。8。8);r2 =[3 4 -。05。05。05 -。05 -。4 -。4。4。4);gdm = [r1;r2) ';g = decsg (gdm,“R1-R2”,(R1的;R2的]“);geometryFromEdges (thermalmodelT g);
指定材料的热导率、质量密度和比热容。
thermalProperties (thermalmodelT“ThermalConductivity”, 1…“MassDensity”, 1…“SpecificHeat”1);
定义边界条件。在瞬态情况下,左边缘的温度在时间=0时为零,并在0.5秒内上升到100度。你可以找到辅助函数transientBCHeatedBlock下matlab / R20XXx / / pde的主要例子。
thermalBC (thermalmodelT“边缘”6“温度”, @transientBCHeatedBlock);
在右边的边缘,有规定的热流流出块。
thermalBC (thermalmodelT“边缘”, 1“HeatFlux”, -10);
顶部和底部边缘以及腔内的边缘都是绝热的,也就是说没有热量通过这些边缘传递。
创建一个元素不大于0.2的网格。
msh = generateMesh (thermalmodelT,“Hmax”, 0.2);图pdeplot (thermalmodelT);轴平等的标题“块与有限元网格显示”
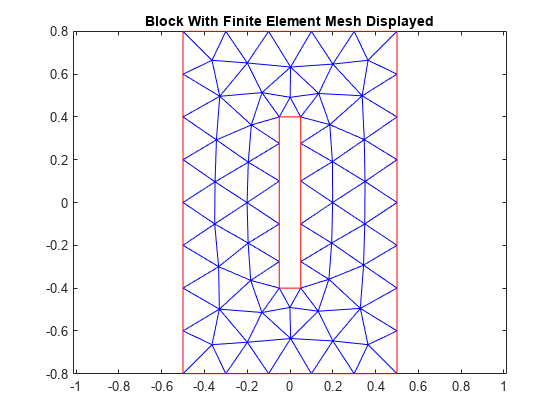
计算暂态解。执行从0到5秒的瞬态分析。工具箱每1秒保存一次解决方案,这样就可以创建作为时间函数的结果图。
tlist = 0: .1:5;thermalIC (thermalmodelT 0);R =解决(thermalmodelT tlist);T = R.Temperature;
有两幅图对理解瞬态分析的结果是有用的。第一个是最后时刻的温度图。第二幅图是物体中一个特定点的温度,在这个例子中靠近右边缘的中心,作为时间的函数。要标识右边缘中心附近的节点,可以方便地定义这个简短的实用函数。
getClosestNode = @(p,x,y) min((p(1,:) - x)^2 + (p(2,:) - y).^2);
调用这个函数来获得靠近右边缘中心的节点。
[~,nid] = getClosestNode(msh)节点,5,0);
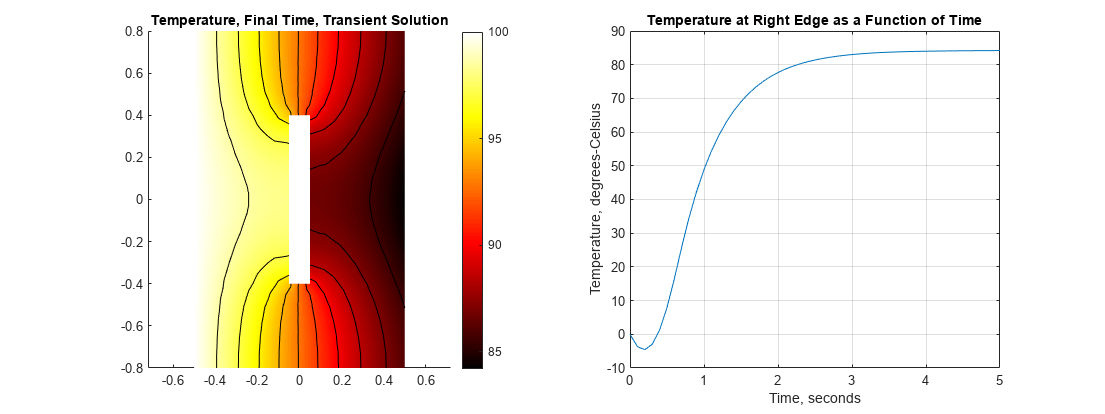
在下面的图中,这两个图形并排显示。此时的温度分布与上述稳态解的温度分布非常相似。在右边,在不到1。5秒的时间里,温度小于零。这是因为热量离开块体的速度比从左边缘到达块体的速度快。在超过三秒的时候,温度基本上达到了稳定状态。
h =图;h。Position = [1 1 2 1].*h.Position;次要情节(1、2、1);轴平等的pdeplot (thermalmodelT“XYData”T(:,结束),“轮廓”,“上”,“ColorMap”,“热”);轴平等的标题温度,最终时间,瞬态解次要情节(1、2、2);轴平等的,情节(tlist T(国家免疫日:));网格在标题“右边缘温度随时间的变化”;包含“时间,秒”ylabel“温度摄氏度”
稳态解:随温度变化的导热系数
材料性质是因变量的函数,这是很常见的。例如,假设导热系数是温度的简单线性函数:
k = @(~,state) 0.3+0.003*state.u;
在这种情况下,变量u是温度。对于这个例子,假设密度和比热不是温度的函数。
thermalProperties (thermalmodelS“ThermalConductivity”、k);
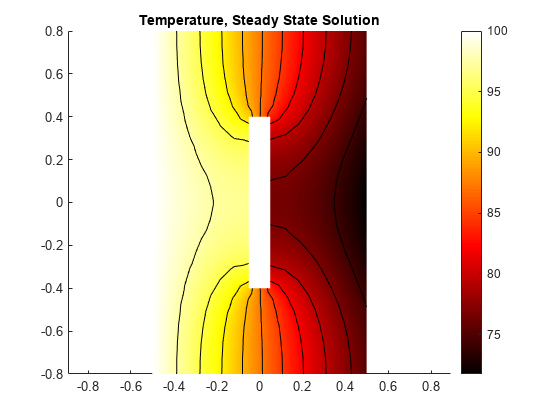
计算稳态解。与等电导率情况相比,右手边的温度更低。这是由于在温度较低的区域导电率较低。
R =解决(thermalmodelS);T = R.Temperature;图pdeplot (thermalmodelS,“XYData”T“轮廓”,“上”,“ColorMap”,“热”);轴平等的标题“温度,稳态溶液”
瞬态解:随温度变化的导热系数
现在用随温度变化的电导率进行瞬态分析。
thermalProperties (thermalmodelT“ThermalConductivity”、钾、…“MassDensity”, 1…“SpecificHeat”1);
使用相同的timespantlist = 0: .1:5对于线性情况。
thermalIC (thermalmodelT 0);R =解决(thermalmodelT tlist);T = R.Temperature;
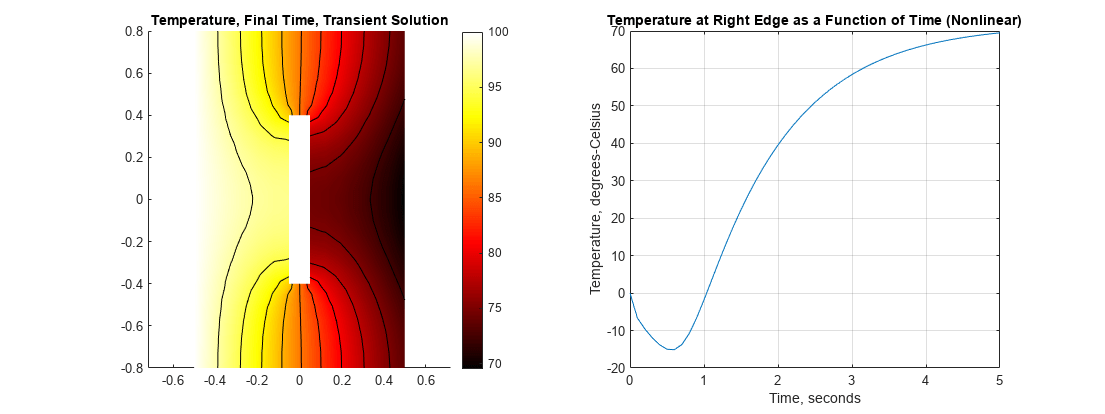
把最后一段时间的温度和右边的温度作为时间的函数画出来。最后时间步的温度图与线性分析的可比图略有不同:右边缘的温度略低于线性情况。温度随时间变化的曲线与线性情况有很大的不同。因为在较低的温度下电导率较低,热量需要更长的时间才能到达砌块的右边缘。在线性情况下,温度在3秒左右基本上是恒定的但在非线性情况下,温度曲线在5秒开始变平。
h =图;h。Position = [1 1 2 1].*h.Position;次要情节(1、2、1);轴平等的pdeplot (thermalmodelT“XYData”T(:,结束),“轮廓”,“上”,“ColorMap”,“热”);轴平等的标题温度,最终时间,瞬态解次要情节(1、2、2);轴平等的情节(tlist(1:尺寸(T, 2))、T (nid:));网格在标题“右边缘温度随时间的变化(非线性)”;包含“时间,秒”ylabel“温度摄氏度”