薄板的非线性传热

打开生活的脚本

这个例子演示了如何对薄板进行传热分析。

板为方形，温度沿底边固定。其他三条边没有热量传递(即它们是绝缘的)。热量通过对流和辐射从板的上下两面传递。因为包括了辐射，所以这个问题是非线性的。这个例子的目的之一是展示如何处理PDE问题中的非线性。

同时进行了稳态和瞬态分析。在稳态分析中，我们感兴趣的是在板达到平衡状态后，板上不同点的最终温度。在瞬态分析中，我们感兴趣的是板内温度作为时间的函数。这个瞬态分析可以回答的一个问题是，平板需要多长时间才能达到平衡温度。

平板传热方程

这块板的平面尺寸是1米乘1米，厚1厘米。由于平板相对于平面尺寸来说相对较薄，可以假设温度在厚度方向上是恒定的;得到的问题是二维的。

假设在给定的环境温度下，板的两面之间发生对流和辐射传热。

由于对流从每个板面在单位面积内传递的热量定义为

$问_{c} ＝ h_{c} （ T - T_{一个} ）$

在哪里 $T_{一个}$ 为环境温度， $T$ 温度是在板表面特定的x和y位置吗 $h_{c}$ 为指定的对流系数。

在单位面积内，由于辐射从每个板面传递的热量定义为

$问_{r} ＝ ϵ σ （ T^{4} - T_{一个}^{4} ）$

在哪里 $ϵ$ 是脸的辐射率和 $σ$ 是斯特凡-玻尔兹曼常数。由于辐射传递的热量与表面温度的四次方成正比，所以这个问题是非线性的。

描述薄板温度的偏微分方程为

$ρ C_{p} t_{z} \frac{\partial T}{\partial t} - k t_{z} \nabla^{2} T + 2 问_{c} + 2 问_{r} ＝ 0$

在哪里 $ρ$ 为材料密度， $C_{p}$ 为比热， $t_{z}$ 为板厚，这两个因素决定了从板两面的传热。

用PDE工具箱所期望的形式重写这个方程是很方便的

$ρ C_{p} t_{z} \frac{\partial T}{\partial t} - k t_{z} \nabla^{2} T + 2 h_{c} T + 2 ϵ σ T^{4} ＝ 2 h_{c} T_{一个} + 2 ϵ σ T_{一个}^{4}$

问题的设置

该板由铜组成，铜具有以下特性:

k = 400;铜热导率%，W/(m-K)ρ= 8960;%铜密度，kg/m^3specificHeat = 386;铜比热% J/(kg-K)厚= . 01;%板厚，单位为米stefanBoltz = 5.670373 e-8;% Stefan-Boltzmann常数，W/(m^2-K^4)hCoeff = 1;%对流系数W/(m^2-K)假定环境温度为300开氏度。ta = 300;工作= 5;板面发射率%

使用单个因变量创建PDE模型。

numberOfPDE = 1;模型= createpde (numberOfPDE);

对于一个正方形，几何和网格很容易定义如下所示。

宽度= 1;身高= 1;

通过给出四个角的x位置和四个y位置来定义正方形。

GDM = [3 4 0 width width 0 0 0 height height]';g = decsg (gdm,“S1 '， (“S1 ') ');

将DECSG几何图形转换为几何对象，这样它就会被附加到PDEModel中

geometryFromEdges(模型中,g);

绘制几何图形并显示边界条件定义中使用的边缘标签。

图;pdegplot(模型,“EdgeLabels”，“上”）;轴([-。1.1 - 1。1 1.1]);标题“显示边缘标签的几何图形”；

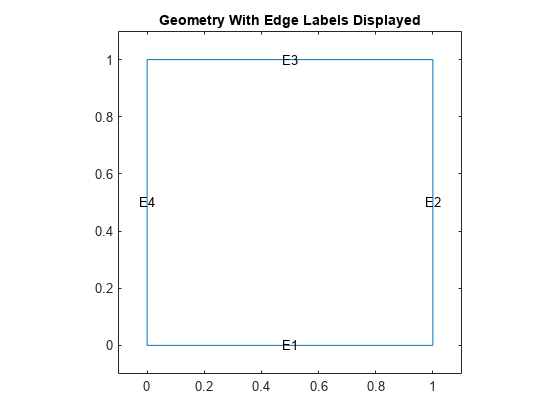
指定系数。通过将上面的方程与PDE工具箱文档中的标量抛物方程进行比较，可以很容易地确定PDE工具箱所需系数的表达式。

c =厚* k;

由于辐射边界条件，“a”系数是温度u的函数，将其定义为MATLAB表达式，以便在分析时对不同的u值进行计算。

a = @(~，state) 2*hCoeff + 2* miss*stefanBoltz*state.u.^3;f = 2*hCoeff*ta + 2* miss*stefanBoltz*ta^4;d = *ρ* specificHeat厚;specifyCoefficients(模型,“米”0,' d '0,“c”c“一个”一个,“f”f);

盘子的下边缘被设置为1000开氏度。

应用边界条件。板的三条边是绝缘的。因为在有限元公式中，诺伊曼边界条件等于零是默认值，所以这些边上的边界条件不需要明确设置。底边1上的所有节点都设置了狄利克雷条件，

applyBoundaryCondition(模型,“边界条件”，“边缘”，1，“u”, 1000);

指定最初的猜测。

setInitialConditions(模型中,0);

在正方形上创建三角形网格，每个方向大约有10个元素。

hmax = 1;%的元素大小msh = generateMesh(模型,“Hmax”, hmax);图;pdeplot(模型);轴平等的标题“带有三角形网格元素的板”包含“x坐标,米”ylabel“坐标,米”

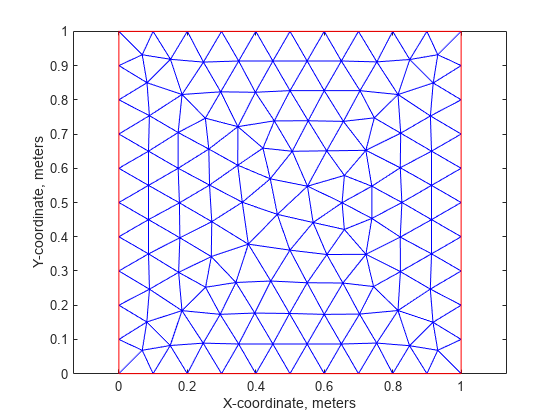
稳态解

因为a和f系数是温度的函数(由于辐射边界条件)，solvepde自动选取非线性求解器求解。

R = solvepde(模型);u = R.NodalSolution;图;pdeplot(模型,“XYData”u“轮廓”，“上”，“ColorMap”，“喷气机”）;标题“板内温度，稳态溶液”包含“x坐标,米”ylabel“坐标,米”轴平等的

p = msh.Nodes;plotAlongY (p, u, 0);标题“温度作为y坐标的函数”包含“坐标,米”ylabel的温度,开尔文

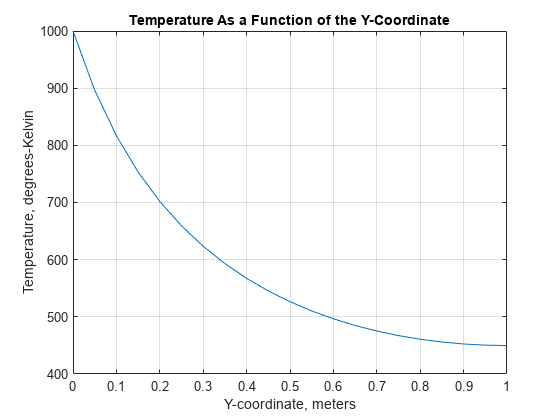
流('板顶边温度= %5.1f度- k \n'，．..u (4));

板块顶部边缘的温度= 449.8度k

临时的解决方案

包括d系数。

specifyCoefficients(模型,“米”0,' d 'd“c”c“一个”一个,“f”f);endTime = 5000;tlist = 0:50: endTime;numNodes =大小(p, 2);

请将所有节点的初始温度设置为环境温度，300k。

情况(1:numNodes) = 300;

将底边E1的初始温度设置为常数BC的值，即1000k。

1000年setInitialConditions(模型,“边缘”1);

设置下列求解器选项。

model.SolverOptions.RelativeTolerance = 1.0 e - 3;model.SolverOptions.AbsoluteTolerance = 1.0的军医;

用实际行动解决问题solvepde．求解器自动选择抛物线求解器来获得解。

R = solvepde(模型、tlist);u = R.NodalSolution;图;:情节(tlist u (3));网格在标题“沿板块顶部边缘的温度与时间的关系”包含“时间,秒”ylabel的温度,开尔文

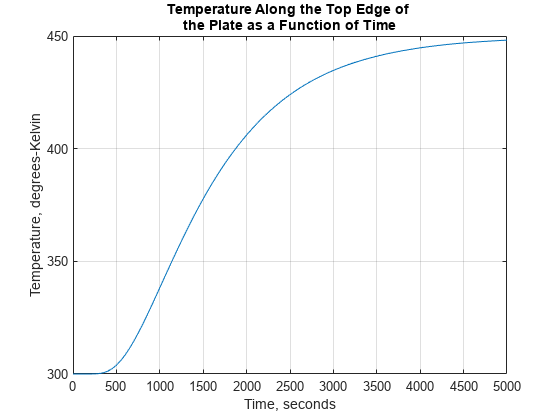
图;pdeplot(模型,“XYData”u(:,结束),“轮廓”，“上”，“ColorMap”，“喷气机”）;标题(sprintf (“极板内温度，瞬态溶液(%d秒)\n”，．..tlist (1)));包含“x坐标,米”ylabel“坐标,米”轴平等的；

流('\n上边缘温度(t=%5.1f secs)=%5.1f degree - k \n'，．..tlist(结束),u (4));

顶部边缘温度(t=5000.0秒)=441.8度- k

总结

在结束时间，由稳态解和瞬态解得到的板内温度曲线非常接近。即在约5000秒后，瞬态解达到稳态值。板上边缘的两种溶液的温度一致在1%以内。万博尤文图斯

偏微分方程工具箱文档

万博1manbetx

尝试MATLAB, Si万博1manbetxmulink和其他产品s manbetx 845

得到审判现在