单位圆盘上的泊松方程

打开生活的脚本

这个例子展示了如何数值求解泊松方程，比较数值解和精确解，并细化网格直到解接近。万博尤文图斯

具有零狄利克雷边界条件的单位圆盘上的泊松方程可以写成 $- Δ u = 1$ 在 $Ω$ , $u = 0$ 上 $δ Ω$ ,在那里 $Ω$ 是单位圆盘。精确解是

$u (x, y) = \frac{1 - x^{2} - y^{2}}{4} 。$

对于大多数偏微分方程，确切的解是不知道的。然而，单位圆盘上的泊松方程有一个已知的精确解，你可以用它来观察当你细化网格时误差是如何减少的。

问题定义

创建PDE模型并包含几何图形。

模型= createpde ();geometryFromEdges(模型、@circleg);

绘制几何图形并显示用于边界条件定义的边缘标签。

图pdegplot(模型,'EdgeLabels',“上”);轴平等的

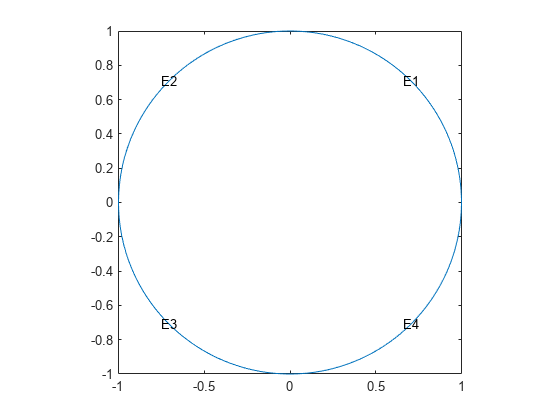
指定所有边上的零狄利克雷边界条件。

applyBoundaryCondition(模型,“边界条件”,“边缘”1: model.Geometry.NumEdges,“u”, 0);

指定系数。

specifyCoefficients(模型,“米”0,' d '0,“c”, 1“一个”0,“f”1);

用粗网格求解和误差

创建具有目标最大元件尺寸0.1的网格。

hmax = 0.1;generateMesh(模型,“Hmax”, hmax);图pdemesh(模型);轴平等的

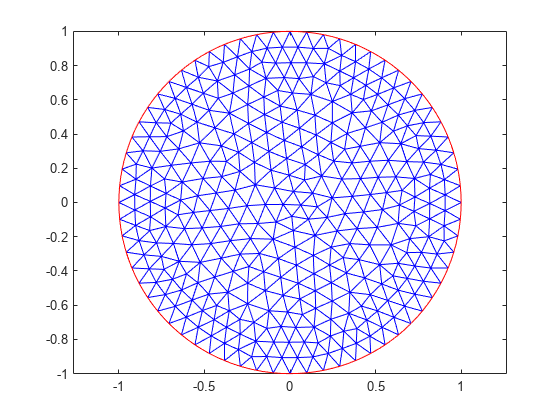
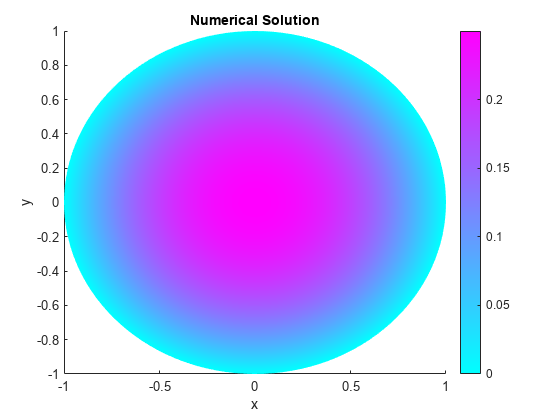
求解偏微分方程并绘制解。

结果= solvepde(模型);u = results.NodalSolution;pdeplot(模型,“XYData”u)标题(的数值解);包含(“x”) ylabel (“y”)

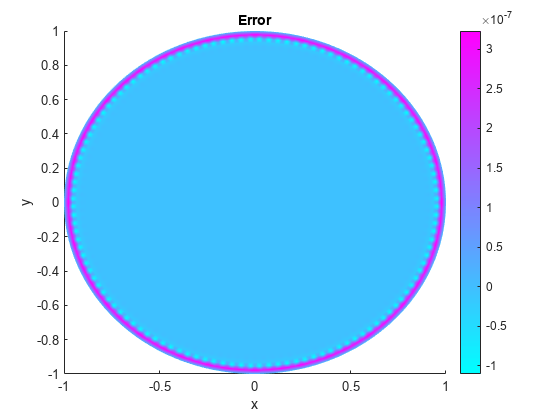
将此结果与精确解析解进行比较，并画出误差。

p = model.Mesh.Nodes;精确= (1 - p(1，:)): ^ 2 - p(2)。^ 2)/ 4;pdeplot(模型,“XYData”，u -准确')名称(“错误”);包含(“x”) ylabel (“y”)

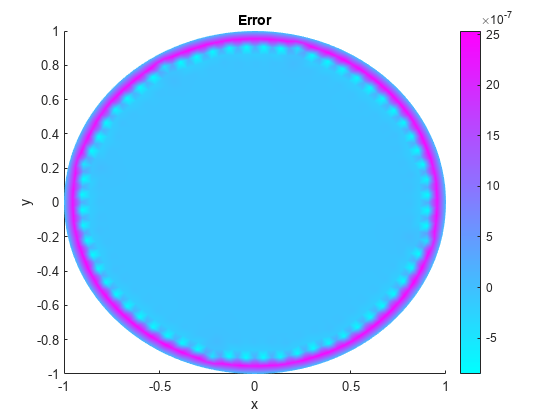
万博尤文图斯精细网格的解决方案和误差

每次迭代细化网格时求解方程，并将结果与精确解进行比较。每一次细化都使Hmax价值。细化网格，直到误差向量的无穷范数小于 ${5 \cdot 10}^{- 7}$ 。

hmax = 0.1;错误= [];呃= 1;而犯错> 5 e -%运行，直到错误<= 5e-7generateMesh(模型,“Hmax”, hmax);%细化网格结果= solvepde(模型);u = results.NodalSolution;p = model.Mesh.Nodes;精确= (1 - p(1，:)): ^ 2 - p(2)。^ 2)/ 4;err = norm(u - exact'，inf);%与精确溶液比较error = [error err];保存错误的历史hmax = hmax / 2;结束

绘制每次迭代的误差向量的无穷范数。误差的值在每次迭代中减小。

情节(错误,“处方”,'MarkerSize'12);甘氨胆酸ax =;斧子。XTick = 1:元素个数(错误);标题(“历史错误”);包含(“迭代”);ylabel (错误的标准);

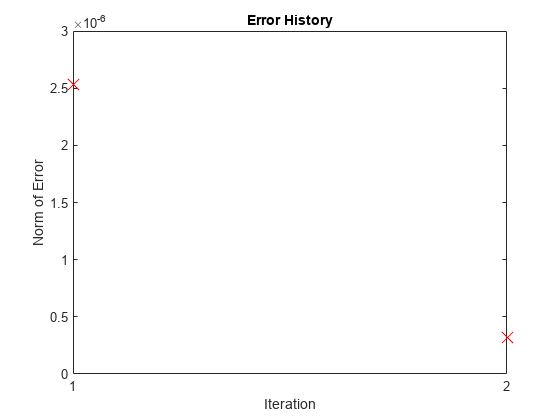
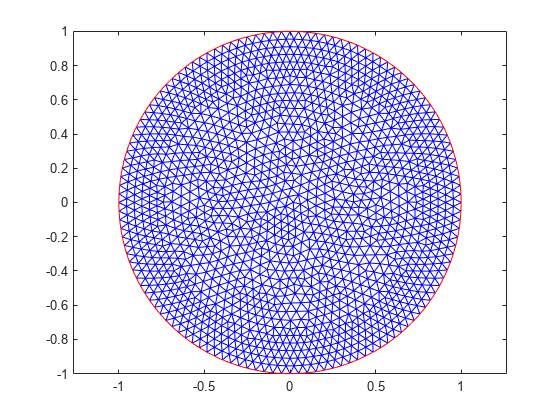
绘制最终网格及其相应的解决方案。

图pdemesh(模型);轴平等的

图pdeplot(模型,“XYData”u)标题(的数值解);包含(“x”) ylabel (“y”)

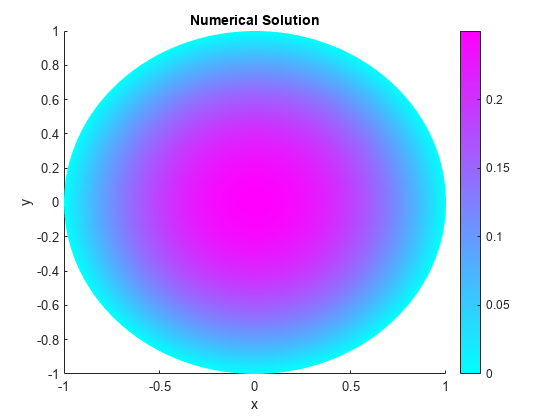
将计算结果与精确解析解进行比较，并画出误差。

p = model.Mesh.Nodes;精确= (1 - p(1，:)): ^ 2 - p(2)。^ 2)/ 4;pdeplot(模型,“XYData”，u -准确')名称(“错误”);包含(“x”) ylabel (“y”)

偏微分方程工具箱文档

万博1manbetx

尝试MATLAB、Sim万博1manbetxulink和其他产品s manbetx 845

得到审判现在