探讨一个模型的求解器雅可比结构

开放模式

该示例展示了如何使用Simulink®来探索求解器雅可比稀万博1manbetx疏模式，以及求解器雅可比稀疏模式与物理系统组件之间的依赖关系之间的联系。使用万博1manbetxSimulink模型模拟放置在自由移动底座上的三个节拍器的同步。

解算雅可比模式

一般来说，Simulink模型的连续部分可以写成:万博1manbetx

$$ & # xA;左\ \{{\开始{数组}{* c {20}} & # xA;{\dot x = f(x,u)} \\ {y = g(x,u)} \\ \end{array}} \right. $$

在哪里 $$ x $$ 连续状态是和吗 $$ u $$ 是输入。 $$ y $$ 是输出。

矩阵:

$J_x = \frac{{\partial f}}{{\partial x}}$

称为系统求解器雅可比矩阵。当使用隐式ODE求解器求解系统方程时， $ J_x $$ 需要时需要计算。例如，一阶ode集合的雅可比矩阵

$$ & # xA;左\ \{{\开始{数组}{* c {20}} & # xA;{\dot x_1 = x_1 x_2} \\ {\点x_2 = x_2} \ \ & # xA; \{数组}}结束\对强生的# xA; $$

是

$J_x = \left[{\begin{array}{*{20}c} {\frac{{\partial f_1}}} {{\partial x_1}} &{\压裂{{\ f部分}}{{\部分x_2}}} \ \ & # xA;{\frac{{\partial f_2}}{{\partial x_1}} &{\压裂{{\部分₂}}{{\部分x_2}}} \ \ & # xA;结束\{数组}}\]= \左右[{\开始{数组}{* c {20}} & # xA;{x_2} &{x_1} \\ 0 & # 38;1 \\ \end{array}} \right] $$$

您可以将解算器的雅可比矩阵转换为布尔稀疏矩阵，方法是将每个非零元素表示为1，将每个始终为零(硬零)的元素表示为0。例如，上面雅可比矩阵对应的布尔矩阵 $ J_x $$ 是:

$$ & # xA; J_ {xp} =左\[{\开始数组{}{* c {20}} & # xA;1 & # 38岁;1 \ \ & # xA;0 & # 38;1 \\ \end{array}} \right]， $$

在哪里 $J_{xp}$ 称为解算器雅可比模式矩阵。

求解器雅可比模式矩阵可由原系统方程直接生成，使用如下规则:

$$ & # xA; J_ {xp}左(i, j) = \ \{{\开始数组{}{* c {20}} & # xA;{1 ~ {\ rm}如果~ {\ rm} x_j ~ {\ rm} ~ {\ rm}明确~ {\ rm} ~ {\ rm}用来计算~ ~ {\ rm} {rm \} \点x_i} \ \ & # xA;{0 ~ {\ rm}否则}\ \ & # xA; \{数组}}结束\对强生的# xA; $$

如你所见，解算器的雅可比模式矩阵实际上表示了状态变量和它们的导数之间的依赖关系。如果计算 $\点x_i$ 需要的价值 $$ x_j $$ ，则存在依赖关系 $\dot x_i \leftarrow x_j$ 而且 $J_{xp} (i,j) = 1$ ．这些依赖关系是由系统的物理性质决定的，因此通过研究求解器雅可比矩阵，您可以探索由模型表示的物理系统的物理结构。万博1manbetxSimulink为用户提供了获取求解器雅可比模式矩阵的api。下面展示了如何访问求解器的雅可比模式，并使用它来研究模型。

模式和依赖:节拍器的同步

同步被定义为振荡物体由于弱相互作用[1]而调整的节奏。荷兰科学家克里斯蒂安·惠更斯(Christiaan Huygens)报告了第一个有科学记录的同步观测，他是钟摆[2]的发明者。惠更斯发现，由椅子支撑的两个钟摆在同一根横梁上，一段时间后会朝着完全相反的方向摆动。万博1manbetx本例中使用的类似设置如图1所示。

图1:在这个例子中使用:三个节拍器在一个移动的基础上

系统建模

该物理系统的模型可分为两部分:

节拍器机制
移动基地

节拍器机制

由图1可得单个节拍器在运动底座上的动力学方程为[3]:

$$ & # xA; \ underbrace {\ ddot \θ}_{角加速度~}+ & # xA; \ underbrace{\压裂{{著}}{J} \罪\θ}_{引力~项}+ & # xA; \ underbrace{左\压裂{b} {J} \[{\离开({\压裂{\θ}{{\θ_r}}} \右)^ 2 - 1}& # xA;正确\]\点\θ}_{阻尼式擒纵机构~和~ ~项}+ \ underbrace& # xA;{\离开({\压裂{{rm \ cosθ\}}{J}} \) \ ddot& # xA; x} _{耦合~惯性~力~项}= 0 ~~~~~~~~~~( eq.1) & # xA; $$

前两个术语描述了一个没有摩擦的简单摆。第三项用于近似擒纵*和节拍器的任何阻尼。这一项增加了角速度 $~\theta < \theta_{0}$ 并将其减小为 $\theta >\theta _{0}$ [3]。最后一项是来自运动底座的耦合效应，用惯性力表示。

移动基地

假设底座的运动是无摩擦的，那么系统的质心不会改变，可以得到:

$$ & # xA; x = - \压裂{m} {{m + 3 m}} r(罪罪\ \θ_1 + \ \θ_2 + \罪# xA; \θ_3),& # xA; $$

在哪里 $$ m $$ 底和的质量是 $$ m $$ 是钟摆的质量。

则式1可改为:

$$ & # xA; \ ddot x = - \压裂{m} {{m + 3 m}}左r \ [{\ ddot \θ_1 \因为\θ_1 - # xA;罪\ \θ_1(点\ \θ_1)^ 2 + \ ddot \θ_2 \ cosθ_2 \ & # xA;罪\ \θ_2(点\ \θ_2)^ 2 + \ ddot \θ_3 \ cosθ_3 \ & # xA;罪\ \θ_3(θ_3 \点\)^ 2}\ ]~~~~~~~~~~( eq.2) & # xA; $$

下面展示了用Simulink实现的上述系统。万博1manbetx该模型包括三个节拍器子系统和运动底座。

图2:节拍器系万博1manbetx统的Simulink模型

对该系统的仿真显示了一个有趣的现象:同步。结果表明，三个初始相位角不同的节拍器最终会相互同步。图3显示了仿真结果。同步的主要原因是将所有节拍器连接在一起的移动底座。这种物理联系可以从每个节拍器的动力学方程中观察到。

此外，这种物理联系也可以从该模型的求解器雅可比模式中观察到。下面的MATLAB®代码展示了如何得到求解器的雅可比矩阵模式。

图3:同步节拍器

得到求解器雅可比模式的步骤

% 1。将求解器设置为任何隐式求解器

set_param(mdl， '求解器'，'ode15s');

% 2。设置求解器的雅可比矩阵方法为稀疏扰动*

set_param(mdl， 'SolverJacobianMethodControl'， ' sparse摄动');

% 3。得到雅可比矩阵的解算器。

J = 万博1manbetxsimulink . solve . getslvrjacobianpattern (mdl);disp('J = ');disp (J);

% 4。在图中显示模式。使用方法J.show

J.show;

% 5。使用给定的州名和其他信息探索模式

stateNames = J.stateNames;disp('stateNames = ');disp (stateNames);

您将看到的结果如下:

J = SlvrJacobianPattern with properties: Jpattern: [8x1 double] numColGroup: 6 colGroup: [8x1 double] stateNames: {8x1 cell} blockHandles:[8x1 double] stateNames = {'sldemo_metro/Moving base/Integrator1'} {'(sldemo_metro/Metronome1/Integrator2).(Theta1)'} {'(sldemo_metro/Metronome3/Integrator2).(Theta2)'} {'(sldemo_metro/Metronome3/Integrator2).(Theta3)'} {'(sldemo_metro/Metronome3/Integrator1).(Thetadot_3)'} {'(sldemo_metro/Metronome2/Integrator1).(Thetadot_2)'} {'(sldemo_metro/Metronome2/Integrator1).(Thetadot_2)'} {'(sldemo_metro/Metronome1/Integrator1).(Thetadot_1)'} {'(sldemo_metro/Metronome1/Integrator1).(Thetadot_1)'} {'(sldemo_metro/Metronome1/Integrator1).(sldemo_metro/Metronome1/Integrator1).(Thetadot_1)'} {' 'sldemo_metro/ Metronome1/Integrator '}}

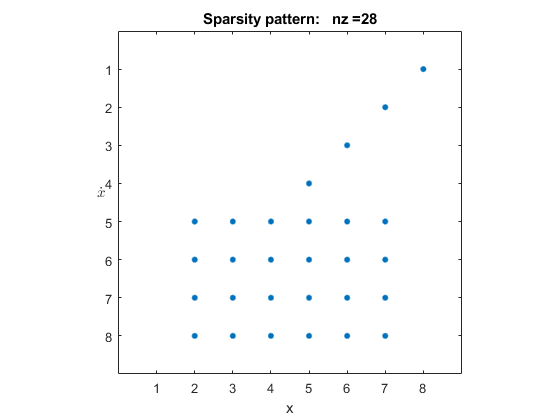
图4:求解器的雅可比模式

求解雅可比模式对象的性质

解算器雅可比矩阵J是一个对象。它包含以下属性:

Jpattern:一个稀疏的mxArray，是雅可比模式。

numColGroup:列组个数。

colgroup:稀疏模式矩阵的列划分。

stateNames:包含每个州的州名的单元格数组。

blockHandles:块句柄的的老板的每一个状态。

求解器雅可比模式的研究

参见图4。首先，该模型的解算器雅可比矩阵稀疏，非零元个数为28。其次，列组数为6;小于状态数8。

第1-4行表示以下依赖项:

$$ & # xA;开始\{数组}{1}& # xA;\dot x_1 \leftarrow x_8 (\dot {baseposition} \leftarrow {basepseed}) \\ \dot {Theta1} \leftarrow x_7 (\dot {Theta1} \leftarrow {Thetadot1}) \\ \dot {Theta2} \leftarrow x_6 (\dot {Theta2} \leftarrow {Thetadot2}) \\ \dot {Theta3} \leftarrow x_5 (\dot {Theta3} \leftarrow {Thetadot3}) \\ 结束\{数组}& # xA; $$

这些关系很清楚，因为速度是位置的导数。第5-8行显示如下关系:

$$ & # xA;开始\{数组}{1}& # xA;\dot x_5 \leftarrow x_{2 - 7} \\ \dot x_6 \leftarrow x_{2 - 7} \\ \dot x_7 \leftarrow x_{2 - 7} \\ \dot x_8 \leftarrow x_{2 - 7} \\ 结束\{数组}& # xA; $$