主要内容

傅科摆的建模

开放模式

这个例子展示了如何建立傅科摆的模型。福柯摆是法国物理学家里昂·福柯的创意。它是为了证明地球是绕轴旋转的。由于地球的轴向旋转，傅科摆的振荡面一整天都在旋转。振荡面以时间间隔T完成一个完整的圆，时间间隔T取决于地理纬度。

福柯最著名的钟摆就安装在巴黎先贤祠里。这是一个28公斤重的金属球，连接在一根67米长的电线上。这个例子模拟了一个位于巴黎地理纬度的67米长的钟摆。

万博1manbetx仿真软件®模型

在Simulink®中解决傅科摆问题最简单的方法是建立一个模型来求解系统的耦合微分方程。万博1manbetx该模型如图1所示。描述傅科摆的方程式如下所示。有关模型的物理原理和这些方程的推导，请参见分析和物理。

$ $ & # xA; \ ddot {x} = 2 \ω\罪{\λ}\点{y} - \压裂{g} {1} x # xA; $ $

$ $ & # xA; \ ddot {y} = - 2 \ω\罪{\λ}\点{x} - \压裂{g} {1} y # xA; $ $

$$ x, y = \mbox{地球上观察者看到的摆bob坐标}$$

$$ ω = mbox{地球绕轴公转的角速度}(rad/sec)$$

$ g = mbox{重力加速度}(m/sec^2

$ L = mbox{摆弦长度}(m)$

$$ = $ mbox{地理纬度}(rad

打开模型

类型sldemo_foucault在MATLAB®命令窗口打开这个模型。该模型将模拟数据记录到变量中sldemo_foucault_output。记录信号有蓝色指示灯。有关更多信息，请参见配置日志信号。

图1:傅科摆模型

初始条件

该模型从sldemo_foucault_data.m文件。这个文件的内容如下面的表1所示。可以直接在MATLAB工作空间中修改仿真参数。摆的初始振幅必须比摆长小，因为微分方程只对小的摆动有效。

表1:初始条件

g = 9.83;%重力加速度(m/sec^2) L = 67;%摆长(m) initial_x = L/100;%初始x坐标(m)%初始y坐标(m)%初始x速度(m/sec)%初始y速度(m/sec)%地球绕轴角速度(rad/sec) =49/180*pi;纬度百分比(rad)

运行仿真

按下模型窗口工具栏上的“Play”按钮，运行模拟。该模拟将使用可变步长僵硬解算器ode23t。它将模拟傅科摆3600秒(你可以改变模拟时间)。模型使用默认的相对容差RelTol = 1 e-6。

图2:傅科摆仿真结果(仿真时间3600秒)

结果

仿真结果如图2所示。仿真计算了摆的x和y坐标，以及摆的x和y速度分量。

钟摆振荡平面在超过24小时内完成360度的扫描。扫描周期是地理纬度的函数λ(见推导分析和物理)．

图3:动画块显示钟摆振荡平面在一小时内旋转多少

运行模拟之后，双击动画块以使结果动画化。

  • 注意:示例的“动画结果”部分需要信号处理工具箱™。双击动画块将导致一个错误，如果它没有安装。在没有信号处理工具箱的情况下，示例的所有其他部分都将正常工作。

的sldemo_foucault_animate.m文件绘制了摆锤在不同时间点的位置。你可以清楚地看到钟摆振荡面是如何旋转的。

  • 注意:如果在较大的相对容差下运行模拟，那么结果在很长一段时间内数值上是不稳定的。确保您使用的是僵硬的变量步长求解器。阅读更多关于刚性问题的数值不稳定性和求解器性能的内容，请参阅“使用刚性模型探索可变步长求解器”。例子。

关闭模式

关闭模式。生成的数据。

分析和物理

本节分析傅科摆并描述其背后的物理原理。摆可以被模拟成一个点质量悬挂在一根长导线上l。钟摆位于地理纬度上λ。使用图4所示的参考系很方便:惯性系I(相对于地球中心)和非惯性系N(相对于地球表面的观测者)。非惯性系由于转动而加速。

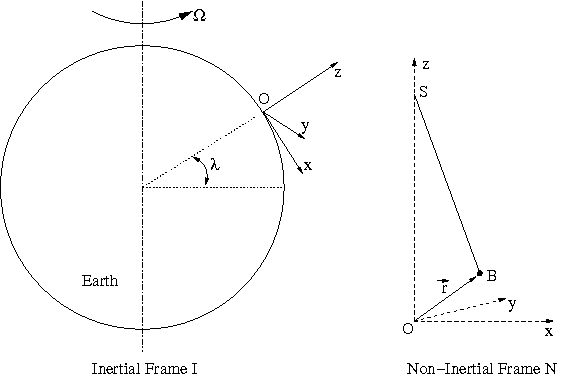
图4:问题的惯性系和非惯性系

点O是非惯性系n的原点。它是地球表面上的一个点，在钟摆的悬浮点之下。非惯性系的选择使z轴远离地球中心并垂直于地球表面。x轴向南，y轴向西。

正如引言中提到的，傅科摆的振荡面是旋转的。振荡面在时间内完成一个完整的旋转刚学步的小孩由下式给出，其中Tday是一天的持续时间(即地球绕地轴一周的时间)。

$T_{rot}=T_{day} \cdot \sin \lambda $$

sin因素需要进一步讨论。人们常常错误地假设，钟摆的振荡面相对于地心固定在惯性系中。这只在北极和南极成立。为了消除这种混乱，考虑点S(见图4)，这里是摆悬挂的地方。在惯性系I中，点S在一个圆上运动。摆锤悬挂在一根定长的金属丝上。简单起见，忽略空气摩擦。在惯性系I中，只有两个力作用在摆锤上，线张力T还有重力成品。

向量r给出了摆锤的位置，B(见图4)。牛顿第二定律表明，作用在物体上的所有力的总和等于质量乘以物体的加速度。

$ m \ddot{{r}} = {T} + {F_g} $

在整个证明过程中，点表示时间导数，箭头表示向量，caps表示酉向量(沿x, y, z轴的i, j, k)。矢量箭头上方的点表示矢量的时间导数。点上方的箭头表示时间导数的矢量。下面是总加速度和径向加速度的区别。

总加速度:

$ $ & # xA; \ ddot {\ overrightarrow {r}} = \压裂{d ^ 2 \ overrightarrow {r}} {d t ^ 2} = & # xA; \压裂{d ^ 2} {d t ^ 2} \离开(x \ mathbf{\帽子{我}}+ y \ mathbf{\帽子{j}} + z \ mathbf{\帽子{k}} \右)& # xA; $ $

径向加速度:

$ $ & # xA; \ overrightarrow {\ ddot {r}} = \ overrightarrow{\离开(\压裂{d r ^ 2} {dt ^ 2} \右)}= & # xA; \ ddot {x} \ mathbf{\帽子{我}}+ & # xA; \ ddot {y} \ mathbf{\帽子{j}} + & # xA; \ ddot {z} \ mathbf{\帽子{k}} & # xA; $ $

重力加速度指向地球中心(负z方向)。

$ $ g = 9.83米/秒^ 2 $ $

$ $ \ overrightarrow {g} = - g \ mathbf{\帽子{k}} $ $

$ $ & # xA; m \ ddot {\ overrightarrow {r}} = & # xA; \ overrightarrow {T}毫克\ mathbf{\帽子{k}} & # xA; $ $

分解加速度项:

$ $ & # xA; \ overrightarrow {r} = & # xA; r_x \ mathbf{\帽子{我}}+ & # xA; r_y \ mathbf{\帽子{j}} + & # xA; r_z \ mathbf{\帽子{k}} & # xA; $ $

$ $ & # xA; \点{\ overrightarrow {r}} = & # xA; \离开(& # xA; \点{r}值\ mathbf{\帽子{我}}+ & # xA; \点{r} _y吗\ mathbf{\帽子{j}} + & # xA; \点{r} _z \ mathbf{\帽子{k}} & # xA; \右)+ & # xA; r_x \点{\ mathbf{\帽子{我}}}+ & # xA; r_y \点{\ mathbf{\帽子{j}}} + & # xA; r_z \点{\ mathbf{\帽子{k}}} & # xA; $ $

单位矢量的时间导数出现是因为非惯性参照系N在空间中旋转。这意味着酉向量i j k在空间中旋转。它们的时间导数如下。是地球绕轴旋转的角速度。标量是角速度的值。矢量是角速度矢量。它的方向由右手定则决定。

$ $ & # xA; \点{\ mathbf{\帽子{我}}}= \ overrightarrow{ω\}\ * \ mathbf{\帽子{我}}& # xA; $ $

$ $ & # xA; \点{\ mathbf{\帽子{j}}} = \ overrightarrow{ω\}\ * \ mathbf{\帽子{j}} & # xA; $ $

$ $ & # xA; \点{\ mathbf{\帽子{k}}} = \ overrightarrow{ω\}\ * \ mathbf{\帽子{k}} & # xA; $ $

重写向量r对的时间导数。

$ $ & # xA; \点{\ overrightarrow {r}} = & # xA; \离开(& # xA; \点{r}值\ mathbf{\帽子{我}}+ & # xA; \点{r} _y吗\ mathbf{\帽子{j}} + & # xA; \点{r} _z \ mathbf{\帽子{k}} & # xA; \右)+ & # xA; \ overrightarrow{ω\}\ * \ overrightarrow {r} = & # xA; \ overrightarrow{\点{r}} + & # xA; \ overrightarrow{ω\}\ * \ overrightarrow {r} & # xA; $ $

类似地，表示向量r的二阶导数。

$ xA; / * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

$ mbox{非惯性系N (x, y, z分量)的加速度}$

$$ = $ mbox{科里奥利加速度}$

$ xA;= $ mbox{由于非惯性系旋转而产生的附加项N}

为了简化这个方程，假设地球的ω非常小。这使得我们可以忽略上面方程的第三项。事实上，第二项(已经比第一项小得多)比第三项大四个数量级。这将方程简化为以下形式:

$ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $， $ x $

牛顿第二定律可以写成并分解为x、y、z分量:

$ mg\mathbf{\hat{k}} - 2 m \Omega} \times {dot{r}}

$ $ & # xA; m \ ddot {x} = T_x + 2 mω\ \点{y} \罪{\λ}& # xA; $ $

$ $ & # xA; m \ ddot {y} = T_y - 2 mω\ \离开(\点{x} \罪{\λ}+ \点{z} \因为{\λ}\右)& # xA; $ $

$ $ & # xA; m \ ddot {z} = T_z毫克+ 2 mω\ \点{y} \因为{\λ}& # xA; $ $

振荡的角振幅很小。因此，我们可以忽略垂直速度和垂直加速度(z点和z双点)。弦张力分量可以用小角度近似表示，这也大大简化了问题，使之成为二维的(见下文)。

$T_z = mg - 2m\Omega \dot{y} \cos{\lambda} \simeq mg$$

$ $ T_x = - t \压裂{x} {L} $ $

$ $ T_y = - t \压裂{y} {L} $ $

$ $ T_z = T \压裂{L-z} {1} \ simeq T $ $

特性微分方程

最后，这个问题的物理性质可以用下面给出的耦合方程组来描述。x和y坐标表示在地球上观测者所看到的摆锤的位置。

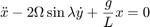
$ $ & # xA;ω\ ddot {x} - 2 \ \罪{\λ}\点{y} + \压裂{g} {1} x = 0 & # xA; $ $

$ $ & # xA;ω\ ddot {y} + 2 \ \罪{\λ}\点{x} + \压裂{g} {1} y = 0 & # xA; $ $

分析解决方案(近似)

下面是傅科摆问题的解析解。不幸的是，它并不准确。如果你试着把解析解代入微分方程，未消项的平方仍然存在。但是，因为很小，我们可以忽略未消项。

如果x+ i + cdot y = mbox{(复数)}，则表示x+ i + cdot y = mbox{(复数)}

$ $ \ ddot{\埃塔}+(2我罪\ω\{\λ})\点{\埃塔}+ \压裂{g}{1} \η= 0 $ $

$ $ \ \时间离开(c₁e ^{我大概{g / L} \ t} + c₂e ^ {- i \ sqrt {g / L} t} \右)& # xA; e ^{我罪\ωt \{\λ}}$ $

$$ C_1, C_2 \mbox{are complex integration constants}

实际的微分方程组是不对称的

在推导过程中，涉及的平方项被忽略。这导致了微分方程中的xy对称。如果考虑到的平方项，微分方程组就变成不对称的(见下文)。

$ $ & # xA; \ ddot {x} - 2ω\ \罪{\λ}\点{y} +(\压裂{g}{1} -罪\ω^ 2 \ ^ 2{\λ})x = 0 & # xA; $ $

$ $ & # xA; \ ddot {y} + 2 \ω\罪{\λ}\点{x} +(\压裂{g}{1} - \ω^ 2)y = 0 & # xA; $ $

你可以很容易地修改当前的傅科摆模型来解释不对称微分方程。只需编辑包含的相应的增益块g / L并添加必要的表达式。这一变化将对数值结果进行非常小的整体修正。

万博1manbetx仿真软件文档

万博1manbetx

基于模型的嵌入式控制系统设计

基于模型的嵌入式控制系统设计

下载白皮书