用主成分分析拟合正交回归
这个例子展示了如何使用主成分分析(PCA)来拟合线性回归。PCA最小化了数据到拟合模型的垂直距离。这就是所谓的正交回归或总最小二乘的线性情况,当预测器和响应变量之间没有自然区别,或所有变量都有误差时,这是合适的。这与通常的回归假设相反,即预测变量是精确测量的,只有响应变量有误差成分。
例如,给定两个数据向量x和y,您可以拟合一条线,使每个点(x(i), y(i))与这条线的垂直距离最小。更一般地说,有了p个观测变量,你就可以在p维空间中容纳一个r维超平面(r < p)。r的选择相当于选择保留在PCA中的分量的数量。它可能是基于预测错误,也可能只是一种实用的选择,以便将数据减少到可管理的维度数量。
在这个例子中,我们通过三个观测变量的一些数据拟合一个平面和一条直线。对于任意数量的变量和模型的任意维度,做同样的事情是很容易的,尽管在更高维度中可视化适合显然不是很简单。
将飞机与3-D数据相匹配
首先,我们为示例生成一些三元正态数据。其中两个变量是相当紧密相关的。
rng (5“旋风”);X = mvnrnd([0 0 0], [1.2 .7];2 1 0;1:8 0 1], 50);plot3 (X (: 1) X (:, 2), X (:, 3),“波”);网格在;maxlim = max (abs (X (:))) * 1.1;轴([-maxlim maxlim -maxlim maxlim]);轴广场视图(9、12);
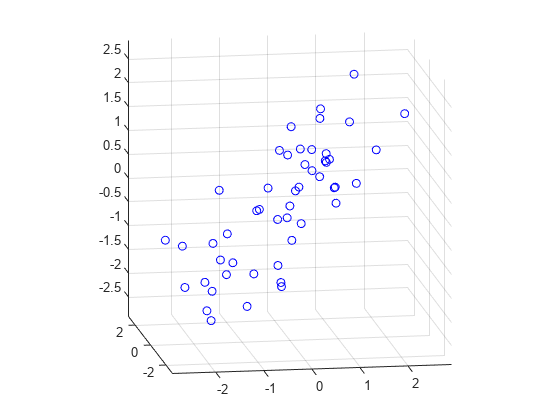
接下来,我们使用PCA将平面与数据匹配。前两个主分量的系数定义了构成平面基的向量。第三个PC正交于前两个,它的系数定义了平面的法向量。
[多项式系数,分数,根]= pca (X);基础=多项式系数(:1:2)
基础=3×20.6774 -0.0790 0.2193 0.9707 0.7022 - 0.22269
正常=多项式系数(:3)
正常=3×10.7314 -0.0982 -0.6749
这就是最合适的了。但让我们更仔细地看看结果,并将其与数据绘制在一起。
因为前两个部分解释了二维数据中尽可能多的方差,所以平面是对数据最好的二维线性逼近。同样地,第三个成分解释了数据中最小的变化量,它是回归中的误差项。来自PCA的潜在根(或特征值)定义了每个分量的解释方差量。
pctExplained = roots' ./ sum(根)
pctExplained =1×30.6226 0.2976 0.0798
主分量分数的前两个坐标给出了每个点在平面坐标系中的投影。为了得到拟合点在原坐标系下的坐标,我们将每个PC系数向量乘以相应的分数,再加上数据的均值。残差就是原始数据减去拟合点。
(氮、磷)= (X)大小;meanX =意味着(X, 1);Xfit = repmat (meanX n 1) +得分(:1:2)*多项式系数(:,1:2)”;残差= X - Xfit;
其中每个拟合点所满足的拟合平面方程Xfit,是([x1 x2 x3] - meanX)*normal = 0.平面通过这个点meanX,它到原点的垂直距离是meanX *正常.从每一点到这里的垂直距离X即残差的范数,是每个中心点与平面法线的点积。拟合平面使误差平方和最小化。
错误= abs((X - repmat(meanX,n,1))*normal);上交所=总和(错误。^ 2)
上交所= 15.5142
为了可视化拟合,我们可以画出平面,原始数据,以及它们在平面上的投影。
[xgrid, ygrid] = meshgrid (linspace (min (X(: 1))马克斯(X (: 1)), 5),...linspace (min (X(:, 2))马克斯(X (:, 2)), 5));zgrid = (1/normal(3)) .* (meanX*normal - (xgrid.*normal(1) + ygrid.*normal(2)));h =网(xgrid ygrid zgrid,“EdgeColor”(0 0 0),“FaceAlpha”, 0);持有在> = (X-repmat(meanX,n))*normal < 0);下面= ~以上;nabove =(上图)之和;X1 = [X(上,1)Xfit(上,1)nan*ones(上,1)];X2 = [X(上,2)Xfit(上,2)nan*ones(上,1)];X3 = [X(上,3)Xfit(上,3)nan*ones(上,1)];plot3 (X1, X2, X3 ',“- - -”X(上图,1)X(上图,2),X(上图,3),“o”,“颜色”, [0 0]);nbelow =(下图)之和;X1 = [X(below,1) Xfit(below,1) nan*ones(nbelow,1)];X2 = [X(below,2) Xfit(below,2) nan*ones(nbelow,1)];X3 = [X(below,3) Xfit(below,3) nan*ones(nbelow,1)];plot3 (X1, X2, X3 ',“- - -”X(下图1)X(下面,2),X(下面,3),“o”,“颜色”, (1 0 0));持有从maxlim = max (abs (X (:))) * 1.1;轴([-maxlim maxlim -maxlim maxlim]);轴广场视图(9、12);
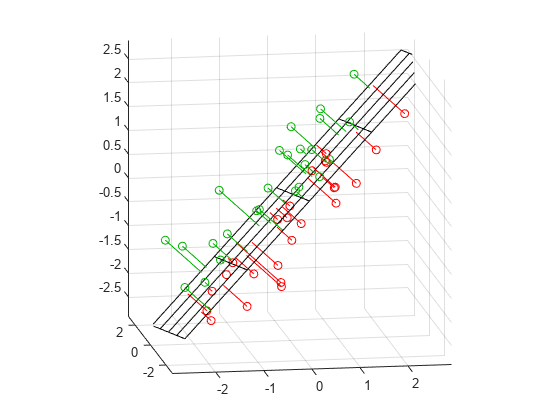
绿色的点在平面上方,红色的点在平面下方。
3-D数据拟合线
对数据拟合一条直线甚至更简单,而且由于PCA的嵌套属性,我们可以使用已经计算过的组件。定义直线的方向向量由第一个主分量的系数给出。第二个和第三个pc正交于第一个,它们的系数定义了垂直于直线的方向。描述这条直线最简单的方程是meanX + t * dirVect,在那里t参数化沿直线的位置。
dirVect =多项式系数(:1)
dirVect =3×10.6774 0.2193 0.7022
主分量分数的第一个坐标给出了每个点在直线上的投影。与二维拟合一样,PC系数向量乘以分数给出了原始坐标系中的拟合点。
Xfit1 = repmat (meanX n 1) +得分(:1)*多项式系数(:1)';
画出直线,原始数据,以及它们在直线上的投影。
t = [min(分数(:1))。2,马克斯(得分(:1))+ 2];endpts = [meanX + t(1)*dirVect';meanX + t (2) * dirVect '];plot3 (endpts (: 1) endpts (:, 2), endpts (:, 3),“k -”);X1 = [X(:,1) Xfit1(:,1) nan*ones(n,1)];X2 = [X(:,2) Xfit1(:,2) nan*ones(n,1)];X3 = [X(:,3) Xfit1(:,3) nan*ones(n,1)];持有在plot3 (X1, X2, X3 ',“b -”X (: 1) X (:, 2), X (:, 3),“波”);持有从maxlim = max (abs (X (:))) * 1.1;轴([-maxlim maxlim -maxlim maxlim]);轴广场视图(9、12);网格在
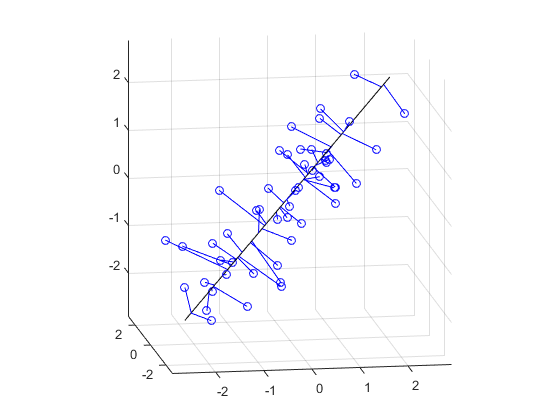
虽然这幅图中的许多投影看起来都不垂直于这条线,但这只是因为我们在二维中绘制3d数据。在一个生活MATLAB®在图形窗口中,您可以交互地将图旋转到不同的透视图,以验证投影确实是垂直的,并更好地感受线与数据的吻合程度。

