拟合自定义单变量分布
这个例子展示了如何使用Statistics和Machine Learning Toolbox™函数大中型企业使自定义分布适合于单变量数据。
使用大中型企业,您可以计算最大似然参数估计,并估计它们的精度,对于许多种类的分布,除了Toolbox提供特定拟合函数的分布之外。
要做到这一点,你需要定义使用一个或多个M功能的分布。在最简单的情况下,你可以编写代码来计算要符合分布的概率密度函数(PDF),和大中型企业会做其余大部分的工作适合你。这个例子介绍这些情况。在截尾数据的问题,你还必须编写代码来计算累积分布函数(CDF)或生存函数(SF)。在一些其他的问题,它可能是有利的,以限定对数似然函数(LLF)本身。本实施例中的第二部分,安装自定义单变量分布,第2部分,涵盖后两种情况。
自定义分布的拟合:一个零截断泊松的例子
计数数据通常使用泊松分布建模,您可以使用统计学和机器学习工具箱函数poissfit来拟合泊松模型。然而,在某些情况下,数据中不会记录为零的计数,因此,由于这些“缺失的零”,拟合泊松分布并不简单。这个例子将展示如何使用函数将泊松分布拟合到零截尾数据大中型企业.
对于本例,我们将使用零截断泊松分布的模拟数据。首先,我们生成一些随机泊松数据。
rng (18,“旋风”);n = 75;λ= 1.75;x = poissrnd(λ,n, 1);
接下来,我们从数据中删除所有的零来模拟截断。
X = X(X> 0);长度(x)
ans = 65
这是这些模拟数据的直方图。请注意,除了没有零之外,这些数据看起来很像泊松分布。我们将用一个分布来拟合它与正整数上的泊松分布相同,但在0处没有概率。这样,我们可以估计泊松参数lambda,同时考虑“缺失零”。
嘘(x,[0:1:马克斯(x) + 1]);
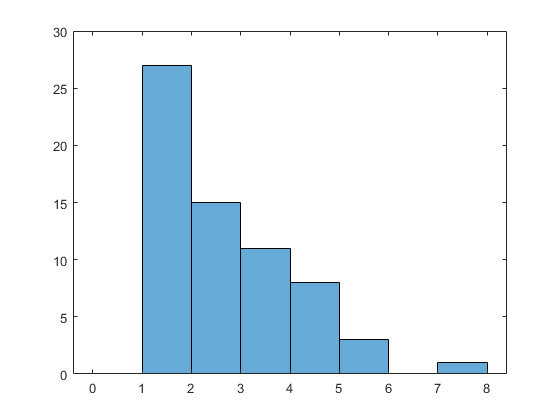
第一步是用概率函数(PF)定义零截断泊松分布。我们将创建一个函数,在给定泊松分布的均值参数lambda值的情况下,计算x中每个点的概率。零截断泊松的PF就是通常的泊松PF,经过重正化使其和为1。在零截断的情况下,重正化仅为1-Pr{0}。为PF创建函数的最简单方法是使用匿名函数。
Pf_truncpoiss = @(x,lambda) poisspdf(x,lambda) ./ (1-poisscdf(0,lambda));
为了简单起见,我们假设给这个函数的所有x值都是正整数,不需要检查。错误检查,或者更复杂的发行版,可能需要不止一行代码,这意味着函数应该在一个单独的文件中定义。
下一步是为参数lambda提供一个合理的粗略的初步猜测。这里,我们用样本均值。
开始=意味着(x)
启动= 2.2154
我们提供大中型企业使用'pdf'参数对数据和匿名函数进行处理。(泊松是离散的,所以这实际上是一个概率函数,而不是PDF。)因为泊松分布的平均参数必须是正的,我们也指定了的下界。大中型企业返回lambda的最大似然估计,并可选地返回参数的近似95%置信区间。
[lambdaHat, lambdaCI] =大中型企业(x,“pdf”pf_truncpoiss,“开始”开始,'降低', 0)
lambdaHat = 1.8760
lambdaCI =2×11.4990 - 2.2530
注意,参数估计比样本均值要小。这是应该的,因为最大似然估计解释了数据中不存在的缺失零。
我们也可以计算lambda的标准误差估计,使用返回的大样本方差近似mlecov.
阿瓦尔= mlecov(lambdaHat,X,“pdf”,pf_truncpoiss);标准错误= SQRT(阿瓦尔)
标准错误= 0.1923
为分布函数提供附加值:截断的正态示例
有时也会发生连续数据被截断的情况。例如,由于收集数据的方式的限制,大于某个固定值的观测值可能不会被记录下来。这个例子将展示如何使用函数将正态分布拟合到截断的数据上大中型企业.
对于这个例子,我们模拟的数据来自截断的正态分布。首先,我们生成一些随机正态数据。
n = 75;μ= 1;σ= 3;x = normrnd(μ、σ,n, 1);
接下来,我们删除所有超出截断点xTrunc的观测值。在整个示例中,我们假设xTrunc是已知的,不需要估计。
xTrunc = 4;x = x(x < x trunc);长度(x)
ans = 64
这是这些模拟数据的直方图。我们将适合将它们与一个分布等同于正常对于x 与前面的示例一样,我们将通过其PDF定义截断的正态分布,并创建一个函数来计算x中每个点的概率密度,给定参数mu和sigma的值。在截断点固定和已知的情况下,被截断的法线的PDF只是普通的法线PDF,被截断,然后重新规格化,以便它集成为1。重正化就是在xTrunc处计算的CDF。为了简单起见,我们假设所有的x值都小于xTrunc,而不进行检查。我们将使用一个匿名函数来定义PDF。 截断点xTrunc没有被估计,因此它不在PDF函数的输入参数列表中的分布参数中。xTrunc也不是数据向量输入参数的一部分。使用匿名函数,我们可以简单地引用已经在工作空间中定义的变量xTrunc,不需要担心将它作为附加参数传入。 我们还需要为参数估计提供一个粗略的初始猜测。在这种情况下,由于截断不是太极端,样本均值和标准偏差可能会工作得很好。 我们提供 注意,mu和sigma的估计要比样本均值和标准差大得多。这是因为模型拟合已经解释了分布的“缺失”上尾。 我们可以计算一个近似协方差矩阵的参数估计使用 一些数据集显示出双峰,甚至多模态,并拟合标准分发这样的数据通常是不恰当的。然而,简单的单峰分布的混合通常可以建模这样的数据非常好。事实上,它甚至有可能以得到解释,以在混合物中各成分的来源,基于应用程序特定的知识。 在本例中,我们将对一些模拟数据拟合两种正态分布的混合物。这种混合可以用以下构造定义来描述,以生成一个随机值: 对于本例,我们将从混合的Student的t分布生成数据,而不是使用我们拟合的相同模型。这是你在蒙特卡罗模拟中可能会做的事情,以测试拟合方法对偏离拟合模型假设的稳健程度。然而,在这里,我们只适合一个模拟数据集。 与前面的示例一样,我们将通过创建一个计算概率密度的函数来定义模型。两个正态分量的混合PDF只是两个正态分量的PDF的加权和,由混合概率加权。这个PDF非常简单,可以使用匿名函数创建。该函数接受6个输入:一个用于评估PDF的数据向量,以及分布的5个参数。每个分量都有其均值和标准差的参数;混合概率是5。 我们还需要对参数进行初步猜测。一个模型的参数越多,合理的起点就越重要。对于这个例子,我们将从相同的正态数混合物(p = 0.5)开始,集中在数据的两个四分之一处,具有相同的标准差。标准偏差的起始值来自混合物的方差公式,该公式由每个成分的均值和方差表示。 最后,我们需要指定的零和一个用于混合概率界限,以及标准差降低的零界限。向量被设置为+ - Inf或-Inf边界的其余元件,以指示没有限制。 自定义分布的默认值是200次迭代。 属性创建的选项结构覆盖该默认值 看来,最终的迭代收敛只在结果的最后几位重要的。然而,它始终是一个好主意,以确保收敛已经达到。 最后,我们可以绘制拟合密度与原始数据的概率直方图,以直观地检查拟合情况。 当收集数据,每个观测在与不同的精度或可靠性制成,有时会发生。例如,如果几个实验者各进行一些相同数量的独立测量,但每次只报告他们的平均测量,每个报告的数据点的可靠性将取决于走进它的原始观测次数。如果原始数据不可用,他们分布的估计必须考虑的事实是可用的数据,平均值,各有不同的差异。这种模式实际上有最大似然参数估计的明确的解决方案。然而,为了说明的目的,我们将使用 假设我们有10个数据点,每个数据点实际上是1到8个观测值的平均值。这些原始的观测数据是不存在的,但是我们知道每个数据点有多少。我们需要估计原始数据的平均值和标准差。 每个数据点的方差成反比进入它,观测的数量,以便我们将使用1 / m至加权每个数据点的方差中的最大似然配合。 在我们所拟合的模型中,我们可以通过它的PDF来定义分布,但是使用日志PDF更自然一些,因为普通的PDF是这种形式的 和 日志PDF函数来计算给定值mu和sigma的日志x中的每个点的概率密度的。它也将需要考虑不同的方差的权重。不同于以往的例子中,这个分布函数是不是一个班轮多了几分复杂,最明确的书面作为它自己的文件一个单独的函数。因为日志PDF功能需要观察算作额外的数据,来完成这个配合是最直接的方法是使用嵌套函数。 我们已经为一个名为 在 我们需要为参数估计提供了一个粗略的猜测。在这种情况下,未加权样本均值和标准差应该是好,这就是 为了拟合模型,我们运行拟合函数。 注意mu的估计小于样本均值的三分之二。这是应该的:估计值受最可靠的数据点的影响最大,也就是那些基于最大量原始观测的数据点。在这个数据集中,那些点倾向于从未加权的样本均值拉下估计。 在最大似然估计中,参数的置信区间通常是用估计量分布的大样本正态近似来计算的。这通常是一个合理的假设,但在小样本容量的情况下,有时通过转换一个或多个参数来改进正态逼近是有利的。在这个例子中,我们有一个位置参数和一个比例参数。尺度参数通常转换成对数,我们这里用。首先,我们将创建一个新的日志PDF函数,然后使用该参数重新计算估计。 新的日志PDF函数被创建为函数中的嵌套函数 请注意, 由于参数化使用对数(sigma),我们必须转换回原始尺度,以得到sigma的估计和置信区间。请注意,mu和sigma的估计与第一次拟合时相同,因为最大似然估计对参数化是不变的。嘘(x, (-10: .5:4));
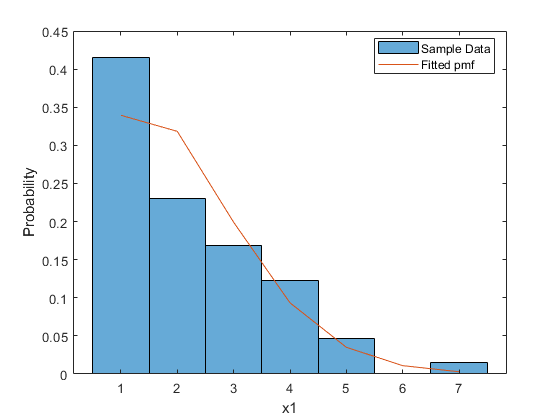
pdf_truncnorm = @(x,mu,sigma) normpdf(x,mu,sigma) ./ normcdf(xTrunc,mu,sigma);
开始= [平均(x)中,STD(x)]的
开始=1×20.2735 - 2.2660
大中型企业使用'pdf'参数对数据和匿名函数进行处理。因为必须是正的,我们也指定了参数的下界。大中型企业返回mu和sigma作为单个向量的最大似然估计,以及两个参数的近似95%置信区间矩阵。[paramEsts, paramCIs] =大中型企业(x,“pdf”pdf_truncnorm,“开始”开始,'降低'(从0))
paramEsts =1×20.9911 - 2.7800
paramCIs =2×2-0.1605 1.9680 2.1427 3.5921
mlecov.这种近似在大样本下通常是合理的,估计的标准误差可以用对角线元素的平方根来近似。acov = mlecov(paramEsts, x,“pdf”pdf_truncnorm)
acov =2×20.3452 0.1660 0.1660 0.1717
stderr =√诊断接头(acov))
stderr =2×10.5876 - 0.4143
拟合一个更复杂的分布:两个正态的混合
首先,抛硬币偏置。如果它的土地头,从平均mu_1和标准偏差sigma_1正态分布挑选随机的值。如果硬币落地的尾巴,从平均mu_2和标准偏差sigma_2正态分布挑选随机的值。
X = [trnd(20,1,50) trnd(4, 1100)+3];嘘(x, -2.25: .5:7.25);
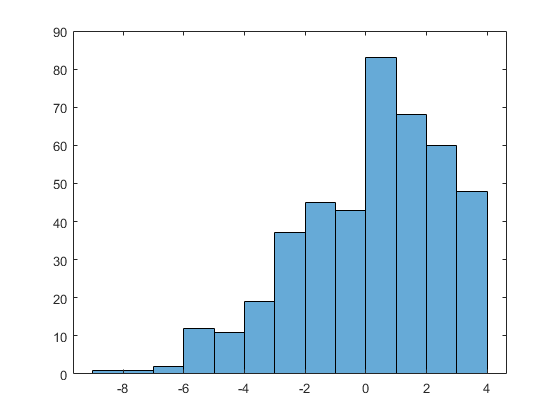
pdf_normmixture = @ (x p、mu1 mu2, sigma1, sigma2)...p * normpdf (x, mu1 sigma1) + (1 - p) * normpdf (x, mu2 sigma2);
pStart = 5;muStart =分位数(x,[。25。)
muStart =1×20.5970 - 3.2456
sigmaStart = sqrt(var(x) - .25*diff(muStart).²)
sigmaStart = 1.2153
start = [pStart muStart sigmaStart sigmaStart]; / /开始
磅= [0 -Inf -Inf 0 0];UB = [1 Inf文件Inf文件Inf文件Inf文件]。paramEsts大中型企业的(x) =“pdf”pdf_normmixture,“开始”开始,...'降低'磅,'上',UB)
警告:最大似然估计没有收敛。迭代限制超标。
paramEsts =1×50.3523 0.0257 3.0489 1.0546 1.0629
statset (“mlecustom”)
ans =结构体字段:Display: 'off' MaxFunEvals: 400 MaxIter: 200 TolBnd: 1.0000e-06 TolFun: 1.0000e-06 TolTypeFun: [] TolX: 1.0000e-06 TolTypeX: [] GradObj: 'off' Jacobian:[]衍生步骤:6.0555e-06 FunValCheck: 'on' Robust: []
statset函数。还增加了函数的求值限制。选项= statset(“麦克斯特”,300,'MaxFunEvals', 600);paramEsts大中型企业的(x) =“pdf”pdf_normmixture,“开始”开始,...'降低'磅,'上',UB,'选项'选项)
paramEsts =1×50.3523 0.0257 3.0489 1.0546 1.0629
垃圾箱= -2.5:.5:7.5;h =酒吧(垃圾箱,histc (x,垃圾箱)/(长度(x) * 5),“histc”);h.FaceColor =[。9。9。9);xgrid = linspace(1.1 *分钟(x), 1.1 *马克斯(x), 200);pdfgrid = pdf_normmixture (xgrid paramEsts (1) paramEsts (2), paramEsts (3), paramEsts (4), paramEsts (5));持有在图(的Xgrid,pdfgrid,“- - -”) 抓住从xlabel(“x”)ylabel(“概率密度”)
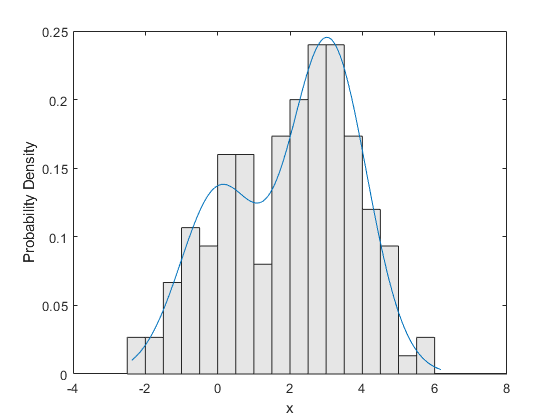
使用嵌套函数:一个普通例子不等精密工业
大中型企业来估计参数。X = [0.25 -1.24 1.38 1.39 -1.43 2.79 3.52 0.92 1.44 1.26];M = [8 2 1 3 8 4 2 5 2 4];
W = 1 ./ m
w =1×100.1250 0.5000 1.0000 0.3333 0.1250 0.2500 0.5000 0.2000 0.5000 0.2500
C .* exp(-0.5 .* z.^2),
大中型企业需要对PDF取对数,来计算对数可能性。因此,我们将创建一个直接计算日志PDF的函数。wgtnormfit.m.该函数包含数据初始化、加权正常模型中用于日志PDF的嵌套函数和对大中型企业函数来适应模型。因为必须是正的,我们必须指定参数的下界。调用大中型企业返回mu和sigma在单个向量中的最大似然估计。类型wgtnormfit.m
加权正态分布的拟合示例。% Copyright 1984-2012 The MathWorks, Inc. x = [0.25 -1.24 1.38 1.39 2.79 3.52 0.92 1.44 1.26]';M = [8 2 1 3 8 4 2 5 2 4]';函数= logpdf_wn(x,mu,sigma) v = sigma。^ 2。/ m;呆呆的= - (xμ)。^2 ./ (2.*v) - 5.*log(2.*pi.*v);结束paramEsts =大中型企业(x, logpdf, @logpdf_wn,‘开始’,(意思是(x)性病(x)],“低”,[负0]);结束
wgtnormfit.m,我们通过大中型企业嵌套函数的句柄logpdf_wn,使用'logpdf'参数。这个嵌套函数指的是在计算加权对数PDF时的观察计数m。因为向量m定义在它的父函数中,logpdf_wn可以访问它,而且不需要担心将m作为显式输入参数传入。wgtnormfit.m用途。开始= [平均(x)中,STD(x)]的
开始=1×21.0280 1.5490
paramEsts = wgtnormfit
paramEsts =1×20.6244 - 2.8823
使用参数转换:普通示例(续)
wgtnormfit2.m.与第一次匹配一样,该文件包含数据初始化、加权正常模型中用于日志PDF的嵌套函数以及对大中型企业函数来适应模型。因为西格玛可以是任何正值,日志(SIGMA)是无界的,我们不再需要指定下或上界。此外,呼叫大中型企业在这种情况下返回的参数估计和区间估计两者。类型wgtnormfit2.m
加权正态分布(log(sigma)参数化)的拟合示例。% Copyright 1984-2012 The MathWorks, Inc. x = [0.25 -1.24 1.38 1.39 2.79 3.52 0.92 1.44 1.26]';M = [8 2 1 3 8 4 2 5 2 4]';函数logpdf_wn2(x,mu,logsigma) v = exp(logsigma)。^ 2。/ m;呆呆的= - (xμ)。^2 ./ (2.*v) - 5.*log(2.*pi.*v);end [paramEsts,paramCIs] = mle(x, 'logpdf',@logpdf_wn2, 'start',[mean(x),log(std(x))]));结束
wgtnormfit2.m使用相同的起点,转换为新的参数化,即样本标准差的对数。开始= [(x),日志(std (x)))
开始=1×21.0280 - 0.4376
[paramEsts, paramCIs] = wgtnormfit2
paramEsts =1×20.6244 - 1.0586
paramCIs =2×2-0.2802 0.6203 1.5290 1.4969
muHat = paramEsts(1)
muHat = 0.6244
sigmaHat = exp (paramEsts (2))
sigmaHat = 2.8823
muCI = paramCIs (: 1)
muCI =2×1-0.2802 1.5290
sigmaCI = exp (paramCIs (:, 2))
sigmaCI =2×11.8596 - 4.4677

