广义帕累托分布

广义帕累托（GP）是右偏态分布，其形状参数，k和比例参数，西格玛参数化。k被也被称为“尾指数”参数，可以是正，零或负的。

x = linspace (0, 1000);情节(x, gppdf (x,。4, 1),“- - -”x, x, gppdf (0, 1),“- - -”,x, gppdf (x 2 1),“- - -”);包含(“x /σ”);ylabel (的概率密度);传奇({“k < 0”“k = 0”数k> 0'});

注意，对于k < 0, GP在-(1/k)的上限以上的概率为零。对于k >= 0, GP没有上限。此外，GP通常与第三个阈值参数一起使用，阈值参数将下限从0移开。我们不需要这种一般性。

在GP分布是两个指数分布（K = 0）和Pareto分布（K> 0）的概括。在GP包括在一个较大的家庭这两个分布，使得形状的连续范围是可能的。

模拟超过数数据

该GP分布能够建设性地超标来定义。的概率分布，其右尾部脱落到零开始，如正常的，我们可以独立地从该分布采样的随机值。如果我们确定的阈值，扔掉所有低于阈值的值，减去门槛关闭未抛出，结果被称为超标值的。超标的分布近似为GP。类似地，我们可以设置在一个分配的左尾部的阈值，而忽略高于阈值的所有值。该阈值必须在原分布的尾部远远不够出去近似是合理的。

原始分布决定了最终的GP分布的形状参数k。以多项式形式出现的分布，如学生的t，可以得到正的形状参数。尾部呈指数递减的分布，如正态分布，对应于零形参数。具有有限尾部的分布，如，对应于负形状参数。

对于GP分布真实世界的应用包括模拟股市收益的极端和建模特大洪水。在这个例子中，我们将使用模拟数据，有5个自由度的从学生的t分布产生。我们将采取从t分布2000点的观测最大的5％，再减去掉95％分位数得到超标。

rng (3“旋风”);x = trnd (2000 1);q =分位数(x, .95);y = x(x>q) - q;n =元素个数(y)

n = 100

分布拟合的最大似然

GP分布定义为0 < sigma， -Inf < k < Inf，但当k < -1/2时，对极大似然估计结果的解释是有问题的。幸运的是，这些情况对应于拟合来自beta或三角形分布的尾部，因此在这里不会出现问题。

paramEsts = gpfit (y);阿拉伯茶= paramEsts (1)尾部指数参数sigmaHat = paramEsts (2)%尺度参数

kHat = 0.0987, sigmaHat = 0.7156

正如预期的那样，由于使用一个t分布产生的模拟数据，k的估计是正的。

目测配合

为了直观地评估适合度有多好，我们将绘制一个缩放的尾部数据直方图，用我们估计的GP的密度函数覆盖。直方图被缩放，使得条形图的高度乘以宽度和为1。

垃圾箱= 0:.25:7;h =酒吧(垃圾箱,histc (y,垃圾箱)/ ((y) * .25长度),'histc');h.FaceColor = [0.9 0.9 0.9]。YGRID = linspace（0,1.1 *最大（Y），100）;线（YGRID，gppdf（YGRID，卡塔叶，sigmaHat））;XLIM（[0,6]）;包含(“超过数”);ylabel (的概率密度);

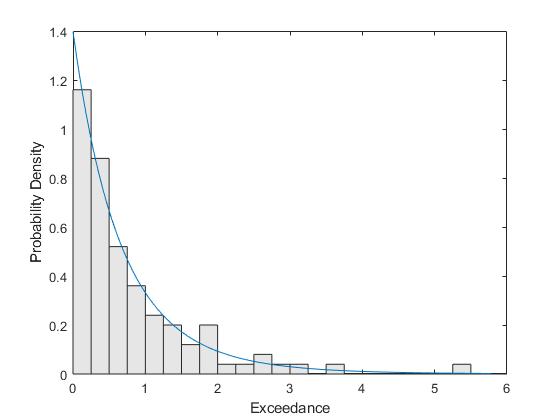
我们使用了一个相当小的箱子宽度，所以在直方图中有很多噪音。即便如此，拟合的密度仍然遵循数据的形状，因此GP模型似乎是一个不错的选择。

我们还可以将经验性CDF与拟合CDF进行比较。

[F,彝族]= ecdf (y);情节(咦,gpcdf(咦,阿拉伯茶,sigmaHat),“- - -”);保持在;楼梯(咦,F,“r”);保持离;传说（“合身广义Pareto CDF”,“经验提供”,'位置','东南');

计算标准误差参数估计值

为了量化估计的精度，我们将使用由最大似然估计器的渐近协方差矩阵计算出的标准误差。这个函数gplike计算，作为它的第二个输出，一个数值近似值的协方差矩阵。或者，我们可以打电话gpfit有两个输出参数，它将返回参数的置信区间。

[nll,acov] = gplike(paramEsts, y);stdErr =√诊断接头(acov))

标准错误= 0.1158 0.1093

这些标准的错误指示估计k的相对精度比相当低一点的西格玛 - 其标准误差是估计自身的顺序。外形参数往往很难估计。重要的是要记住，这些标准误差的计算假设GP模型是正确是很重要的，而且我们有渐近逼近协方差矩阵来保持足够的数据。

检验渐近正态性假设

标准误差的解释通常包括这样的假设:如果同一拟合可以对来自同一来源的数据重复多次，则参数的最大似然估计值将近似服从正态分布。例如，置信区间通常基于这个假设。

然而，这个正常的近似值可能是，也可能不是一个好的近似值。为了评估在这个例子中它有多好，我们可以使用一个引导模拟。我们将通过重新采样数据来生成1000个复制数据集，为每个数据拟合一个GP分布，并保存所有复制估计值。

@gpfit replEsts = bootstrp(1000年,y);

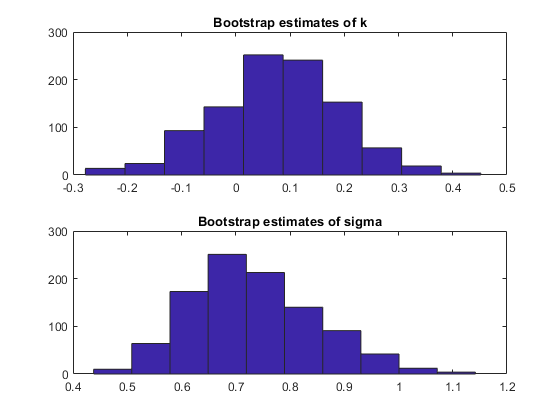
由于在参数估计量的抽样分布粗略的检查，我们可以看一下引导重复的直方图。

次要情节(2,1,1);嘘(replEsts (: 1));标题(“引导估计的k”);副区（2,1,2）;HIST（replEsts（：，2））;标题("西格玛的引导估计");

使用参数转换

k的bootstrap估计值的直方图只有一点不对称，而sigma估计值的直方图则明显向右偏。解决这种偏态的一个常用方法是在对数尺度上估计参数及其标准误差，在对数尺度上采用正态近似可能更合理。与直方图相比，Q-Q图是一种更好的评估正态性的方法，因为非正态性表现为不近似沿直线的点。我们来检查一下，看看对的对数变换是否合适。

次要情节(1、2、1);qqplot (replEsts (: 1));标题(“引导估计的k”);副区（1,2,2）;qqplot（日志（replEsts（：，2）））;标题(“引导估计日志(sigma)”);

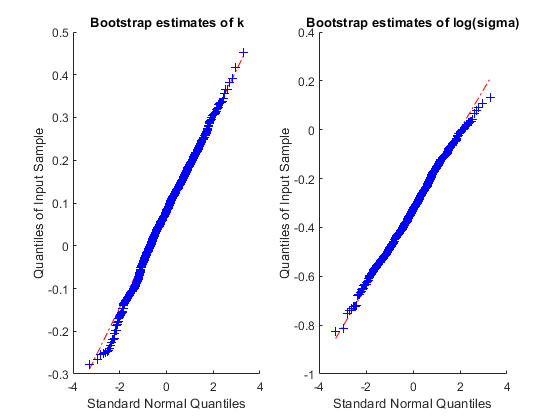
k和log(西格玛)的引导估计看起来接近正常。在未记录的范围内，对sigma的估计值进行Q-Q图，将证实我们在直方图中已经看到的偏态。因此，在正态性假设下，先计算一个log()的置信区间，然后取幂将其转换回原来的置信区间，这样更合理。

实际上，这就是这个函数gpfit做幕后。

[paramEsts, paramCI] = gpfit (y);

kHat kCI = paramCI(:，1)

kHat = 0.0987 kCI = -0.1283 0.3258

sigmaHat sigmaCI = paramCI(:，2)

sigmaHat = 0.7156, sigmaCI = 0.5305, 0.9654

请注意，虽然k的95%置信区间关于最大似然估计是对称的，但sigma的置信区间则不是。因为它是通过变换对称CI得到的。