使用Copulas模拟依赖随机变量

打开脚本

当变量之间存在复杂的关系时，或者当单个变量来自不同的分布时，这个例子展示了如何使用copula从多元分布中生成数据。

Matlab®是运行包含随机输入或噪声的模拟的理想工具。统计和机器学习工具箱™提供了根据许多常见的单变量分布来创建随机数据序列的功能。该工具箱还包括一些功能，可以从多变量分布生成随机数据，例如多变量正常和多变量t。然而，没有内置的方法来为所有边际分布产生多变量分布，或者在各个变量来自不同分布的情况下。

最近，Copulas在仿真模型中变得流行。Copulas是描述变量之间依赖性的函数，并提供创建分布以模拟相关多变量数据的方法。使用Copula，数据分析师可以通过指定边际单变量分布来构造多变量分布，并选择特定的Copula以提供变量之间的相关结构。双变量分布以及更高尺寸的分布。在此示例中，我们讨论如何使用Copulas使用统计和机器学习工具箱在Matlab中生成依赖多元随机数据。

仿真输入之间的依赖关系

蒙特卡罗模拟的设计决策之一是随机输入的概率分布的选择。为每个单独的变量选择一个分布通常很简单，但是决定输入之间应该存在什么依赖关系可能就不那么简单了。理想情况下，模拟的输入数据应该反映被建模的实际量之间的依赖性。然而，在仿真中可能很少或没有任何依赖的信息，在这种情况下，最好是用不同的可能性进行实验，以确定模型的灵敏度。

然而，当它们的分布不是来自标准多元分布时，实际上很难产生具有依赖性的随机输入。此外，一些标准的多元分布只能建模非常有限的依赖类型。总是有可能使输入独立，虽然这是一个简单的选择，但它并不总是明智的，可能会导致错误的结论。

例如，金融风险的蒙特卡罗模拟可能有代表不同保险损失来源的随机输入。这些输入可能被建模为对数正态随机变量。一个合理的问题是，这两个输入之间的依赖性如何影响模拟的结果。事实上，从真实数据中可以知道，相同的随机条件会影响两个来源，而在模拟中忽略这一点可能会导致错误的结论。

仿真独立的Lognormal随机变量是微不足道的。最简单的方式是使用lognrnd函数。这里，我们用mvnrnd函数生成n对独立的正态随机变量，然后对它们取幂。注意，这里使用的协方差矩阵是对角线的，即Z的列之间的独立性。

n = 1000;Sigma = .5;sigmaind = sigma。^ 2。* [1 0;0 1]

SigmaInd = 0.2500 00 0.2500

ZInd = mvnrnd([0 0]， SigmaInd, n);XInd = exp (ZInd);情节(XInd (: 1) XInd (:, 2),'。'）;轴平等的;轴([0 5 0 5]);Xlabel（X1的）;ylabel（“X2”）;

依赖于双变量Lognormal R.v.也可以使用具有非零对角线术语的协方差矩阵来易于生成。

ρ= 7;sigmadep = sigma。^ 2。* [1 rho;rho 1]

SigmaDep = 0.2500 0.1750 0.1750 0.2500

zdep = mvnrnd（[0 0]，sigmadep，n）;xdep = exp（zdep）;

第二个散点图说明了这两个二元分布之间的差异。

plot（xdep（：，1），xdep（:,2），'。'）;轴平等的;轴([0 5 0 5]);Xlabel（X1的）;ylabel（“X2”）;

很明显，在第二个数据集中X1的大值更倾向于与X2的大值相关联，对于小值也类似。这种相关性是由相关参数确定的，rho，的基础二元正态。从模拟中得到的结论很可能取决于X1和X2的生成是否具有相关性。

在这种情况下，二元对数正态分布是一个简单的解决方案，当然很容易推广到更高的维度和边缘分布的情况不同的对数正态。其他多元分布也存在，例如多元t分布和Dirichlet分布分别用来模拟相依t和beta随机变量。但是简单多元分布的列表并不长，它们只适用于边线都在同一家族中的情况(甚至完全相同的分布)。在许多情况下，这可能是一个真正的限制。

一种构建依赖性双变量分布的更通用方法

虽然上面创建二元对数正态的构造很简单，但它可以说明一种更普遍适用的方法。首先，我们从二元正态分布中生成成对的值。这两个变量之间存在统计依赖关系，每个变量都有一个正态边际分布。接下来，对每个变量分别应用一个变换(指数函数)，将边际分布转换为对数正态分布。变换后的变量仍然具有统计相关性。

如果可以找到合适的变换，可以推广该方法以创建与其他边缘分布的相关的双变量随机向量。事实上，确实存在构建这种转化的一般方法，尽管不像只是指数一样简单。

根据定义，对一个标准正态随机变量应用正态CDF(这里用PHI表示)得到的r.v在区间[0,1]上是均匀的。如果Z是标准正态分布，那么CDF (U) = (Z

Pr {u <= u0} = pr {phi（z）<= u0} = pr {z <= phi ^（ -  1）（u0）} = u0，

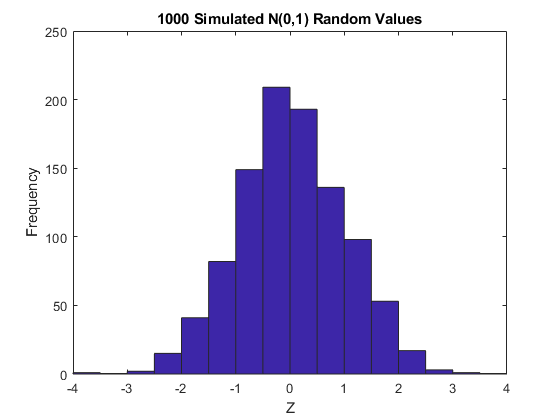
这是一个U(0,1) r.v的CDF。一些模拟的正态和转换值的直方图证明了这一事实。

n = 1000;z = normrnd（0,1，n，1）;HIST（Z，-3.75：.5：3.75）;XLIM（[ -  4 4]）;标题('1000模拟n（0,1）随机值'）;Xlabel（'z'）;ylabel（“频率”）;

u = normcdf（z）;hist（u，.05：.1：.95）;标题('1000模拟N（0,1）值转换为U（0,1）'）;Xlabel（“U”）;ylabel（“频率”）;

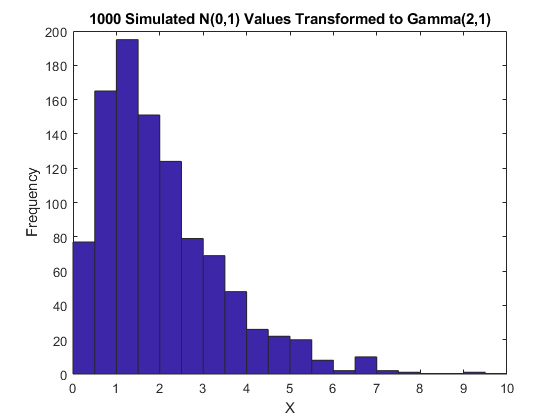
现在，从单变量随机数的理论借用，将任何分发F的反向CDF应用于U（0,1）随机变量的R.V。其分发正好是F.这被称为反演方法。证明基本上与前案件的上述证明相反。另一直方图说明了对伽马分布的转换。

x = gaminv（U，2,1）;hist（x，.25：.5：9.75）;标题('1000模拟N(0,1)值转换为Gamma(2,1)'）;Xlabel（'X'）;ylabel（“频率”）;

这两步变换可以应用于标准双变量正常的每个变量，创建依赖的R.v.具有任意边际分布。因为转换分别在每个组件上工作，所以两个结果为R.V.不需要具有相同的边际分布。转型定义为

z = [z1 z2]〜n（[0 0]，[1 rho; rho 1]）U = [phi（z1）phi（z2）] x = [g1（u1）g2（u2）]

其中G1和G2是两个可能不同的分布的逆CDF。例如，我们可以从与T（5）和伽马（2,1）边缘的双相抗体分布产生随机向量。

n = 1000;ρ= 7;Z = mvnrnd([0 0]， [1 rho;ρ1],n);U = normcdf (Z);X = [gaminv(U(:，1)，2,1) tinv(U(:，2)，5)];

该曲线与散点图具有直方图，以显示边缘分布和依赖。

[n1, ctr1] =嘘(X (: 1), 20);[n2, ctr2] =嘘(X (:, 2), 20);次要情节(2,2,2);情节(X (: 1) X (:, 2),'。'）;轴（[012-8 8]）;甘氨胆酸h1 =;标题(“1000模拟相关的t和伽马值”）;Xlabel（'x1〜伽玛（2,1）'）;ylabel（“X2 ~ t(5)”）;次要情节(2、2、4);酒吧(ctr1 n1 1);轴([0 12 -max(n1)*1.1 0]);轴('离开'）;甘氨胆酸h2 =;次要情节(2 2 1);barh (ctr2 n2 1);轴([-max(n2)*1.1 0 -8 8]);轴('离开'）;H3 = GCA;H1.Position = [0.35 0.35 0.55 0.55];H2.Position = [.35 .1 .55 .15];h3.Position = [.1 .35 .15 .55];Colormap（[.8 1]）;

等级相关系数

在这个结构中X1和X2之间的相关性由相关参数rho决定，rho是基础的二元正态分布。然而,它是不是，x1和x2的线性相关性是rho。例如，在原始的Lognormal案例中，有一个相关的表单：

cor（x1，x2）=（exp（rho. * sigma。^ 2） -  1）./（exp（sigma。^ 2） -  1）

除非rho正好一，否则这严格少于rho。然而，在更通用的情况下，例如上面的伽马/吨施工，X1和X2之间的线性相关性难以或不可能在ROO方面表达，但是仿真可以用来表明发生相同的效果。

这是因为线性相关系数表示线性r.v之间的依赖。当非线性变换应用于这些r。v。’s时，不保持线性相关。相反，一个等级相关系数，如Kendall's tau或Spearman's rho，是更合适的。

粗略地说，这些等级相关性衡量了一个r.v.的大或小值与另一个r.v.的大或小值的关联程度。然而，与线性相关系数不同的是，它们仅通过排名来衡量相关性。因此，在任何单调变换下都保持了秩相关性。特别地，刚才描述的变换方法保留了秩相关性。因此，知道二元正态Z的秩相关性，就决定了最终变换后的r.v的秩相关性。’s x。虽然rho仍然需要参数化潜在的二元正态，但Kendall’s tau或Spearman’s rho在描述r.v之间的依赖性时更有用。，因为它们对边际分布的选择是不变的。

结果表明，对于二元正态分布，在Kendall's tau或Spearman's rho和线性相关系数rho之间有一个简单的1-1映射:

等于(2/)*arcsin或= sin(/2) rho_s = (6/)*arcsin(/2)或= 2*sin(rho_s* /6)

次要情节(1 1 1);rho = -1：.01：1;tau = 2. * asin（rho）./ pi;rho_s = 6. * asin（rho./2）./ pi;情节（rho，tau，' - ', rho_sρ' - '，[-1 1]，[ -  1 1]，'k：'）;轴（[ -  1 1 -1 1]）;Xlabel（的ρ）;ylabel（等级相关系数的）;传奇(肯德尔”年代τ那斯皮尔曼”年代rho_s那“位置”那“西北”）;

因此，通过为Z1和Z2之间的线性相关选择正确的rho参数值，很容易创建X1和X2之间的期望的秩相关，而不考虑它们的边际分布。

注意，对于多元正态分布，Spearman的秩相关几乎等同于线性相关。然而，一旦我们转换到最终的随机变量，这就不成立了。

Copulas.

上述构造的第一步定义了所谓的谱，具体地是高斯谱系的内容。一双变量仅仅是两个随机变量的概率分布，每个边际分布都是均匀的。这两个变量可以是完全独立的，确定介绍（例如，U2 = U1），或者之间的任何内容。双抗体高斯共克拉斯的系列由rho = [1 rho参数化。Rho 1]，线性相关矩阵。U1和U2接近线性依赖作为RHO方法+/- 1，并将完全独立作为ROO接近零。

不同rho能级下的一些模拟随机值的散点图说明了高斯耦合器的不同可能范围:

n = 500;Z = mvnrnd([0 0]， [1 8;1。8),n);U = normcdf (Z, 0,1);次要情节(2 2 1);情节(U (: 1), U (:, 2),'。'）;标题('rho = 0.8'）;Xlabel（‘U1’）;ylabel（“U2”）;Z = mvnrnd([0 0]， [1 1;1。1,n);U = normcdf (Z, 0,1);次要情节(2,2,2);情节(U (: 1), U (:, 2),'。'）;标题(ρ= 0.1的）;Xlabel（‘U1’）;ylabel（“U2”）;z = mvnrnd（[0 0]，[1 -.1; -.1 1]，n）;U = normcdf (Z, 0,1);次要情节(2、2、3);情节(U (: 1), U (:, 2),'。'）;标题('rho = -0.1'）;Xlabel（‘U1’）;ylabel（“U2”）;Z = mvnrnd([0 0]， [1 -.8];-．8 1], n);U = normcdf (Z, 0,1);次要情节(2、2、4);情节(U (: 1), U (:, 2),'。'）;标题('rho = -0.8'）;Xlabel（‘U1’）;ylabel（“U2”）;

U1和U2之间的依赖性与X1 = G（U1）和X2 = G（U2）的边际分布完全分开。可以给出x1和x2任何边际分布，仍然有相同的秩相关。这是耦合函数的主要吸引力之一——它们允许对依赖关系和边际分布进行单独说明。

t连系动词

可以通过从二抗体T分布开始和使用相应的T CDF转换来构建不同的Copulas系列。双变量T分布用RHO，线性相关矩阵和NU参数化，自由度。因此，例如，我们可以分别基于多变量T，谈论T（1）或T（5）族，分别具有一个和五个自由度。

各级ROO的一些模拟随机值的散点图说明了T（1）Copulas的不同可能性的范围：

n = 500;ν= 1;t = mvtrnd（[1 .8; .8 1]，nu，n）;U = tcdf (T,ν);次要情节(2 2 1);情节(U (: 1), U (:, 2),'。'）;标题('rho = 0.8'）;Xlabel（‘U1’）;ylabel（“U2”）;T = mvtrnd([1;1 1]， nu, n);U = tcdf (T,ν);次要情节(2,2,2);情节(U (: 1), U (:, 2),'。'）;标题(ρ= 0.1的）;Xlabel（‘U1’）;ylabel（“U2”）;T = mvtrnd([1 - 1;-．1 1]， nu, n);U = tcdf (T,ν);次要情节(2、2、3);情节(U (: 1), U (:, 2),'。'）;标题('rho = -0.1'）;Xlabel（‘U1’）;ylabel（“U2”）;t = mvtrnd（[1 -.8; -.8 1]，nu，n）;U = tcdf (T,ν);次要情节(2、2、4);情节(U (: 1), U (:, 2),'。'）;标题('rho = -0.8'）;Xlabel（‘U1’）;ylabel（“U2”）;

A t连接函数对U1和U2有均匀的边际分布，就像高斯连接函数一样。t连接函数中各分量之间的秩相关tau或rho_s对于高斯函数也是相同的。然而，正如这些图所示，t(1)连接函数与高斯连接函数有很大的不同，即使它们的分量具有相同的秩相关。不同之处在于它们的依赖结构。毫不奇怪，当自由度参数变大时，一个t(nu)联系函数趋向于相应的高斯联系函数。

与高斯谱一样，任何边缘分布都可以施加在T Copula上。例如，使用具有1度自由度的T copula，我们可以再次从双方与Gab（2,1）和T（5）边缘的双变量分布产生随机向量：

次要情节(1 1 1);n = 1000;ρ= 7;ν= 1;T = mvtrnd([1;1]， n);U = tcdf (T,ν);X = [gaminv(U(:，1)，2,1) tinv(U(:，2)，5)];[n1, ctr1] =嘘(X (: 1), 20);[n2, ctr2] =嘘(X (:, 2), 20); subplot(2,2,2); plot(X(:,1),X(:,2),'。'）;轴([0 15 -10 10]);甘氨胆酸h1 =;标题(“1000模拟相关的t和伽马值”）;Xlabel（'x1〜伽玛（2,1）'）;ylabel（“X2 ~ t(5)”）;次要情节(2、2、4);酒吧(ctr1 n1 1);轴([0 15 -max(n1)*1.1 0]);轴('离开'）;甘氨胆酸h2 =;次要情节(2 2 1);barh (ctr2 n2 1);Axis ([-max(n2)*1.1 0 -10 10]);轴('离开'）;H3 = GCA;H1.Position = [0.35 0.35 0.55 0.55];H2.Position = [.35 .1 .55 .15];h3.Position = [.1 .35 .15 .55];Colormap（[.8 1]）;

与之前构建的基于高斯copula的二元Gamma/t分布相比，这里构建的基于t(1) copula的分布具有相同的边际分布和变量之间相同的秩相关，但依赖结构非常不同。这说明了多元分布不是由它们的边际分布或它们的相关性唯一定义的事实。在应用程序中选择特定的copula可以基于实际观测数据，也可以使用不同的copula作为确定模拟结果对输入分布的敏感性的一种方法。

高阶连系动词

高斯和T Copulas被称为椭圆形共型。它很容易通过椭圆的共芯片概括到更高数量的维度。例如，我们可以使用GAMAIS opula与伽马（2,1），BETA（2,2）和T（5）边缘的速降分布模拟数据。

次要情节(1 1 1);n = 1000;rho = [1 .4 .2;.4 1 -.8;.2 -.8 1];z = mvnrnd（[0 0 0]，rho，n）;U = normcdf (Z, 0,1);x = [gaminv（u（：，1），2,1）贝纳韦（U（：，2），2,2）Tinv（U（：，3），5）];plot3（x（：，1），x（:,2），x（:,3），'。'）;网格在;视图([15]-55年);Xlabel（‘U1’）;ylabel（“U2”）;zlabel (U3的）;

请注意，线性相关参数rho和(例如Kendall’s)之间的关系适用于这里使用的相关矩阵rho中的每一项。我们可以验证数据的样本秩相关近似等于理论值。

tauTheoretical = 2π* asin(ρ)。/

TautheOrative = 1.0000 0.2620 0.1282 0.2620 1.0000 -0.5903 0.1282 -0.5903 1.0000

tauSample = corr (X,'类型'那“假象”）

Tausample = 1.0000 0.2655 0.1060 0.2655 1.0000 -0.6076 0.1060 -0.6076 1.0000

Copulas和经验边缘分布

为了使用copula模拟依赖的多元数据，我们已经看到我们需要指定

1) copula族(和任何形状参数)，2)变量之间的秩相关，3)每个变量的边际分布

假设我们有两套库存回报数据，我们希望使用蒙特卡罗模拟，其中输入与我们的数据相同的分布。

负载储存者脑袋=大小(股票,1);次要情节(2,1,1);嘘(股票(:1)10);Xlabel（X1的）;ylabel（“频率”）;次要情节(2,1,2);嘘(股票(:,2),10);Xlabel（“X2”）;ylabel（“频率”）;

(这两个数据向量有相同的长度，但这不是关键。)

我们可以分别拟合一个参数模型到每个数据集，并使用这些估计作为我们的边际分布。然而，参数化模型可能不够灵活。相反，我们可以使用边际分布的经验模型。我们只需要一种计算逆CDF的方法。

这些数据集的经验反向CDF只是一个阶段函数，有一个步骤1 / nobs，2 / nobs，...... 1.步高度只是排序数据。

INVCDF1 = SORT（库存（：，1））;n1 =长度（库存（：，1））;INVCDF2 = SORT（库存（：，2））;n2 =长度（库存（：，2））;次要情节(1 1 1);楼梯（（1：nobs）/ nobs，Invcdf1，'B'）;抓住在;楼梯(invCDF2(1:脑袋)/脑袋,'r'）;抓住离开;传奇(X1的那“X2”）;Xlabel（'累积概率'）;ylabel（'X'）;

为了模拟，我们可能想用不同的copula和相关性进行实验。在这里，我们将使用一个具有相当大的负相关参数的双变量t(5) copula。

n = 1000;ρ=。8;ν= 5;T = mvtrnd([1;1]， n);U = tcdf (T,ν);X = [invCDF1(装天花板(n1 * U (: 1))) invCDF2(装天花板(n2 * U (:, 2))));[n1, ctr1] =嘘(X (: 1), 10);[n2, ctr2] =嘘(X (:, 2), 10);次要情节(2,2,2); plot(X(:,1),X(:,2),'。'）;轴([-3.5 3.5 -3.5 3.5]);甘氨胆酸h1 =;标题('1000模拟依赖价值'）;Xlabel（X1的）;ylabel（“X2”）;次要情节(2、2、4);酒吧(ctr1 n1 1);轴（[ -  3.5 3.5 -max（n1）* 1.1 0]）;轴('离开'）;甘氨胆酸h2 =;次要情节(2 2 1);barh (ctr2 n2 1);轴([-max(n2)*1.1 0 -3.5 3.5]);轴('离开'）;H3 = GCA;H1.Position = [0.35 0.35 0.55 0.55];H2.Position = [.35 .1 .55 .15];h3.Position = [.1 .35 .15 .55];Colormap（[.8 1]）;

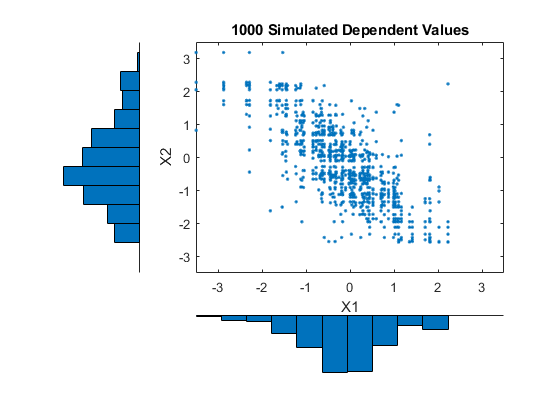
模拟数据的边缘直方图与原始数据的边缘直方图紧密匹配，并且随着我们模拟更多的数值，将变得相同。请注意，值从原始数据中绘制，并且由于每个数据集中只有100个观察，因此模拟数据有点“离散”。克服这一点的一种方法是添加少量随机变化，可能通常分布到最终的模拟值。这相当于使用经验逆CDF的平滑版本。