旅行推销员问题:具体问题具体分析
这个例子展示了如何使用二进制整数规划来解决经典的旅行商问题。这个问题涉及找到最短的封闭之旅(路径)通过一组停止(城市)。在这种情况下,有200停止,但你可以很容易地改变nStops变量大小不同的问题。你会解决最初的问题,看到解决方案subtours。这意味着最优解发现没有给一个连续路径通过所有的点,而是有几个断开连接的循环。然后您将使用一个迭代过程确定subtours,添加约束和运行优化直到subtours消除。
solver-based的方法这个问题,看到的旅行推销员问题:Solver-Based。
问题公式化
制定的旅行推销员问题整数线性规划如下:
生成所有可能的旅行,这意味着所有的成对的停止。
计算每个旅行的距离。
成本函数最小化旅行距离之和为每个访问之旅。
决策变量是二进制,与每一个旅行,其中每个1表示存在于旅游的行程,和每个0代表一个旅行而不是旅游。
确保旅游包括每一停止,包括线性约束,每一站到底两次。这意味着一个到来,一个离开停止。
生成停止
生成随机停止在一个原油的多边形表示美国大陆
负载(“usborder.mat”,“x”,“y”,“xx”,“yy”);rng (3“旋风”)%就停在缅因州、佛罗里达州,是可再生的nStops = 200;%你可以用任意数量,但问题规模的N ^ 2stopsLon = 0 (nStops, 1);%分配nStops x坐标stopsLat = stopsLon;%分配坐标n = 1;而(n < = nStops) xp =兰特* 1.5;yp =兰德;如果inpolygon (xp, yp, x, y)%在边界测试stopsLon (n) = xp;stopsLat (n) = yp;n = n + 1;结束结束
计算点之间的距离
因为有200停止,19900年有19900次,这意味着二进制变量(变量= 200号选择2)。
生成所有的旅行,这意味着所有成对的停止。
idx = nchoosek (1: nStops, 2);
计算所有旅行的距离,假设地球是平为了使用毕达哥拉斯规则。
dist =函数(stopsLat (idx (: 1))——stopsLat (idx (:, 2)),…stopsLon (idx (: 1))——stopsLon (idx (:, 2)));lendist =长度(经销);
这个定义的经销向量,参观的长度
dist”*旅行
在哪里旅行是二进制向量代表的旅行解决方案。这是旅行的距离,你尽量减少。
创建图表,画地图
代表图的问题。创建一个图形,停止节点和边旅行。
图G = (idx (: 1), idx (:, 2));
用图表显示停止阴谋。阴谋没有图形边缘节点。
图hGraph =情节(G,“XData”stopsLon,“YData”stopsLat,“线型”,“没有”,“NodeLabel”,{});持有在%画出边界之外情节(x, y,的r -)举行从
创建变量和问题
创建一个二进制优化变量优化问题代表了潜在的旅行。
tsp = optimproblem;旅行= optimvar (“旅行”lendist 1“类型”,“整数”,下界的0,“UpperBound”1);
包括问题的目标函数。
tsp。目标=距离' *旅行;
约束
创建线性约束,每一站有两个相关的旅行,因为必须有一个去每一站和离开每一站的旅程。
用图表示识别所有旅行开始或结束停止通过寻找所有边缘连接,停止。对于每个停止,创建的和旅行的约束,阻止= 2。
constr2trips = optimconstr (nStops, 1);为停止= 1:nStops whichIdxs = outedges (G,停止);%确定旅行与停止constr2trips(停止)=总和(trips (whichIdxs)) = = 2;结束tsp.Constraints。constr2trips = constr2trips;
解决最初的问题
问题是可以解决的。抑制迭代输出,关闭默认显示。
选择= optimoptions (“intlinprog”,“显示”,“关闭”);tspsol =解决(茶匙,“选项”选择)
tspsol =结构体字段:旅行(19900×1双):
可视化解决方案
创建一个新的旅行作为边缘图的解决方案。为此,在解决方案中一些值不是整数,并转换生成的值逻辑。
tspsol。旅行= logical(round(tspsol.trips)); Gsol = graph(idxs(tspsol.trips,1),idxs(tspsol.trips,2),[],numnodes(G));% Gsol =图(idx (tspsol.trips, 1), idx (tspsol.trips 2));%在大多数情况下同样适用
覆盖现有的新图形情节和突出的边缘。
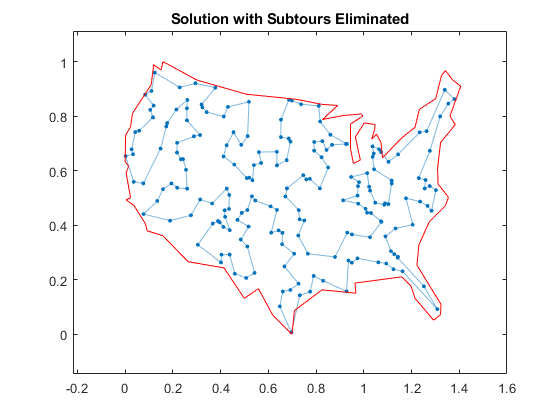
持有在突出(hGraph Gsol,“线型”,“- - -”)标题(“解决方案与Subtours”)

在地图上可以看到,解决方案有几个subtours。到目前为止没有指定的约束阻止这些subtours发生。为了防止任何可能的subtour情况发生,你将需要一个令人难以置信的大量的不等式约束。
Subtour约束
因为你不能添加的所有subtour约束,采用迭代的方法。检测subtours在当前的解决方案,然后添加不等式约束,以防止这些特定的subtours发生。通过这样做,你会找到一个合适的旅游在一些迭代。
消除subtours不等式约束。这是如何工作的一个例子是如果你有5分subtour,然后是五行连接这些点来创建subtour。消除这种subtour通过实现一个不等式约束说必须小于或等于四行这5分之间。
更多,找到所有这些5分之间的界限,限制的解决方案没有超过四行。这是一个正确的约束,因为如果5或更多的行中存在一个解决方案,解决方案会有subtour(图表 节点和 边缘总是包含一个周期)。
检测subtours通过确定连接组件Gsol与边缘图,建立在当前的解决方案。conncomp返回一个向量的数量每条边所属subtour。
tourIdxs = conncomp (Gsol);numtours = max (tourIdxs);%的subtours数量流(“# subtours: % d \ n”,numtours);
# subtours: 27
包括线性不等式约束来消除subtours,反复调用解算器,直到只剩下一个subtour。
% subtours添加约束指数k = 1;而numtours > 1直到只有一个subtour %重复%添加subtour约束为2 = 1:numtours inSubTour = (tourIdxs = = 2);在当前subtour %边缘一个= (inSubTour (idx), 2);%完全图指数subtour两端constrname =“subtourconstr”+ num2str (k);tsp.Constraints。(constrname) = (trips (a))和< = (nnz (inSubTour) - 1);k = k + 1;结束%再次优化[tspsol, fval exitflag、输出]=解决(茶匙,“选项”、选择);tspsol。旅行= logical(round(tspsol.trips)); Gsol = graph(idxs(tspsol.trips,1),idxs(tspsol.trips,2),[],numnodes(G));% Gsol =图(idx (tspsol.trips, 1), idx (tspsol.trips 2));%在大多数情况下同样适用%绘制新的解决方案hGraph。线型=“没有”;%删除之前的突出显示的路径突出(hGraph Gsol,“线型”,“- - -”)drawnow%多少subtours呢?tourIdxs = conncomp (Gsol);numtours = max (tourIdxs);%的subtours数量流(“# subtours: % d \ n”numtours)结束
# subtours: 20 # subtours: 7 # subtours: 9 # subtours: 9 # subtours: 3 # subtours: 2 # subtours: 7 # subtours: 2 # subtours: 1
标题(“解决方案与Subtours消除”);持有从
解决方案质量
解决方案是一个可行的旅游,因为它是一个闭环。但这是最小成本之旅吗?发现的一个方法是检查输出结构。
disp (output.absolutegap)
0
渺小的绝对差距意味着解决方案是最优或接近最优的总长度。
