古典摆:一些Algorithm-Related问题

这个例子显示了如何估计算法的选择可能会影响非线性灰色框模型估计的结果。我们使用非线性摆系统产生的数据,这是示意图如图1所示。我们展示特别是微分方程解算器的选择如何影响结果。

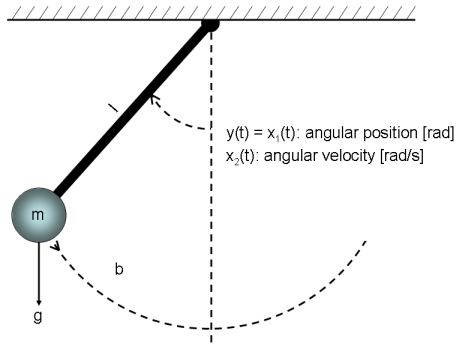
图1:古典摆的示意图。

输出数据

我们开始建模旅游通过加载输出数据(时间序列数据)。数据包含一个输出,y,摆角位置的(rad)。角为零当钟摆向下,并增加逆时针。有1001(模拟)的样本数据和样品时间是0.1秒。摆是影响重力不变,但没有其他外生力量影响摆的运动。调查这种情况下,我们创建一个IDDATA对象:

负载(fullfile (matlabroot“工具箱”,“识别”,“iddemos”,“数据”,“pendulumdata”));z = iddata (y, [], 0.1,“名字”,“摆”);z。OutputName =“摆的位置”;z。OutputUnit =rad的;z。Tstart = 0;z。TimeUnit =“年代”;

摆角位置的(输出)情节窗口所示。

图(“名字”,(z.Name:输出数据的]);情节(z);

图2:摆角位置(输出)。

摆造型

下一步是指定一个钟摆系统模型结构。它的动力学研究在许多书籍和文章,是众所周知的事情。如果我们选择x1 (t)的角位置(rad)和x2 (t)的角速度(rad / s)摆,然后而是简单的建立一个整数的结构如下:

d / dt x1 (t) = x2 (t) d / dt x2 (t) = - (g / l) * sin (x1 (t))——(b / l ^ 2)) (m * * x2 (t)

y (t) = x1 (t)

有参数(或常数)

g -引力常数(m / s ^ 2) l -摆杆长度的[m] b -粘性摩擦系数(Nms / rad) m -鲍勃的摆的质量(公斤)

我们这个信息输入pendulum_m MATLAB文件。米,内容如下:

函数(dx, y) = pendulum_m (t, x, u, g, l, b, m,变长度输入宗量)% pendulum_m摆系统。

%输出方程。y = x (1);%角位置。

%状态方程。dx = [x (2);…%角位置。- (g / l) * sin (x (1)) - b / (m * l ^ 2) * x (2)……%角速度。];

下一步是创建一个通用IDNLGREY对象用于描述摆。我们也进入信息的单位名称和输入,输出和参数。由于物理现实所有模型参数必须是积极的,这是由所有参数的“最小值”属性设置为最小的可辨认的正值MATLAB®, eps (0)。

文件名=“pendulum_m”;%文件描述模型结构。订单= [1 0 2];%模型[纽约νnx]命令。参数= (9.81;1;0.2;1);%初始参数。InitialStates = [1;0);%初始初始状态。t = 0;%的时间连续系统。nlgr = idnlgrey(文件名、秩序、参数InitialStates Ts);nlgr。OutputName =“摆的位置”;nlgr。OutputUnit =rad的;nlgr。TimeUnit =“年代”;nlgr = setinit (nlgr,“名字”,{“摆的位置”“摆速度”});nlgr = setinit (nlgr,“单位”,{rad的“rad / s”});nlgr = setpar (nlgr,“名字”,{“引力常数”“长度”…的摩擦系数“质量”});nlgr = setpar (nlgr,“单位”,{“米/秒^ 2”“米”“Nms / rad”“公斤”});nlgr = setpar (nlgr,“最低”,{eps(0)每股收益(0)每股收益(0)每股收益(0)});%所有参数> 0。

三个初始摆模型的性能

之前试图估计任何参数我们模拟系统的猜解参数值。我们做三个可用的解决者,欧拉向前与固定步长(ode1),龙格-库塔23自适应步长(ode23),并与自适应步长龙格-库塔45(数值)。当使用获得的输出这三个解决情节窗口所示。

% a模型计算一阶欧拉向前ODE求解器进行求解。nlgref = nlgr;nlgref.SimulationOptions。解算器=“ode1”;%欧拉向前。nlgref.SimulationOptions。FixedStep = z.Ts * 0.1;%步长。% b模型计算自适应龙格-库塔23 ODE求解器进行求解。nlgrrk23 = nlgr;nlgrrk23.SimulationOptions。解算器=“ode23”;%龙格-库塔23。% c模型计算自适应龙格-库塔45 ODE求解器进行求解。nlgrrk45 = nlgr;nlgrrk45.SimulationOptions。解算器=“数值”;%龙格-库塔45。比较(z, nlgref, nlgrrk23 nlgrrk45 1,…compareOptions (“InitialCondition”,“模型”));

图3:比较真实的输出和模拟输出的三个初始摆模型。

可以看到,结果向前欧拉方法(细网格使用比默认情况下)获得的结果有很大区别与龙格-库塔解决者。在这种情况下,事实证明,欧拉向前解算器产生一个相当好的结果(合适的模型),而输出与龙格-库塔获得解决有点有限。然而,这有点欺骗,以后也将变得显而易见,因为b的初始值,粘滞摩擦系数,是现实的两倍。

参数估计

引力常数g,杆的长度,l,鲍勃的质量,m,可以很容易地测量或来自一个表没有评估。然而,这通常不是这样的摩擦系数,通常必须估计。因此我们修复前三个参数g = 9.81 l = 1,和m = 1,而只考虑b作为一个自由参数:

nlgref = setpar (nlgref,“固定”{真的真的假的真});nlgrrk23 = setpar (nlgrrk23,“固定”{真的真的假的真});nlgrrk45 = setpar (nlgrrk45,“固定”{真的真的假的真});

接下来,我们使用三个微分方程解决估计b。我们开始向前欧拉模型结构。

选择= nlgreyestOptions (“显示”,“上”);微软目前=时钟;nlgref = nlgreyest (z, nlgref,选择);%进行参数估计。微软目前=结束(时钟,微软);

然后我们继续解决模型基于龙格-库塔23 (ode23)。

trk23 =时钟;nlgrrk23 = nlgreyest (z, nlgrrk23,选择);%进行参数估计。trk23 =结束(时钟、trk23);

我们终于用龙格-库塔45解算器(数值)。

trk45 =时钟;nlgrrk45 = nlgreyest (z, nlgrrk45,选择);%进行参数估计。trk45 =结束(时钟、trk45);

三个估计摆模型的性能

当使用这三种动力学结果总结如下。b的真正价值是0.1,这是获得与数值。0.1 ode23返回一个值非常接近,而ode1返回值相当距离0.1。

disp (“估计时间估计b值”);流(' ode1: % 3.1 f % 1.3 f \ n”微软,nlgref.Parameters (3) value);流(' ode23: % 3.1 f % 1.3 f \ n”、trk23 nlgrrk23.Parameters (3) value);流('数值:% 3.1 f % 1.3 f \ n”、trk45 nlgrrk45.Parameters (3) value);

然而,这并不意味着模拟输出不同,从实际的输出,因为错误产生的不同解决微分方程通常占估计过程。这是一个事实,随时可以看到通过模拟三个估计摆模型。

比较(z, nlgref, nlgrrk23 nlgrrk45 1,…compareOptions (“InitialCondition”,“模型”));

图4:比较真实的输出和模拟输出的三个估计摆模型。

如预期这个数字,最后预测误差(消防工程)准则值这些模型也相当接近对方:

消防工程(nlgref nlgrrk23 nlgrrk45);

在此基础上,我们得出这样的结论:这三个模型能够捕捉摆动力学,但基于欧拉向前模型反映了底层物理很差。增加其“物理学”性能的唯一方法就是减少步长求解程序,但是这也意味着解决方案时间显著增加。我们的实验表明,龙格-库塔45 non-stiff问题的解决是最好的解算器,当考虑到精度和运算速度。

结论

龙格-库塔45(数值)解算器经常返回高质量结果相对较快,因此被选为默认IDNLGREY微分方程解算器。“帮助idnlgrey打字。SimulationOptions”提供了一些更详细的解决者和打字”帮助nlgreyestOptions”提供了各种估计选项的详细信息,可用于IDNLGREY建模。

额外的信息

更多信息的识别与系统辨识工具箱™访问动态系统系统辨识工具箱产品信息页面。