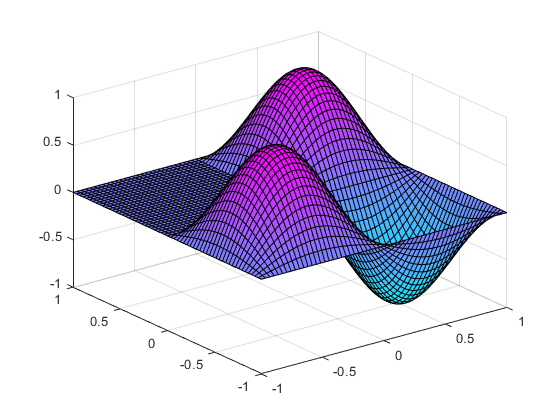
这个例子展示了如何解决L形区域上拉普拉斯算子的特征值问题。
考虑一个固定在边界上的膜 的一个地区 在平面上。它的位移 是由特征值问题描述的 哪里 是拉普拉斯算子和吗 是标量参数。边界条件为 总的来说 .
拉普拉斯算子是自伴和负定的,也就是说,只有实负特征值 存在。有一个极大的(负的)离散特征值,对应的特征函数 被称为基态.在这个例子中, 为L形区域,与该区域相关的基态为L形膜,即MATLAB®徽标。
特征值问题的最简单方法是近似拉普拉斯方程
通过有限差分近似(a模板)在有距离的点组成的正方形网格上hx在
方向和距离沪元在
方向。在这个例子中,是近似的
有一笔钱S_h围绕中点的九个常规栅格点的
.未知量就是权重
.
符号u(x,y)每股收益a11a10a1_1a01a00a0_1a_11a_10a_1_1符号hx沪元积极的S_h = a_11 * u(x - Eps*hx,y + Eps*hy) +...a01*u(x,y+Eps*hy)+...a11*u(x+Eps*hx,y+Eps*hy)+...a_10*u(x-Eps*hx,y)+...a00*u(x,y)+...(b + b) b + b (c + b) b...a_1_1*u(x-Eps*hx,y-Eps*hy)+...a0_1*u(x,y-每股收益*hy)+...a1_1*u(x+Eps*hx,y-Eps*hy);
使用符号参数每股收益按的幂对这个表达式的展开进行排序hx和沪元.知道了权重,你可以通过设置来近似拉普拉斯矩阵每股收益= 1.
t =泰勒(S_h, Eps,“秩序”, 7);
使用多项式系数函数来提取幂相同的项的系数每股收益.每个系数都是包含的幂的表达式hx,沪元的导数u关于
和
.自S_h代表
,其他导数的系数u必须为零。通过替换的所有导数提取系数u,除了
和
, 0。取代
和
1。这将泰勒展开式简化为您想要计算的系数,并引出以下六个线性方程。
C=公式(系数(t,Eps,“所有”))(7)u(x,y,y,y),1)==0;eq11=sub(C(6),[dif(u,x,x,x,(u,y,y)及[1,0,(1,0)0,[1,0,(0)eq0=0;eq0=0;EQQ1=0;EQ1=0;EQ1=0=0;eq11=0=0(C(C(C(6),[C(C(6),[C(6),[dif(u,x,(u,x,(u,x,x,x,x,x,x,x,x,x,x,x,x,(u,x,(u,x,x,(u,x,x,x,x,x,x),u,u,x),u,y,y)(u,(u,y,y,u,y)及y)],,,[u,y,(u,y,(u,(u,y,x,(u,y,y 1,0])==0;eq23=subs(C(5),[diff(u,x,x),diff(u,x,y),diff(u,y,y)],[0,0,1])==1;
因为里面有九个未知的重量S_h,通过要求所有的三阶导数u都是0。
eq31 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [1, 0, 0, 0) = = 0;eq32 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [0 1 0,0]) = = 0;eq33 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [0, 0, 1, 0]) = = 0;eq34 =潜艇(C (4), (diff (u, x, x, x), diff (u, x, x, y), diff (u, x, y, y) diff (u, y, y, y)], [0, 0, 0, 1]) = = 0;
解得到的10个方程,得到9个未知权重。使用ReturnConditions求包含任意参数的所有解。万博 尤文图斯
(a11 a10, a1_1、a01 a00、a0_1, a_11, a_10, a_1_1,参数、条件)=...解决([eq0, eq11、eq12 eq21, eq22, eq23, eq31, eq32, eq33, eq34),...(a11 a10, a1_1、a01 a00、a0_1, a_11, a_10, a_1_1),...“返回条件”,真正的);扩大([a_11 a01, a11;...a_10,a00,a01;...a1_1,a0_1,a_1_1])
ans =
参数
参数=
使用潜艇函数将权重替换为其计算值。
C=简化(subs(C));
表情C (7),C (6),C (4)包含的0阶,1阶和3阶导数u消失。
[C(7)、C(6)、C (4))
ans =
表达式C (5)是拉普拉斯的吗u.
C (5)
ans =
因此,根据上面计算的权重值,模板S_h近似拉普拉斯阶hx ^ 2,hy ^ 2对于任意参数的任意值z,前提是z是有秩序的吗O(1/hx^2,1/hy^2).
虽然解决方案包含一个自由参数z,该表达式C (3)包含的四阶导数u不能通过选择合适的z.另一个选择是把它变成拉普拉斯算子的平方的倍数。
符号d拉普拉斯= @(u)拉普拉斯(u,[x,y])扩大(d *拉普拉斯(拉普拉斯(u)))
ans(x,y)=
取不同的导数u在C (3),并使它们的系数与相应的项相等。
潜艇(C (3), [diff (u, x, x, x, x), diff (u, x, x, y, y), diff (u, y, y, y, y)], [1, 0, 0)) = = d
ans =
潜艇(C (3), [diff (u, x, x, x, x), diff (u, x, x, y, y), diff (u, y, y, y, y)], [0, 1,0]) = = 2 * d
ans =
subs(C(3),[diff(u,x,x,x,x),diff(u,x,x,y,y),diff(u,y,y,y)],[0,0,1])==d
ans =
因此,你可以选择d=hx^2/12=hy^2/12和z = 2 * d / (hx hy ^ ^ 2 * 2),这意味着hx =沪元和z = 1 / (6 * hx *衔接).因此,模板S_h在正方形网格上近似一个改进的拉普拉斯算子Hx = hy = h.
符号hhx = h;hy = h;d = h ^ 2/12;
取代hx和沪元通过h.
C=subs(C);
取代z的价值,1/(6*h^2).因为z在MATLAB®工作空间中不存在,您只能将其作为存储在参数数组中。
C=subs(C,参数,1/(6*h^2));
验证公式(1)。
简化(C(3)-d*Laplace(Laplace(u)))
ans(x,y)=
现在考虑三阶项hx,沪元.
简化(C (2))
ans =
由于在模板的扩展中不存在这样的术语,该术语 在(1)是事实上的秩序 .考虑模具的四阶项。
因子(简化(C (1)))
ans =
检查这些项是否可以和拉普拉斯算子的另一次幂联系起来。然而,与
拉普拉斯(拉普拉斯(拉普拉斯(u)))
ans(x,y)=
显示顺序的表达式 无法识别为拉普拉斯算子三次幂的某些倍数,因为系数无法匹配。
对于具有距离的正方形网格h在相邻的网格点和上面选择的权重之间,你得到:
将此展开式用于特征值问题的数值方法 .加上的倍数 到特征值方程。
这个等式的左边可以很好地用模板来近似 .因此,使用(2),一个数值特征值 模板的效果令人满意 一定是特征值的近似值 的拉普拉斯算子
对于给定 ,解决 为了获得拉普拉斯特征值的更好近似值,请注意,在求解二次方程时 平方根的正确符号由以下要求给出: 为 .
考虑一个l型区域 由三个单元正方形组成。
定义区域角落的坐标值。
xmin=-1;xmax=1;ymin=-1;ymax=1;
考虑一个由奇数组成的正方形网格Nx = 2 * nx-1网格点的x方向与奇数纽约= 2 * ny-1网格点的y方向。
nx = 6;Nx = 2 * nx-1;hx = (xmax-xmin) / (Nx-1);纽约= 6;纽约= 2 * ny-1;hy = (ymax-ymin) / (Ny-1);
创建一个纽约-借-Nx符号矩阵
.它的条目u(i,j)表示值u(xmin+(j-1)*hx,ymin+(i-1)*hy)解决方案u(x,y)关于特征值问题
.
u=sym(“u”(纽约Nx]);
的边界 对应以下指数:
左边界对应于(i = 1:Ny, j = 1).
下边界对应于(i = 1, j = 1:Nx).
右边界对应于(i = 1:ny, j = Nx)和(i = ny: ny, j = nx).
上界对应于(i = Ny, j =1:nx)和(i = ny, j = nx: nx).
u (: 1) = 0;%左边界u (1) = 0;%下边界u(1:纽约,Nx) = 0;%右边界,上部u(纽约:纽约,nx) = 0;%右边界,下部u(Ny,1:nx)=0;%左上边界u(ny,nx:nx)=0;%右上边界
该地区与
和
不属于
.设置相应的矩阵项(i=ny+1:ny,j=nx+1:nx)归零。它们不再扮演进一步的角色,将被忽略。
u(ny + 1: ny,nx + 1: nx) = 0;
问题的未知量为以下矩阵项:
u
u=
该区域的内部点
对应于指数
包含未知值
这个问题。将这些未知数收集到一个向量中var.
[I,J]=find(u~=0);vars=u(u~=0);
将符号表达式(由本例第一部分中派生的模板给出)与每个索引(即每个未知数)关联。
n =长度(var);陆=符号(0 (n, 1));为k=1:ni=i(k);j=j(k);Lu(k)=1/6*u(i+1,j-1)+2/3*u(i+1,j)+1/6*u(i+1,j+1)...+ 2/3*u(I,j+1) - 10/3*u(I,j) + 2/3*u(I,j+1)...+1 /6*u(i-1,j-1) + 2/3*u(i-1,j) +1 /6*u(i-1,j+1);结束陆=陆/ hx ^ 2;
因为这个表达式在未知元素中是线性的u(储存于var),可以将其视为作用于向量的矩阵var.
S_h=雅可比(Lu,vars);
你可以请客S_h作为拉普拉斯算子的矩阵近似。计算它的特征向量和特征值。
[V D] = eig (vpa (S_h));
三个最大特征值由D的第一对角元素给出。
【D(1,1)、D (2, 2), D (3,3)]
ans =
因为对于这种近似,您使用了一个具有少量点的网格,所以只有特征值的前导数字是正确的。
l形区域上拉普拉斯算子的第三大特征值 是清楚的。拉普拉斯算子的准确本征函数就是这个函数 与(精确的)特征值有关 .实际上,使用上面的方程(3),你可以得到拉普拉斯特征值的一个更好的近似 从模板特征值 :
mu=D(3,3)
亩=
λ=2*亩/(平方米(1+亩*hx^2/3)+1)
兰姆达=
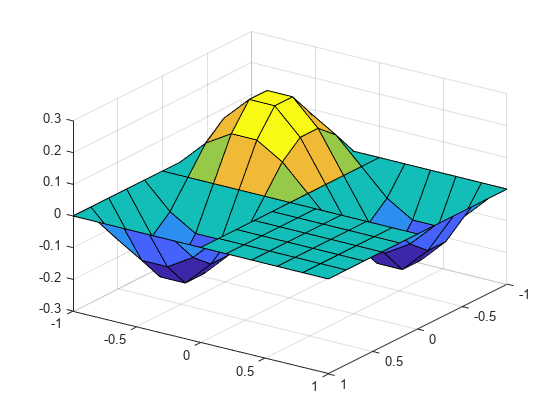
绘制与第三个最高特征值相关联的特征函数。
v=v(:,3);为k=1:nu(I(k),J(k))=v(k);结束u =双(u);冲浪(xmin: hx: xmax ymin::为什么ymax, u ');视图(125年,30);

当您使用符号矩阵时,不建议大幅增加网格点的数量,因为符号计算比MATLAB双精度矩阵的数值计算要慢得多。这个例子的这一部分演示了如何使用稀疏双精度算法来细化数值网格。l型区域
设置的方式和以前一样。不要用符号未知数来表示内部点,而是初始化网格值u一个一个地定义
通过将边界点和外部点的值设为零。不是为每个内部点定义一个符号表达式并计算模具作为雅可比矩阵,而是直接将模具矩阵设置为一个稀疏矩阵。
xmin=-1;xmax=1;ymin=-1;ymax=1;nx = 30;Nx = 2 * nx-1;hx = (xmax-xmin) / (Nx-1);纽约= 30;纽约= 2 * ny-1;hy = (ymax-ymin) / (Ny-1);u =(纽约、Nx);u (: 1) = 0;%左边界u(1:纽约,Nx) = 0;%右边界,上部u(纽约:纽约,nx) = 0;%右边界,下部u (1) = 0;%下边界u(Ny,1:nx)=0;%左上边界u(ny,nx:nx)=0;%右上边界u(ny + 1: ny,nx + 1: nx) = 0;[I,J] = find(u ~= 0);n =长度(我);S_h =稀疏(n, n);为k=1:n i = i (k)j = (k);S_h(k,I== I +1 & J== J +1)= 1/6;S_h(k,I== I +1 & J== J)= 2/3;S_h(k,I== I +1 & J== J -1)= 1/6;S_h(k,I== I & J== J +1)= 2/3;S_h(k,I== I & J== J)=-10/3;S_h(k,I== I & J== J -1)= 2/3;S_h(k,I== I -1 & J== J +1)= 1/6;S_h(k,I== I -1 & J== J)= 2/3; S_h(k,I==i-1 & J==j-1)= 1/6;结束S_h=S_h./hx^2;
在这里,S_h为(稀疏)模板矩阵。使用eigs它处理稀疏矩阵来计算三个最大的特征值。
[V D] = eigs (S_h 3“洛杉矶”);
三个最大特征值是D的第一对角元素。
【D(1,1)、D (2, 2), D (3,3)]
ans =1×3-9.6493 -15.1742 -19.7006
D(3,3)近似精确的特征值
.利用上面的方程(3),导出拉普拉斯特征值的更精确的近似
从模板特征值
.
mu=D(3,3)
μ= -19.7006
λ=2*亩/(平方米(1+亩*hx^2/3)+1)
λ=-19.7393
绘制与第三个最高特征值相关联的特征函数。
v=v(:,3);为k=1:nu(I(k),J(k))=v(k);结束冲浪(xmin: hx: xmax ymin::为什么ymax, u ');视图(125年,30);
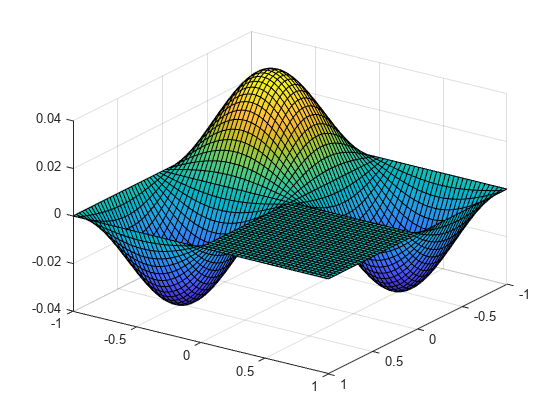
注意MATLAB膜函数通过不同的方法计算拉普拉斯算子的特征函数。
膜(3,nx-1,8,8);