セクタ境界とセクタンデックスにいて

円錐セクタ

最も単純な形式では，円錐セクタ，は2本のラ，ン<年代pan class="inlineequation"> $y ＝一个 u$ と<年代pan class="inlineequation"> $y ＝ b u$ で区切られた2次元領域です。

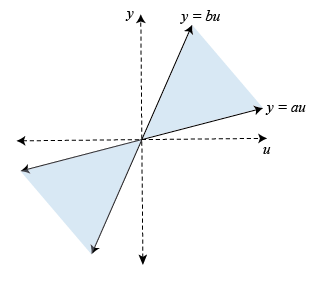
影付き領域は不等式<年代pan class="inlineequation"> $（ y - 一个 u ）（ y - b u ） < 0$ で特徴付けられます。より一般的には，このようなセクターは次のようにパラメーター化できます。

${（ \begin{array}{c} y \\ u \end{array} ）}^{T} 问（ \begin{array}{c} y \\ u \end{array} ） < 0 ，$

ここで，<年代pan class="inlineequation"> $问$ は2行2列の対称不定行列(<年代pan class="inlineequation"> $问$ には正の固有値が1と負の固有値が1含まれる)です。<年代pan class="inlineequation"> $问$ は<年代pan class="emphasis">“セクタ，行列”と呼ばれます。この概念は高次元にも一般化されます。N次元空間の場合、円錐セクターは次の集合になります。

$年代＝｛ z \in R^{N} ： z^{T} 问 z < 0 ｝，$

ここでも<年代pan class="inlineequation"> $问$ は対称不定行列です。

セクタ，境界

セクタ，境界はシステムの動作に対する制約です。ゲ@ @ンの制約と受動性の制約はセクター境界の特殊ケースにあたります。すべての非ゼロ入力軌跡が<年代pan class="inlineequation"> $u （ t ）$ の場合，線形システム<年代pan class="inlineequation"> $H （年代）$ の出力軌跡<年代pan class="inlineequation"> $z （ t ）＝（ H u ）（ t ）$ は次を満たします。

$\int_{0}^{T} z^{T} （ t ）问 z （ t ） d t < 0 ， \forall T > 0 ，$

この場合，<年代pan class="inlineequation"> $H$ の出力軌跡は行列<年代pan class="inlineequation"> $问$ をも円錐セクタ内に配置されます。異なる行列<年代pan class="inlineequation"> $问$ を選択すると，システムの応答に異なる条件が課されます。たとえば，軌跡<年代pan class="inlineequation"> $y （ t ）＝（ G u ）（ t ）$ および次の値を考えます。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array} ）．$

これらの値は次のセクタ，境界に相当します。

$\int_{0}^{T} {（ \begin{array}{c} y （ t ） \\ u （ t ） \end{array} ）}^{T} （ \begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array} ）（ \begin{array}{c} y （ t ） \\ u （ t ） \end{array} ） d t < 0 ， \forall T > 0 ．$

このセクタ，境界は次に示す<年代pan class="inlineequation"> $G （年代）$ の受動性条件と等価です。

$\int_{0}^{T} y^{T} （ t ） u （ t ） d t > 0 ， \forall T > 0 ．$

まり，受動性は，次で定義されるシステムにおける特別なセクタ，境界です。

$H ＝（ \begin{array}{c} G \\ 我 \end{array} ）．$

周波数領域の条件

時間領域の条件はすべての<年代pan class="inlineequation"> $T > 0$ で成立しなければならないため,等価な周波数領域の境界を導出するには若干の注意が必要であり,常に可能とは限りません。以下の

$问＝ W_{1}^{T} W_{1} - W_{2}^{T} W_{2}$

を，不定行列<年代pan class="inlineequation"> $问$ をその正の部分と負の部分に(任意に)分解したものであるとします。<年代pan class="inlineequation"> $W_{2}^{T} H （年代）$ が正方で最小位相(不安定な零点をもたない)の場合，時間領域の条件

$\int_{0}^{T} （ H u ）（ t ）^{T} 问（ H u ）（ t ） d t < 0 ， \forall T > 0$

は，次の周波数領域の条件と同等です。

$H （ j ω ）^{H} 问 H （ j ω ） < 0 \forall ω \in R ．$

このため，実周波数のセクタ，の不等式を確認するだけで十分です。<年代pan class="inlineequation"> $问$ の分解を使用すると，これは次とも等価になります。

${‖ （ W_{1}^{T} H ）（ W_{2}^{T} H ）^{- 1} ‖}_{\infty} < 1 ．$

$W_{2}^{T} H$ が正方になるのは<年代pan class="inlineequation"> $问$ の負の固有値の数が<年代pan class="inlineequation"> $H （年代）$ の入力チャネルと同数の場合であることに注意してください。この条件が満たされない場合，実周波数を確認するだけでは(一般的に)不十分です。また，<年代pan class="inlineequation"> $W_{2}^{T} H （年代）$ が正方の場合，これは，セクタ，境界が成立するためには最小位相でなければなりません。

この周波数領域の特性は<一个href="//www.tianjin-qmedu.com/jp/help/control/ref/lti.sectorplot.html" data-docid="control_ref#bu6l1bj-1" class="a">sectorplotのベ，スとなります。具体的には，sectorplotは<年代pan class="inlineequation"> $（ W_{1}^{T} H （ j ω ））（ W_{2}^{T} H （ j ω ））^{- 1}$ の特異値を周波数の関数としてプロットします。セクタ，境界は,最大特異値が 1 未満に留まる場合にのみ満たされます。さらに、プロットには、セクター境界が満たされるのか違反されるのかや、満たされる度合いまたは違反される度合いといった周波数帯域に関する有用な情報が含まれます。

たとえば，特定のセクタにいて2出力2入力システムのセクタプロットを調べます。

rng (4<年代pan style="color:#A020F0">“旋风”）;H = rss(3,4,2);Q = [-5.12 2.16 -2.04 2.17 2.16 -1.22 -0.28 -1.11 -2.04 -0.28 -3.35 0.00 2.17 -1.11 0.00 - 0.18);sectorplot (H, Q)

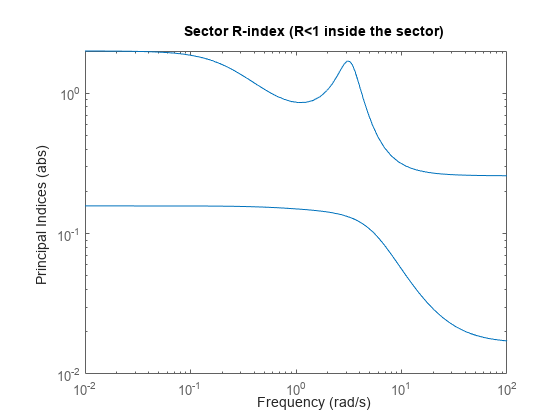
图中包含一个轴对象。axis对象包含2个line类型的对象。这个对象表示H。

プロットは，<年代pan class="inlineequation"> $（ W_{1}^{T} H （ j ω ））（ W_{2}^{T} H （ j ω ））^{- 1}$ の最大特異値が,およそ0.5 rad / sより下の帯域と3 rad / sあたりの狭い帯域内で1を上回っていることを示します。したがって，Hは问で表されるセクタ，境界を満たしていません。

相対セクタンデックス

相対受動性▪▪ンデックスの概念を任意のセクタ▪▪に拡張できます。<年代pan class="inlineequation"> $H （年代）$ をltiシステムとし，

$问＝ W_{1}^{T} W_{1} - W_{2}^{T} W_{2} ， W_{1}^{T} W_{2} ＝ 0$

は,<年代pan class="inlineequation"> $问$ の正の部分と負の部分への直交分解とします。これは，<年代pan class="inlineequation"> $问$ の舒尔分解で簡単に取得できます。<年代pan class="emphasis">“相対セクタンデックス”<年代pan class="inlineequation"> $R$ (r▪▪ンデックス)は、すべての出力軌跡<年代pan class="inlineequation"> $z （ t ）＝（ H u ）（ t ）$ にいて次を満たす最小の<年代pan class="inlineequation"> $r > 0$ として定義されます。

$\int_{0}^{T} z^{T} （ t ）（ W_{1}^{T} W_{1} - r^{2} W_{2}^{T} W_{2} ） z （ t ） d t < 0 ， \forall T > 0 ．$

$r$ を増やすと<年代pan class="inlineequation"> $W_{1}^{T} W_{1} - r^{2} W_{2}^{T} W_{2}$ がさらに負になるため，不等式は通常<年代pan class="inlineequation"> $r$ が十分に大きい場合に満たされます。ただし，決して満たされないこともあり，その場合，r escンデックスは<年代pan class="inlineequation"> $R ＝ + \infty$ です。元のセクタ，境界が満たされるのは<年代pan class="inlineequation"> $R \leq 1$ の場合のみであることは明らかです。

R▪▪▪▪ンデックスの幾何学的解釈を理解するには、行列<年代pan class="inlineequation"> $问（ r ）＝ W_{1}^{T} W_{1} - r^{2} W_{2}^{T} W_{2}$ をも円錐ファミリを考えます。2次元では，円錐の傾斜角度<年代pan class="inlineequation"> $θ$ は<年代pan class="inlineequation"> $r$ と次のような関係にあります。

$棕褐色（ θ ）＝ r \frac{‖ W_{2} ‖}{‖ W_{1} ‖}$

(以下の図を参照)。より一般的には，<年代pan class="inlineequation"> $棕褐色（ θ ）$ は<年代pan class="inlineequation"> $R$ に比例します。したがって，行列<年代pan class="inlineequation"> $问$ をも円錐セクタが与えられた場合，rンデックス値<年代pan class="inlineequation"> $R < 1$ は,<年代pan class="inlineequation"> $H$ の出力軌跡の一部が円錐セクタ，を離れる前に<年代pan class="inlineequation"> $棕褐色（ θ ）$ を係数<年代pan class="inlineequation"> $R$ で縮小(円錐を細く)できることを意味します。同様に，値<年代pan class="inlineequation"> $R > 1$ は,<年代pan class="inlineequation"> $H$ の出力軌跡をすべて含めるには<年代pan class="inlineequation"> $棕褐色（ θ ）$ を係数<年代pan class="inlineequation"> $R$ で増大させ(円錐を広げ)なければならないことを意味します。これにより，明らかに，r escンデックスは<年代pan class="inlineequation"> $H$ の応答がどの程度特定の円錐セクタ，に収まるかを示す相対尺度になります。

この図では

$d_{1} \frac{| W_{1}^{T} z |}{‖ W_{1} ‖} ， d_{2} \frac{| W_{2}^{T} z |}{‖ W_{2} ‖} ， R ＝ \frac{| W_{1}^{T} z |}{| W_{2}^{T} z |} ，$

および

$棕褐色（ θ ）＝ \frac{d_{1}}{d_{2}} ＝ R \frac{‖ W_{2} ‖}{‖ W_{1} ‖} ．$

$W_{2}^{T} H （年代）$ が正方で最小位相の場合，r esc escンデックスは周波数領域で次を満たす最小の<年代pan class="inlineequation"> $r > 0$ として特徴付けることもできます。

$H （ j ω ）^{H} （ W_{1}^{T} W_{1} - r^{2} W_{2}^{T} W_{2} ） H （ j ω ） < 0 \forall ω \in R ．$

初等代数学ではこれは以下になります。

$R ＝ \underset{ω}{马克斯} ‖ （ W_{1}^{T} H （ j ω ））（ W_{2}^{T} H （ j ω ））^{- 1} ‖ ．$

言い換えれば，r恭顺器ンデックスは(安定した)伝達関数<年代pan class="inlineequation"> $Φ （年代）：＝（ W_{1}^{T} H （年代））（ W_{2}^{T} H （年代））^{- 1}$ のピクゲンであり，<年代pan class="inlineequation"> $Φ （ j w ）$ の特異値は各周波数の"主成分" r escンデックスと見なすことができます。これにより，r escンデックスと周波数のプロットが特異値のプロットのように見える理由もわかります(<一个href="//www.tianjin-qmedu.com/jp/help/control/ref/lti.sectorplot.html" data-docid="control_ref#bu6l1bj-1" class="a">sectorplotを参照)。相対セクタンの間には完全な相似があります。ただし，この相似は<年代pan class="inlineequation"> $W_{2}^{T} H （年代）$ が正方で最小位相の場合にのみ成立します。

方向セクタンデックス

同様に，方向受動性。行列<年代pan class="inlineequation"> $问$ をも<年代pan class="inlineequation"> $δ 问$ の場合，方向セクタ<年代pan class="inlineequation"> $z （ t ）＝（ H u ）（ t ）$ で次が満たされるような最大の<年代pan class="inlineequation"> $τ$ になります。

$\int_{0}^{T} z^{T} （ t ）（问 + τ δ 问） z （ t ） d t < 0 ， \forall T > 0 ．$

システム<年代pan class="inlineequation"> $G （年代）$ の方向受動性@ @ンデックスは次に相当します。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array} ）．$

方向セクタンデックスは，<年代pan class="inlineequation"> $H$ の出力軌跡の周囲にぴったり合わせるために，セクタ，を方向<年代pan class="inlineequation"> $δ 问$ にどれだけ変形させる必要があるかで測定されます。セクタ，境界は方向インデックスが正の場合にのみ満たされます。

共通のセクタ

セクタ，境界を指定する方法は多数あります。次に，よく使われる式を検討し，それに対応するシステム<年代pan class="inlineequation"> $H$ およびセクタ，行列<年代pan class="inlineequation"> $问$ を,getSectorIndexおよびsectorplotで使用される標準形式に対し指定します。

$\int_{0}^{T} （ H u ）（ t ）^{T} 问（ H u ）（ t ） d t < 0 ， \forall T > 0 ．$

簡単にするために，これらの説明では次の表記を使用します。

$‖ x ‖_{T} ＝ \int_{0}^{T} ‖ x （ t ） ‖^{2} d t ，$

また，<年代pan class="inlineequation"> $\forall T > 0$ の要件を省略します。

受動性

受動性は次で表されるセクタ，境界です。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} 0 & - 我 \\ - 我 & 0 \end{array} ）．$

ゲ@ @ンの制約

ゲ@ @ンの制約<年代pan class="inlineequation"> ${‖ G ‖}_{\infty} < γ$ は次で表されるセクタ，境界です。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} 我 & 0 \\ 0 & - γ^{2} 我 \end{array} ）．$

距離の割合

次の“内部”の制約を考えます。

$‖ y - c u ‖_{T} < r ‖ u ‖_{T}$

ここで，<年代pan class="inlineequation"> $c ， r$ はスカラ，で，<年代pan class="inlineequation"> $y （ t ）＝（ G u ）（ t ）$ です。これは次で表されるセクタ，境界です。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} 我 & - c 我 \\ - c 我 & （ c^{2} - r^{2} ）我 \end{array} ）．$

基礎となる円錐セクタ，は<年代pan class="inlineequation"> $y ＝ c u$ に対して対称です。同様に，“外部”の制約

$‖ y - c u ‖_{T} > r ‖ u ‖_{T}$

は次で表されるセクタ，境界です。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} - 我 & c 我 \\ c 我 & （ r^{2} - c^{2} ）我 \end{array} ）．$

二重不等式

静的な非線形性を扱う場合，次の形式の円錐セクタ，を検討するのが一般的です。

$一个 u^{2} < y u < b u^{2} ，$

ここで，<年代pan class="inlineequation"> $y ＝ ϕ （ u ）$ は非線形出力です。この関係自体はセクタ，境界ではありませんが，明らかに次を示します。

$一个 \int_{0}^{T} u （ t ）^{2} d t < \int_{0}^{T} y （ t ） u （ t ） d t < b \int_{0}^{T} u （ t ）^{2} d t$

これは，すべてのI/O軌跡に沿って，またすべての<年代pan class="inlineequation"> $T > 0$ にます。この条件は次で表されるセクタ，境界と同等になります。

$H （年代）＝（ \begin{array}{c} ϕ （．） \\ 1 \end{array} ），问＝（ \begin{array}{cc} 1 & - （一个 + b ） / 2 \\ - （一个 + b ） / 2 & 一个 b \end{array} ）．$

乗算形式

次の形式の一般化されたセクタ，境界

$\int_{0}^{T} （ y （ t ） - K_{1} u （ t ））^{T} （ y （ t ） - K_{2} u （ t ）） d t < 0$

は次に相当します。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝（ \begin{array}{cc} 2 我 & - （ K_{2} + K_{1}^{T} ） \\ - （ K_{1} + K_{2}^{T} ） & K_{1}^{T} K_{2} + K_{2}^{T} K_{1} \end{array} ）．$

前述のように，次の静的セクタ，境界

$（ y - K_{1} u ）^{T} （ y - K_{2} u ） < 0$

は上記の積分セクタ，境界を示します。

QSR散逸

次を満たす場合，システム<年代pan class="inlineequation"> $y ＝ G u$ はQSR散逸です。

$\int_{0}^{T} {（ \begin{array}{c} y （ t ） \\ u （ t ） \end{array} ）}^{T} （ \begin{array}{cc} 问 & 年代 \\ {年代}^{T} & R \end{array} ）（ \begin{array}{c} y （ t ） \\ u （ t ） \end{array} ） d t > 0 ， \forall T > 0 ．$

これは次で表されるセクタ，境界です。

$H （年代）＝（ \begin{array}{c} G （年代） \\ 我 \end{array} ），问＝ - （ \begin{array}{cc} 问 & 年代 \\ {年代}^{T} & R \end{array} ）．$

参照

[1]夏，M.， P. Gahinet, N. Abroug, C. Buhr, E. Laroche。稳定性分析与控制设计中的扇形边界国际鲁棒与非线性控制杂志第30期。18(2020年12月):7857-82。<一个href="https://doi.org/10.1002/rnc.5236" target="_blank">https://doi.org/10.1002/rnc.5236．

参考
getSectorIndex|<年代pan itemscope itemtype="//www.tianjin-qmedu.com/help/schema/MathWorksDocPage/SeeAlso" itemprop="seealso">sectorplot|<年代pan itemscope itemtype="//www.tianjin-qmedu.com/help/schema/MathWorksDocPage/SeeAlso" itemprop="seealso">getSectorCrossover

関連するトピック

受動性および受動性▪▪▪ンデックスに▪▪▪いて

例を開く

この例の変更されたバ，ジョンがあります.編集された方の例を開きますか?

いいえ，変更されたバ，ジョンを上書きします。<一个id="open-example-dialog-continue" class="btn btn_color_blue" data-dismiss="modal">はい

Matlabコマンド

次のmatlabコマンドに対応するリンクがクリックされました。

コマンドをmatlabコマンドウィンドウに入力して実行してください。Webブラウザ，はMATLABコマンドをサポ，トしていません。

选择网站

选择一个网站，在可用的地方获得翻译的内容，并查看当地的活动和优惠。根据您所在的位置，我们建议您选择:<年代trong class="recommended-country">．

瑞士(英语)

瑞士(德语)

瑞士(法语)

中国 (简体中文)

中国(英文)

您也可以从以下列表中选择一个网站:

如何获得最佳的网站性能

选择中国站点(中文或英文)以获得最佳站点性能。其他MathWorks国家站点没有针对您所在位置的访问进行优化。

美洲

 美国拉丁（西班牙语)

加拿大（英语)

美国（英语)

欧洲

 比利时（英语)

丹麦（英语)

德国（德语)

西班牙（西班牙语)

芬兰（英语)

法国（法语)

爱尔兰（英语)

意大利（意大利语)

卢森堡（英语)

荷兰（英语)

挪威（英语)

奥地利（德语)

葡萄牙（英语)

瑞典（英语)

瑞士

 多伊奇

 英语

 法语

 联合王国（英语)

亚太地区

 澳大利亚（英语)

印度（英语)

新西兰（英语)

中国

 简体中文

 英语

 日本(日本語)

한국(한국어)

联系当地办事处