振子の周期的揺れの動きのシミュレ，ションgydF4y2Ba

この例では符号数学工具箱™を使用して単純な振子の動きをモデル化する方法を示します。振子の運動方程式を導出し,その方程式を小角について解析的に解き,任意の角度について数値的に解きます。gydF4y2Ba

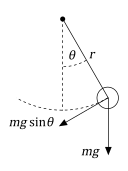
手順1:運動方程式の導出gydF4y2Ba

振子は，微分方程式に従う単純な機械的システムです。振子は，初期状態では垂直位置で停止しています。振子がある角度gydF4y2Ba $θgydF4y2Ba$ だけ動かされ放されると，重力によりその静止位置へ引っ張られます。その運動量により行き過ぎて角度gydF4y2Ba $-gydF4y2Ba θgydF4y2Ba$ に達し(摩擦力がない場合)，これを繰り返します。重力による振子の動きに伴う復元力はgydF4y2Ba $-gydF4y2Ba 米gydF4y2Ba ggydF4y2Ba 罪gydF4y2Ba θgydF4y2Ba$ です。したがって，ニュ，トンの第2法則に従って，質量と加速度の積はgydF4y2Ba $-gydF4y2Ba 米gydF4y2Ba ggydF4y2Ba 罪gydF4y2Ba θgydF4y2Ba$ に等しくなければなりません。gydF4y2Ba

信谊gydF4y2Ba米gydF4y2Ba一个gydF4y2BaggydF4y2Baθ(t)gydF4y2BaEqn = m*a == -m*g*sin(theta)gydF4y2Ba

eqn (t) =gydF4y2Ba
                   $一个gydF4y2Ba 米gydF4y2Ba ＝gydF4y2Ba -gydF4y2Ba ggydF4y2Ba 米gydF4y2Ba 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba$

長さがgydF4y2Ba $rgydF4y2Ba$ の振子では，振子の重りの加速度は角加速度にgydF4y2Ba $rgydF4y2Ba$ を乗じたものです。gydF4y2Ba

$一个gydF4y2Ba ＝gydF4y2Ba rgydF4y2Ba \frac{{dgydF4y2Ba}^{2gydF4y2Ba} θgydF4y2Ba}{dgydF4y2Ba {tgydF4y2Ba}^{2gydF4y2Ba}}$ ．gydF4y2Ba

潜艇gydF4y2BaをgydF4y2Ba $一个gydF4y2Ba$ の代わりに使用します。gydF4y2Ba

信谊gydF4y2BargydF4y2BaEqn = subs(Eqn,a,r*diff(theta,2))gydF4y2Ba

eqn (t) =gydF4y2Ba
                  
                    $米gydF4y2Ba rgydF4y2Ba \frac{{\partialgydF4y2Ba}^{2gydF4y2Ba}}{\partialgydF4y2Ba {tgydF4y2Ba}^{2gydF4y2Ba}} θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ＝gydF4y2Ba -gydF4y2Ba ggydF4y2Ba 米gydF4y2Ba 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba$

隔离gydF4y2Baを使用してgydF4y2BaeqngydF4y2Ba内の角加速度を分離します。gydF4y2Ba

Eqn = isolate(Eqn,diff(theta,2))gydF4y2Ba

eqn =gydF4y2Ba
                  
                    $\frac{{\partialgydF4y2Ba}^{2gydF4y2Ba}}{\partialgydF4y2Ba {tgydF4y2Ba}^{2gydF4y2Ba}} θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ＝gydF4y2Ba -gydF4y2Ba \frac{ggydF4y2Ba 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba}{rgydF4y2Ba}$

定数gydF4y2Ba $ggydF4y2Ba$ およびgydF4y2Ba $rgydF4y2Ba$ を"固有振動数"gydF4y2Baとしても知られる単一のパラメ，タ，にまとめます。gydF4y2Ba

${ωgydF4y2Ba}_{0gydF4y2Ba} ＝gydF4y2Ba \sqrt{\frac{ggydF4y2Ba}{rgydF4y2Ba}}$ 。gydF4y2Ba

信谊gydF4y2Baomega_0gydF4y2BaEqn = s(Eqn,g/r, 0^2)gydF4y2Ba

eqn =gydF4y2Ba
                  
                    $\frac{{\partialgydF4y2Ba}^{2gydF4y2Ba}}{\partialgydF4y2Ba {tgydF4y2Ba}^{2gydF4y2Ba}} θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ＝gydF4y2Ba -gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba}^{2gydF4y2Ba} 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba$

手順2:運動方程式の線形化gydF4y2Ba

この運動方程式は非線形であるため解析的な求解が困難です。角度が小さいと仮定して，gydF4y2Ba $罪gydF4y2Ba θgydF4y2Ba$ のテ▪▪ラ▪▪展開を使用して方程式を線形化します。gydF4y2Ba

信谊gydF4y2BaxgydF4y2Ba近似= taylor(sin(x) x，gydF4y2Ba“秩序”gydF4y2Ba2);近似= subs(近似，x， (t))gydF4y2Ba

约=gydF4y2Ba
                   $θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba$

運動方程式は線形方程式になります。gydF4y2Ba

eqnLinear = subs(eqn,sin((t))，近似)gydF4y2Ba

eqnLinear =gydF4y2Ba
                  
                    $\frac{{\partialgydF4y2Ba}^{2gydF4y2Ba}}{\partialgydF4y2Ba {tgydF4y2Ba}^{2gydF4y2Ba}} θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ＝gydF4y2Ba -gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba}^{2gydF4y2Ba} θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba$

手順3:運動方程式の解析的な求解gydF4y2Ba

方程式gydF4y2BaeqnLineargydF4y2BaをgydF4y2BadsolvegydF4y2Baを使用して解きます。初期条件を2番目の引数として指定します。gydF4y2Ba假设gydF4y2Baを使用してgydF4y2Ba ${ωgydF4y2Ba}_{0gydF4y2Ba}$ が実数であると仮定して，解を単純化します。gydF4y2Ba

信谊gydF4y2Batheta_0gydF4y2Batheta_t0gydF4y2BaTheta_t = diff(theta);Cond = [theta(0) == theta_0, theta_t(0) == theta_t0];假设(omega_0gydF4y2Ba“真实”的gydF4y2Ba) thetaSol(t) = dsolve(eqnLinear,cond)gydF4y2Ba

thetaSol (t) =gydF4y2Ba
                  
                    ${θgydF4y2Ba}_{0gydF4y2Ba} 因为gydF4y2Ba （gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba} tgydF4y2Ba ）gydF4y2Ba +gydF4y2Ba \frac{{θgydF4y2Ba}_{t0gydF4y2Ba} 罪gydF4y2Ba （gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba} tgydF4y2Ba ）gydF4y2Ba}{{ωgydF4y2Ba}_{0gydF4y2Ba}}$

手順 4:gydF4y2Ba ${ωgydF4y2Ba}_{0gydF4y2Ba}$ の物理的意味gydF4y2Ba

項gydF4y2Ba ${ωgydF4y2Ba}_{0gydF4y2Ba} tgydF4y2Ba$ は，“位相”gydF4y2Baと呼ばれます。余弦関数と正弦関数は，gydF4y2Ba $2gydF4y2Ba πgydF4y2Ba$ ごとに繰り返します。gydF4y2Ba ${ωgydF4y2Ba}_{0gydF4y2Ba} tgydF4y2Ba$ をgydF4y2Ba $2gydF4y2Ba πgydF4y2Ba$ だけ変化させるのに必要な時間は時間周期と呼ばれます。gydF4y2Ba

$TgydF4y2Ba ＝gydF4y2Ba \frac{2gydF4y2Ba πgydF4y2Ba}{{ωgydF4y2Ba}_{0gydF4y2Ba}} ＝gydF4y2Ba 2gydF4y2Ba πgydF4y2Ba \sqrt{\frac{rgydF4y2Ba}{ggydF4y2Ba}}$ ．gydF4y2Ba

時間周期gydF4y2Ba $TgydF4y2Ba$ は振子の長さの平方根に比例し，質量には依存しません。線形運動方程式では，時間周期は初期条件に依存しません。gydF4y2Ba

手順5:振子運動のプロットgydF4y2Ba

小角近似における振子の運動をプロットします。gydF4y2Ba

物理パラメ，タ，を定義します。gydF4y2Ba

重力加速度gydF4y2Ba $ggydF4y2Ba ＝gydF4y2Ba 9gydF4y2Ba ．gydF4y2Ba 8gydF4y2Ba 1gydF4y2Ba {米/秒gydF4y2Ba}^{2gydF4y2Ba}$
振子の長さgydF4y2Ba $rgydF4y2Ba ＝gydF4y2Ba 1gydF4y2Ba 米gydF4y2Ba$

gValue = 9.81;rValue = 1;omega_0Value = sqrt(gValue/rValue);T = 2*pi/omega_0Value;gydF4y2Ba

初期条件を設定します。gydF4y2Ba

theta_0Value = 0.1*pi;gydF4y2Ba%解只适用于小角度。gydF4y2Batheta_t0Value = 0;gydF4y2Ba最初处于静止状态。gydF4y2Ba

物理パラメ，タ，および初期条件を一般解に代入します。gydF4y2Ba

Vars = [omega_0 theta_0 theta_t0];values = [omega_0Value theta_0Value theta_t0Value];thetaSolPlot = subs(thetaSol,vars,values);gydF4y2Ba

調和振子運動をプロットします。gydF4y2Ba

fplot(thetaSolPlot(t* t)/pi， [0 5]);网格gydF4y2Ba在gydF4y2Ba；标题(gydF4y2Ba“谐摆运动”gydF4y2Ba）;包含(gydF4y2Ba“电汇”gydF4y2Ba）;ylabel (gydF4y2Ba“θ/ \ \π”gydF4y2Ba）;gydF4y2Ba

图中包含一个轴对象。标题为“谐波摆运动”的axis对象包含一个functionline类型的对象。gydF4y2Ba

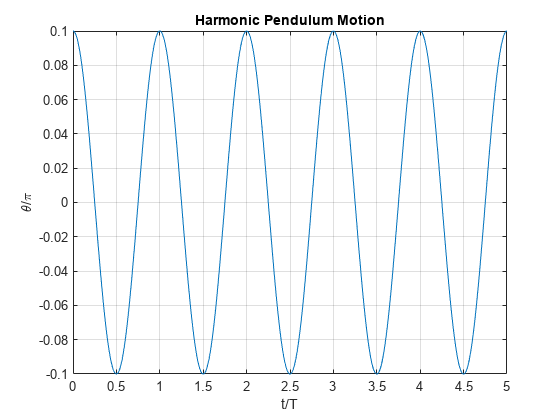
$θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba$ の解を求めた後，振子の運動を可視化します。gydF4y2Ba

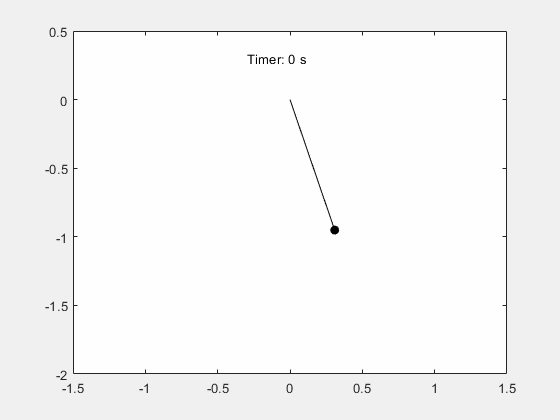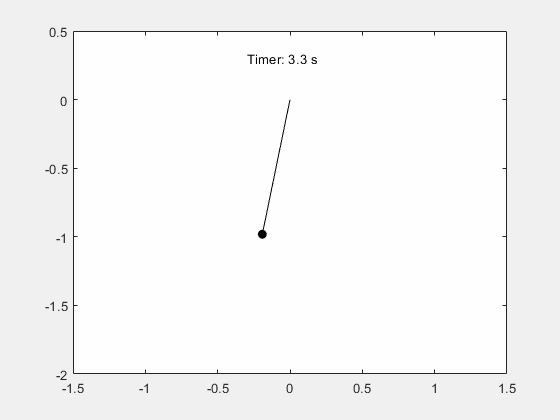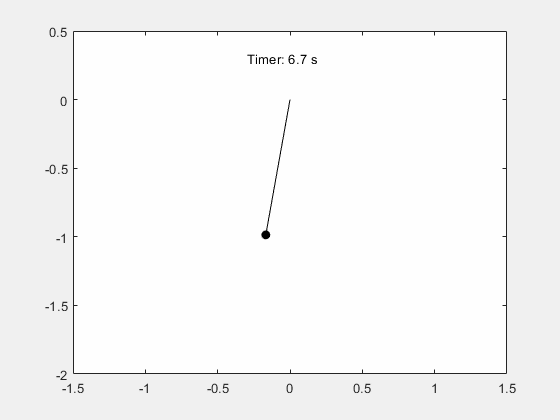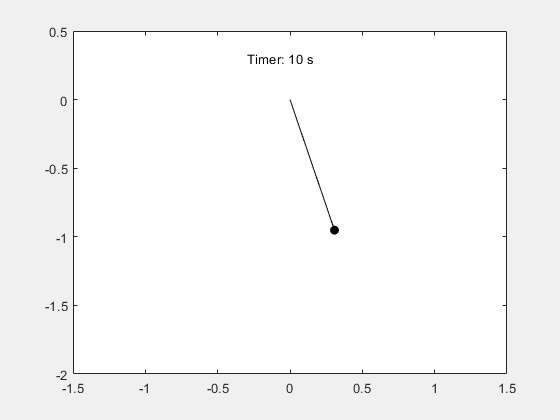
x_pos = sin(thetaSolPlot);y_pos = -cos(thetaSolPlot);fanimator (@fplot x_pos y_pos,gydF4y2Ba“柯”gydF4y2Ba，gydF4y2Ba“MarkerFaceColor”gydF4y2Ba，gydF4y2Ba“k”gydF4y2Ba，gydF4y2Ba“AnimationRange”gydF4y2Ba[0 5 * T]);持有gydF4y2Ba在gydF4y2Ba；fananimator (@(t) plot([0 x_pos(t)]，[0 y_pos(t)]，gydF4y2Ba“k -”gydF4y2Ba)，gydF4y2Ba“AnimationRange”gydF4y2Ba[0 5 * T]);fanimator (@ (t)文本(-0.3,0.3,gydF4y2Ba计时器:“gydF4y2Ba+ num2str (t, 2) +gydF4y2Ba“s”gydF4y2Ba)，gydF4y2Ba“AnimationRange”gydF4y2Ba[0 5 * T]);gydF4y2Ba

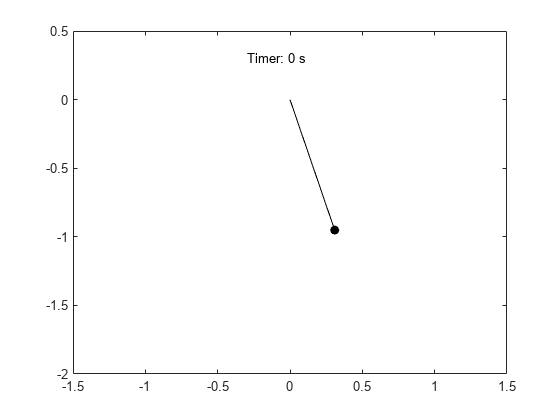
图中包含一个轴对象。axis对象包含3个参数化类型的对象:line, line, text。gydF4y2Ba

コマンドgydF4y2Ba那里gydF4y2Baを入力して振子運動のアニメ，ションを再生します。gydF4y2Ba

手順6:定エネルギ，軌道を使用した非線形振子運動の判別gydF4y2Ba

振子の非線形運動を理解するには，全エネルギ，の方程式を使用して振子の軌道を可視化します。全エネルギ，は保存されます。gydF4y2Ba

$EgydF4y2Ba ＝gydF4y2Ba \frac{1gydF4y2Ba}{2gydF4y2Ba} 米gydF4y2Ba {rgydF4y2Ba}^{2gydF4y2Ba} {（gydF4y2Ba \frac{dgydF4y2Ba θgydF4y2Ba}{dtgydF4y2Ba} ）gydF4y2Ba}^{2gydF4y2Ba} +gydF4y2Ba 米gydF4y2Ba ggydF4y2Ba rgydF4y2Ba （gydF4y2Ba 1gydF4y2Ba -gydF4y2Ba 因为gydF4y2Ba θgydF4y2Ba ）gydF4y2Ba$

三角恒等式gydF4y2Ba $1gydF4y2Ba -gydF4y2Ba 因为gydF4y2Ba θgydF4y2Ba ＝gydF4y2Ba 2gydF4y2Ba {罪gydF4y2Ba}^{2gydF4y2Ba} （gydF4y2Ba θgydF4y2Ba /gydF4y2Ba 2gydF4y2Ba ）gydF4y2Ba$ および関係gydF4y2Ba ${ωgydF4y2Ba}_{0gydF4y2Ba} ＝gydF4y2Ba \sqrt{ggydF4y2Ba /gydF4y2Ba rgydF4y2Ba}$ を使用して，スケ，リングされたエネルギ，を書き換えます。gydF4y2Ba

$\frac{EgydF4y2Ba}{米gydF4y2Ba {rgydF4y2Ba}^{2gydF4y2Ba}} ＝gydF4y2Ba \frac{1gydF4y2Ba}{2gydF4y2Ba} ［gydF4y2Ba {（gydF4y2Ba \frac{dgydF4y2Ba θgydF4y2Ba}{dtgydF4y2Ba} ）gydF4y2Ba}^{2gydF4y2Ba} +gydF4y2Ba {（gydF4y2Ba 2gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba} 罪gydF4y2Ba \frac{θgydF4y2Ba}{2gydF4y2Ba} ）gydF4y2Ba}^{2gydF4y2Ba} ］gydF4y2Ba$

エネルギ，は保存されるため，振子の運動は位相空間内の定エネルギ，軌道によって記述できます。位相空間は座標gydF4y2Ba $θgydF4y2Ba$ およびgydF4y2Ba $dgydF4y2Ba θgydF4y2Ba /gydF4y2Ba dgydF4y2Ba tgydF4y2Ba$ をも抽象空間です。これらの軌道をgydF4y2BafcontourgydF4y2Baを使用して可視化します。gydF4y2Ba

信谊gydF4y2BaθgydF4y2Batheta_tgydF4y2Baomega_0gydF4y2BaE(θ,theta_t omega_0) = (1/2) * (theta_t ^ 2 + (2 * omega_0 * sin(θ/ 2))^ 2);Eplot(， theta_t) = subs(E,omega_0,omega_0Value);图;fc = fcontour(Eplot(pi*theta, 2*omega_0Value*theta_t)， 2*[-1 1 -1 1]，gydF4y2Ba.．.gydF4y2Ba“线宽”gydF4y2Ba2,gydF4y2Ba“LevelList”gydF4y2Ba0:5:50,gydF4y2Ba“MeshDensity”gydF4y2Ba1 + 2 ^ 8);网格gydF4y2Ba在gydF4y2Ba；标题(gydF4y2Ba相空间中的恒能量等高线(\theta vs \theta_t)gydF4y2Ba）;包含(gydF4y2Ba“θ/ \ \π”gydF4y2Ba）;ylabel (gydF4y2Ba“\ theta_t / 2 \ omega_0”gydF4y2Ba）;gydF4y2Ba

图中包含一个轴对象。轴对象标题为C o n s ta n t空白E n r g y空白C o n t o u r s空白i n空白P h a s E空白s P a C E空白(空白theta空白v s。blank theta indexOf t baseline blank)包含一个函数轮廓类型的对象。gydF4y2Ba

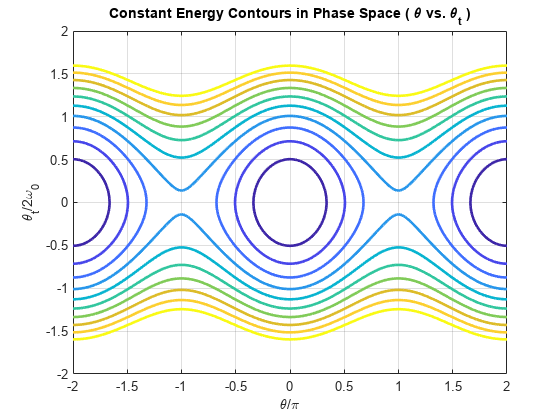
一定エネルギ，の等高線はgydF4y2Ba $θgydF4y2Ba$ 軸およびgydF4y2Ba $dgydF4y2Ba θgydF4y2Ba /gydF4y2Ba dgydF4y2Ba tgydF4y2Ba$ 軸に対して対称であり，gydF4y2Ba $θgydF4y2Ba$ 軸に沿って周期的です。2つの動作領域を図に示します。

等高線図の下側のエネルギ，は自身に近くなります。振子は2の最大角と最大速度の間で揺れます。振子の運動エネルギーは重力エネルギーに打ち勝つには十分ではなく,振子を完全に回転させることはできません。gydF4y2Ba

等高線図の上側のエネルギ，は自身に近づきません。振子は常に1の角度方向で運動します。振子の運動エネルギーは重力エネルギーに打ち勝つのに十分であり,振子を完全に回転させることができます。gydF4y2Ba

手順7:非線形運動方程式の求解gydF4y2Ba

非線形運動方程式は，2階微分方程式です。gydF4y2Ba数值gydF4y2Baソルバ，を使用して，これらの方程式を数値的に解きます。gydF4y2Ba数值gydF4y2Baは1次の系だけを受け入れるため，系を1次の系に簡約します。次に，gydF4y2Ba数值gydF4y2Baへの入力となる関数ハンドルを生成します。gydF4y2Ba

2階odeを1階ode系として書き換えます。gydF4y2Ba

信谊gydF4y2Baθ(t)gydF4y2Batheta_t (t)gydF4y2Baomega_0gydF4y2Ba= [diff(theta) == theta_t;Diff (theta_t) == -omega_0^2*sin(theta)]gydF4y2Ba

方程式(t) =gydF4y2Ba
                  
                    $（gydF4y2Ba \begin{array}{c} \frac{\partialgydF4y2Ba}{\partialgydF4y2Ba tgydF4y2Ba} θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ＝gydF4y2Ba {θgydF4y2Ba}_{tgydF4y2Ba} （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba \\ \frac{\partialgydF4y2Ba}{\partialgydF4y2Ba tgydF4y2Ba} {θgydF4y2Ba}_{tgydF4y2Ba} （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ＝gydF4y2Ba -gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba}^{2gydF4y2Ba} 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba \end{array} ）gydF4y2Ba$

eqs = subs(eqs,omega_0,omega_0Value);Vars = [theta, theta_t];gydF4y2Ba

系の質量行列gydF4y2Ba米gydF4y2Baおよび方程式gydF4y2BaFgydF4y2Baの右辺を含むベクトルを求めます。gydF4y2Ba

[M,F] = massMatrixForm(eqs,vars)gydF4y2Ba

M =gydF4y2Ba
                  
                    $（gydF4y2Ba \begin{array}{c} 1gydF4y2Ba & 0gydF4y2Ba \\ 0gydF4y2Ba & 1gydF4y2Ba \end{array} ）gydF4y2Ba$

F =gydF4y2Ba
                  
                    $（gydF4y2Ba \begin{array}{c} {θgydF4y2Ba}_{tgydF4y2Ba} （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba \\ -gydF4y2Ba \frac{981gydF4y2Ba 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba}{One hundred.gydF4y2Ba} \end{array} ）gydF4y2Ba$

米gydF4y2BaおよびgydF4y2BaFgydF4y2Baは次の形で表されます。gydF4y2Ba

$米gydF4y2Ba （gydF4y2Ba tgydF4y2Ba ，gydF4y2Ba xgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba \frac{dxgydF4y2Ba}{dtgydF4y2Ba} ＝gydF4y2Ba FgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ，gydF4y2Ba xgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba ．gydF4y2Ba$

後の計算を単純化するために，系を次の形に書き換えます。gydF4y2Ba $dgydF4y2Ba xgydF4y2Ba /gydF4y2Ba dgydF4y2Ba tgydF4y2Ba ＝gydF4y2Ba fgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ，gydF4y2Ba xgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba$ 。gydF4y2Ba

f = M\ fgydF4y2Ba

f =gydF4y2Ba
                  
                    $（gydF4y2Ba \begin{array}{c} {θgydF4y2Ba}_{tgydF4y2Ba} （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba \\ -gydF4y2Ba \frac{981gydF4y2Ba 罪gydF4y2Ba （gydF4y2Ba θgydF4y2Ba （gydF4y2Ba tgydF4y2Ba ）gydF4y2Ba ）gydF4y2Ba}{One hundred.gydF4y2Ba} \end{array} ）gydF4y2Ba$

odeFunctiongydF4y2Baを使用して，gydF4y2BafgydF4y2Baをmatlab関数ハンドルに変換します。結果の関数ハンドルはmatlab odeソルバgydF4y2Ba数值gydF4y2Baの入力になります。gydF4y2Ba

f = odeFunction(f, vars)gydF4y2Ba

f =gydF4y2BaFunction_handle with value:gydF4y2Ba@ (t, in2) [in2(2:);罪(in2(1:))。* 2./1.0 (-9.81 e + e + 2))gydF4y2Ba

手順8:閉じたエネルギ，等高線における運動方程式の求解gydF4y2Ba

数值gydF4y2Baを使用して，閉じたエネルギ，等高線のodeを解きます。gydF4y2Ba

エネルギ，等高線図から，閉じた等高線は条件gydF4y2Ba ${θgydF4y2Ba}_{0gydF4y2Ba} ＝gydF4y2Ba 0gydF4y2Ba$ 、gydF4y2Ba ${θgydF4y2Ba}_{tgydF4y2Ba 0gydF4y2Ba} /gydF4y2Ba 2gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba} \leqgydF4y2Ba 1gydF4y2Ba$ を満たします。gydF4y2Ba $θgydF4y2Ba$ およびgydF4y2Ba $dgydF4y2Ba θgydF4y2Ba /gydF4y2Ba dgydF4y2Ba tgydF4y2Ba$ の初期条件を変数gydF4y2Bax0gydF4y2Baに保存します。gydF4y2Ba

X0 = [0;1.99 * omega_0Value];gydF4y2Ba

解を求めるため，0秒から10秒までの時間間隔を指定します。この間隔で，振子は2周期分動くことができます。gydF4y2Ba

tInit = 0;tFinal = 10;gydF4y2Ba

Odeを解きます。gydF4y2Ba

sols = ode45(f，[tInit tFinal]，x0)gydF4y2Ba

溶胶=gydF4y2Ba带字段的结构:gydF4y2Ba求解器:'ode45' extdata: [1x1 struct] x: [0 3.2241e-05 1.9344e-04 9.9946e-04 0.0050 0.0252 0.1259…[y: [2x45 double] stats: [1x1 struct] idata: [1x1 struct]gydF4y2Ba

: sols.y (1)gydF4y2Baは角変位gydF4y2Ba $θgydF4y2Ba$ を表し，gydF4y2Ba: sols.y (2)gydF4y2Baは角速度gydF4y2Ba $dgydF4y2Ba θgydF4y2Ba /gydF4y2Ba dgydF4y2Ba tgydF4y2Ba$ を表します。gydF4y2Ba

閉じた軌道の解をプロットします。gydF4y2Ba

图;yyaxisgydF4y2Ba左gydF4y2Ba；情节(溶胶。x，: sols.y (1)，gydF4y2Ba“o”gydF4y2Ba）;ylabel (gydF4y2Ba“\θ(rad)”gydF4y2Ba）;yyaxisgydF4y2Ba正确的gydF4y2Ba；情节(溶胶。x，: sols.y (2)，gydF4y2Ba“o”gydF4y2Ba）;ylabel (gydF4y2Ba' \ theta_t (rad / s) 'gydF4y2Ba）;网格gydF4y2Ba在gydF4y2Ba；标题(gydF4y2Ba“相空间中的闭合路径”gydF4y2Ba）;包含(gydF4y2Ba“t (s)”gydF4y2Ba）;gydF4y2Ba

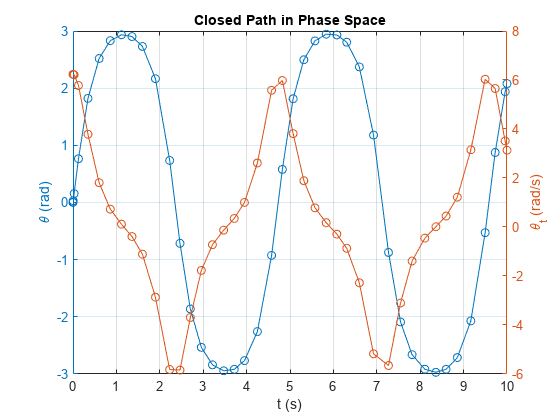
图中包含一个轴对象。在相空间中标题为封闭路径的axis对象包含2个类型为line的对象。gydF4y2Ba

振子の運動を可視化します。gydF4y2Ba

X_pos = @(t) sin(deval(sols,t,1));Y_pos = @(t) -cos(deval(sols,t,1));图;fanimator (@ (t)情节(x_pos (t) y_pos (t)gydF4y2Ba“柯”gydF4y2Ba，gydF4y2Ba“MarkerFaceColor”gydF4y2Ba，gydF4y2Ba“k”gydF4y2Ba));持有gydF4y2Ba在gydF4y2Ba；fananimator (@(t) plot([0 x_pos(t)]，[0 y_pos(t)]，gydF4y2Ba“k -”gydF4y2Ba));fanimator (@ (t)文本(-0.3,1.5,gydF4y2Ba计时器:“gydF4y2Ba+ num2str (t, 2) +gydF4y2Ba“s”gydF4y2Ba));gydF4y2Ba

图中包含一个轴对象。axis对象包含3个类型为line, text的对象。gydF4y2Ba

コマンドgydF4y2Ba那里gydF4y2Baを入力して振子運動のアニメ，ションを再生します。gydF4y2Ba

手順9:開いたエネルギ，等高線の解gydF4y2Ba

数值gydF4y2Baを使用して，開いたエネルギ，等高線のodeを解きます。エネルギ，等高線図から，開いた等高線は条件gydF4y2Ba ${θgydF4y2Ba}_{0gydF4y2Ba} ＝gydF4y2Ba 0gydF4y2Ba$ 、gydF4y2Ba ${θgydF4y2Ba}_{tgydF4y2Ba 0gydF4y2Ba} /gydF4y2Ba 2gydF4y2Ba {ωgydF4y2Ba}_{0gydF4y2Ba} >gydF4y2Ba 1gydF4y2Ba$ を満たします。gydF4y2Ba

X0 = [0;2.01 * omega_0Value];sols = ode45(f， [tInit, tFinal]， x0);gydF4y2Ba

開いたエネルギ，等高線の解をプロットします。gydF4y2Ba

图;yyaxisgydF4y2Ba左gydF4y2Ba；情节(溶胶。x，: sols.y (1)，gydF4y2Ba“o”gydF4y2Ba）;ylabel (gydF4y2Ba“\θ(rad)”gydF4y2Ba）;yyaxisgydF4y2Ba正确的gydF4y2Ba；情节(溶胶。x，: sols.y (2)，gydF4y2Ba“o”gydF4y2Ba）;ylabel (gydF4y2Ba' \ theta_t (rad / s) 'gydF4y2Ba）;网格gydF4y2Ba在gydF4y2Ba；标题(gydF4y2Ba“相空间中的开放路径”gydF4y2Ba）;包含(gydF4y2Ba“t (s)”gydF4y2Ba）;gydF4y2Ba

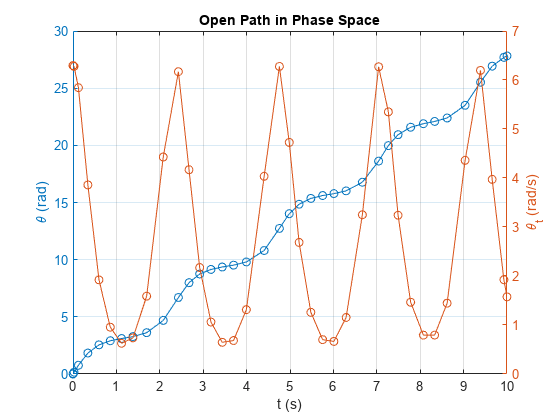
图中包含一个轴对象。在相空间中标题为Open Path的axis对象包含2个类型为line的对象。gydF4y2Ba

振子の運動を可視化します。gydF4y2Ba

X_pos = @(t) sin(deval(sols,t,1));Y_pos = @(t) -cos(deval(sols,t,1));图;fanimator (@ (t)情节(x_pos (t) y_pos (t)gydF4y2Ba“柯”gydF4y2Ba，gydF4y2Ba“MarkerFaceColor”gydF4y2Ba，gydF4y2Ba“k”gydF4y2Ba));持有gydF4y2Ba在gydF4y2Ba；fananimator (@(t) plot([0 x_pos(t)]，[0 y_pos(t)]，gydF4y2Ba“k -”gydF4y2Ba));fanimator (@ (t)文本(-0.3,1.5,gydF4y2Ba计时器:“gydF4y2Ba+ num2str (t, 2) +gydF4y2Ba“s”gydF4y2Ba));gydF4y2Ba

图中包含一个轴对象。axis对象包含3个类型为line, text的对象。gydF4y2Ba

コマンドgydF4y2Ba那里gydF4y2Baを入力して振子運動のアニメ，ションを再生します。gydF4y2Ba

振子の周期的揺れの動きのシミュレ，ションgydF4y2Ba

手順1:運動方程式の導出gydF4y2Ba

手順2:運動方程式の線形化gydF4y2Ba

手順3:運動方程式の解析的な求解gydF4y2Ba

手順 4:gydF4y2Ba ωgydF4y2Ba 0gydF4y2Ba の物理的意味gydF4y2Ba

手順5:振子運動のプロットgydF4y2Ba

手順6:定エネルギ，軌道を使用した非線形振子運動の判別gydF4y2Ba

手順7:非線形運動方程式の求解gydF4y2Ba

手順8:閉じたエネルギ，等高線における運動方程式の求解gydF4y2Ba

手順9:開いたエネルギ，等高線の解gydF4y2Ba

手順 4:gydF4y2Ba ${ωgydF4y2Ba}_{0gydF4y2Ba}$ の物理的意味gydF4y2Ba