主要内容
量化系统的绝对稳定性
这个例子说明了当一个线性定常系统与一个属于圆锥扇区的静态非线性系统处于反馈互联时,如何增强系统的绝对稳定性。
反馈连接
考虑如图1所示的反馈连接。

图1:反馈连接
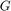 是线性时不变系统吗
是线性时不变系统吗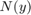 是属于圆锥扇形的静态非线性
是属于圆锥扇形的静态非线性![[\α,β\]美元](http://www.tianjin-qmedu.com/nl/help/examples/control/win64/AbsoluteStabilityForQuantizedSystemExample_eq17999177181437605090.png) (
(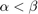 );也就是说,
);也就是说,
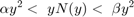
对于这个示例,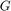 为下面的离散时间系统。
为下面的离散时间系统。
目录(fullfile (matlabroot,“例子”,“控制”,“主要”))%添加示例数据A=[0.9995,0.0100,0.0001;-0.0020,0.9995,0.0106;0,0,0.9978];B=[0,0.002,0.04]';C=[2.3948,0.3303,2.2726];D=0;G=ss(A,B,C,D,0.01);
部门有界非线性
在这个例子中,非线性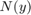 为对数量化器,其定义如下:
为对数量化器,其定义如下:
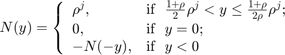
在那里,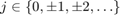 .这个量化器属于扇区范围
.这个量化器属于扇区范围![{frac2}\rho1+{frac2}\rho1]$](http://www.tianjin-qmedu.com/nl/help/examples/control/win64/AbsoluteStabilityForQuantizedSystemExample_eq05936810714490360334.png) .例如,如果
.例如,如果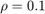 ,则量化器属于二次曲线扇区[0.1818,1.8182]。
,则量化器属于二次曲线扇区[0.1818,1.8182]。
%量化器参数ρ= 0.1;%下界α=2*rho/(1+rho)%上界β= 2 /(1 +ρ)
Alpha = 0.1818 beta = 1.8182
绘制量化器的扇区边界。
绘图仪扇区边界(rho)

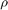 表示量化密度,其中
表示量化密度,其中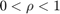 .如果
.如果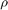 值越大,则量化值越精确。有关此量化器的详细信息,请参阅[1]。
值越大,则量化值越精确。有关此量化器的详细信息,请参阅[1]。
绝对稳定的圆锥扇形条件
量化器的圆锥扇形矩阵由下式给出
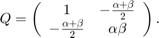
为了保证图1中反馈连接的稳定性,线性系统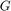 需要满足
需要满足
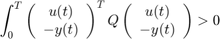
在那里, 和
和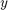 输入和输出是
输入和输出是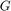 ,分别。
,分别。
这种情况可以通过检查扇区指数,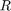 ,小于
,小于1.
用定义量化器的圆锥扇形矩阵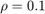 .
.
Q =(1 -(α+β)/ 2,-(α+β)/ 2,αβ*);
获得的扇区指数问和G.
R=getSectorIndex([1;-G],-Q)
R = 1.8247
自从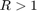 ,闭环系统不稳定。要查看这种不稳定性,请使用下面的Simulink模型。万博1manbetx
,闭环系统不稳定。要查看这种不稳定性,请使用下面的Simulink模型。万博1manbetx
mdl =“DTQuantization”;open_system (mdl)

运行Simuli万博1manbetxnk模型。
sim (mdl) open_system (“DTQuantization /输出”)
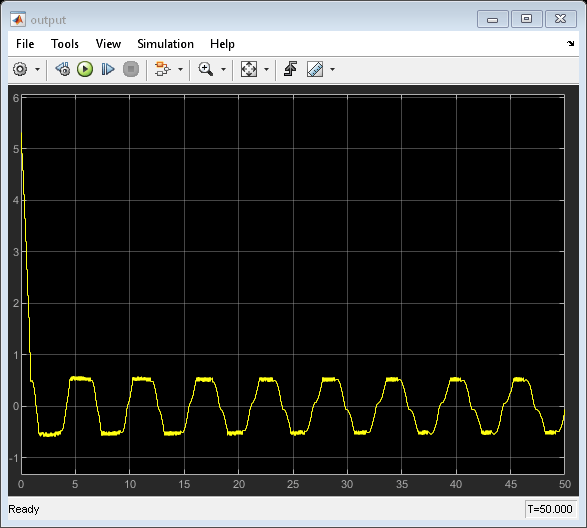
从输出轨迹可以看出闭环系统是不稳定的。这是因为量子器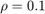 太粗了。
太粗了。
增加量子化密度,让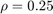 .量化器属于圆锥扇区[0.4,1.6]。
.量化器属于圆锥扇区[0.4,1.6]。
%量化器参数ρ= 0.25;%下界α=2*rho/(1+rho)%上界β= 2 /(1 +ρ)
Alpha = 0.4000 beta = 1.6000
绘制量化器的扇区边界。
绘图仪扇区边界(rho)
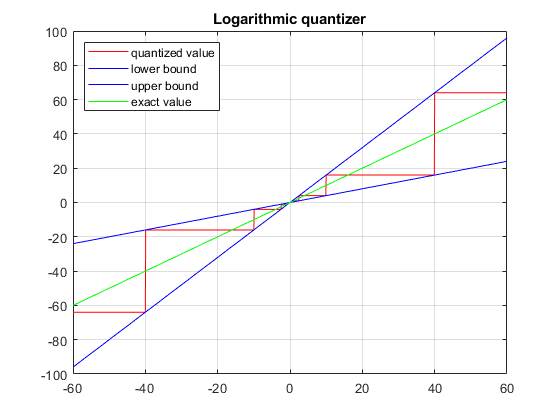
用定义量化器的圆锥扇形矩阵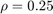 .
.
Q =(1 -(α+β)/ 2,-(α+β)/ 2,αβ*);
获得的扇区指数问和G.
R=getSectorIndex([1;-G],-Q)
R=0.9702
量化器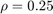 满足反馈连接稳定性的二次扇形条件
满足反馈连接稳定性的二次扇形条件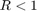 .
.
使用下列工具运行万博1manbetxSimulink模型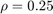 .
.
sim (mdl) open_system (“DTQuantization /输出”)

从扇区指数可以看出,闭环系统是稳定的。
参考
[1]傅M.,谢磊,“量子化反馈控制的扇形界方法”,自动控制学报50(11), 2005年,1698 - 1711。
bdclose (mdl);rmpath (fullfile (matlabroot,“例子”,“控制”,“主要”))%删除示例数据