Logistic回归模型的贝叶斯分析

打开脚本

这个例子展示了如何对逻辑回归模型进行贝叶斯推理slicesample．

统计推断通常基于最大似然估计(MLE)。MLE选择使数据的可能性最大化的参数，直观上很吸引人。在MLE中，假设参数是未知的但固定的，并具有一定的置信度估计。在贝叶斯统计中，未知参数的不确定性用概率来量化，将未知参数视为随机变量。

贝叶斯推理

贝叶斯推理是结合模型或模型参数的先验知识来分析统计模型的过程。这种推论的根源是贝叶斯定理:

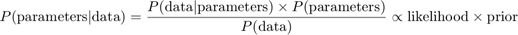
$P(\mathrm{参数|数据})= \frac {P(\mathrm{数据|参数})\times P(\mathrm{参数})} {P (\ mathrm{数据})}& # xA;\propto \mathrm{likelihood} \times \mathrm{prior}$

例如，假设我们有正常的观察结果

$X|\theta \sim N(\theta， \sigma^2)$

是已知的，先验分布是

$\theta \sim N(\mu， \tau^2)$

在这个公式中，和，有时被称为超参数，也是已知的。如果我们观察n的样本X，我们可以得到as的后验分布

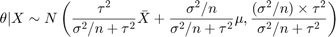
$$ \θ| X \ sim N \离开(\压裂{\τ^ 2}{\σ^ 2 / N + \ t ^ 2} \酒吧X + & # xA;\压裂{\σ^ 2 / n}{{\σ^ 2 / n + \ t ^ 2}} \μ,& # xA;\压裂{(\σ^ 2 / n) \ \τ^ 2}{\σ^ 2 / n + & # xA;\τ^ 2}\ $$

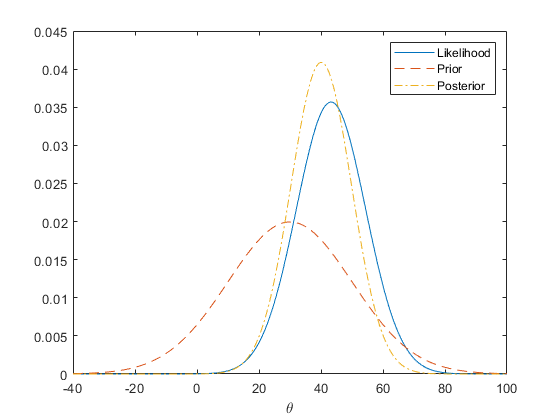
下面的图表显示了的先验，可能性和后验。

rng (0,“旋风”）;N = 20;Sigma = 50;X = normrnd(10,sigma,n,1);Mu = 30;Tau = 20;Theta = linspace(- 40,100,500);Y1 = normpdf(mean(x)，theta,sigma/√(n));Y2 = normpdf(theta,mu,tau);postMean =τ^ 2 *意味着(x) /(τ)^ 2 +σ^ 2 / n) +σ^ 2 *亩/ n /(τ)^ 2 +σ^ 2 / n); postSD = sqrt(tau^2*sigma^2/n/(tau^2+sigma^2/n)); y3 = normpdf(theta, postMean,postSD); plot(theta,y1,“- - -”θ,y2,“——”,θ,y3,“-”。)传说(“可能性”，“之前”，“后”)包含(‘\θ）

汽车实验数据

在一些简单的问题中，如前面的正态均值推断例子，很容易以封闭的形式求出后验分布。但在涉及非共轭先验的一般问题中，后验分布很难或不可能用解析方法计算。我们将考虑逻辑回归作为一个例子。这个例子涉及到一个实验，以帮助建模各种重量的汽车在里程测试中失败的比例。数据包括对重量的观察，测试的汽车数量和失败的数量。我们将使用权重的转换版本，以减少回归参数估计中的相关性。

一套汽车砝码重量= [2100 2300 2500 2700 2900 3100 3300 3500 3700 3900 4100 4300]';重量= (Weight -2800)/1000;%重新集中和缩放每种重量测试的汽车数量。%Total = [48 42 31 34 31 21 23 23 21 16 17 21]';在每个重量下，每加仑行驶里程表现不佳的汽车数量。%Poor = [1 2 0 3 8 8 14 17 19 15 17 21]';

Logistic回归模型

逻辑回归是广义线性模型的一种特殊情况，适用于这些数据，因为响应变量是二项的。逻辑回归模型可以写成:

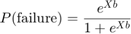
$P(\ mathm {failure}) = \frac{e^{Xb}}{1+e^{Xb}}$

其中X是设计矩阵，b是包含模型参数的向量。在MATLAB®中，我们可以将这个方程写成:

logitp = @ (b, x) exp (b(1) +(2)。* x) / (1 + exp (b(1) +(2)。* x));

如果你有一些先验知识或一些可用的非信息性先验，你可以指定模型参数的先验概率分布。例如，在这个例子中，我们使用正常先验进行拦截b1和斜率b2,即

Prior1 = @(b1) normpdf(b1,0,20);截距先验%Prior2 = @(b2) normpdf(b2,0,20);斜率先验%

根据贝叶斯定理，模型参数的联合后验分布与似然和先验的乘积成正比。

Post = @(b) prod(binopdf(poor,total,logitp(b,weight)))).．.%的可能性* prior1(b(1)) * prior2(b(2));%先验

注意，在这个模型中，后验的归一化常数在解析上是难以处理的。然而，即使不知道归一化常数，如果你知道模型参数的大致范围，你也可以看到后验分布。

B1 = linspace(-2.5， - 1,50);B2 = linspace(3, 5.5, 50);Simpost = 0 (50,50);为I = 1:长度(b1)为j = 1:长度(b2) simpost后(i, j) = ((b1(我),b2 (j)]);结束；结束；网格(b2, b1, simpost)包含(“坡”) ylabel (“拦截”) zlabel (“后验密度”)视图(-110,30)

这个后验在参数空间中沿着对角线被拉长，这表明，在我们查看数据后，我们相信参数是相关的。这很有趣，因为在我们收集任何数据之前，我们假设它们是独立的。相关性来自于我们的先验分布和似然函数的结合。

片抽样

蒙特卡罗方法常用于贝叶斯数据分析，以总结后验分布。其思想是，即使你不能分析地计算后验分布，你也可以从分布中生成一个随机样本，并使用这些随机值来估计后验分布或派生的统计数据，如后验平均值、中位数、标准差等。切片采样是一种设计用于从具有任意密度函数的分布中采样的算法，该分布仅已知比例常数，这正是从一个归一化常数未知的复杂后验分布中采样所需要的。该算法不生成独立样本，而是生成平稳分布为目标分布的马尔可夫序列。因此，切片采样器是一种马尔科夫链蒙特卡洛(MCMC)算法。然而，它与其他著名的MCMC算法不同，因为只需要指定缩放后验——不需要提议或边际分布。

本例展示了如何使用切片采样器作为里程测试逻辑回归模型贝叶斯分析的一部分，包括从模型参数的后验分布中生成随机样本，分析采样器的输出，以及对模型参数进行推断。第一步是生成一个随机样本。

Initial = [1 1];Nsamples = 1000;Trace = slicesample(initial,nsamples，“pdf”的帖子,“宽度”20 [2]);

采样器输出分析

从切片采样器中获得随机样本后，重要的是研究收敛性和混合等问题，以确定样本是否可以合理地视为来自目标后验分布的随机实现集。查看边缘轨迹图是检查输出的最简单方法。

Subplot (2,1,1) plot(trace(:，1))“拦截”）;Subplot (2,1,2) plot(trace(:，2)) ylabel(“坡”）;包含(的样本数量）;

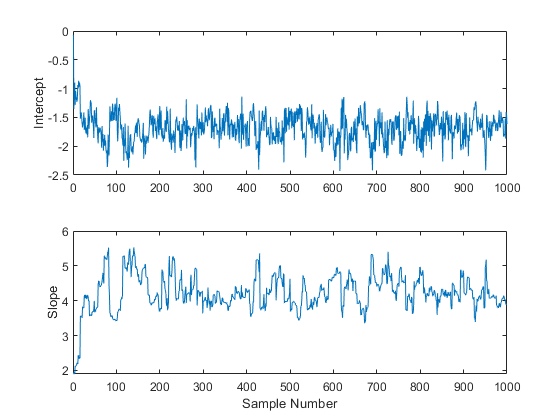
从这些图中可以明显看出，参数起始值的影响需要一段时间才能消失(也许是50个左右的样本)，然后过程才开始看起来稳定。

在检查收敛性时，使用移动窗口计算统计数据(如样本均值、中位数或样本标准偏差)也很有帮助。这比原始样本轨迹产生更平滑的图形，并且可以更容易地识别和理解任何非平稳性。

Movavg = filter((1/50)*ones(50,1)， 1, trace);Subplot (2,1,1) plot(movavg(:，1)) xlabel(“样本数量”) ylabel (“拦截手段”）;Subplot (2,1,2) plot(movavg(:，2)) xlabel(“样本数量”) ylabel (“斜率均值”）;

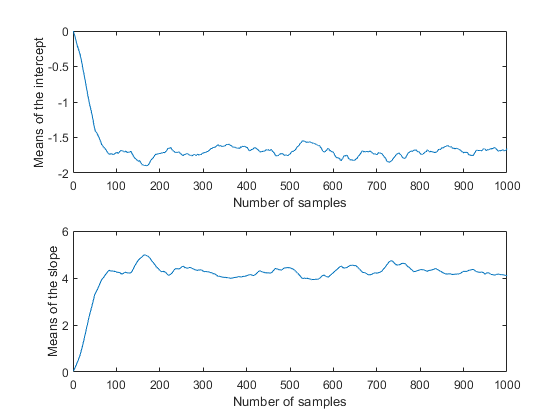
因为这些是50次迭代窗口的移动平均值，所以前50个值与图的其余部分是不可比较的。然而，每个图的其余部分似乎证实了参数后验均值在100次左右迭代后收敛到平稳。同样明显的是，这两个参数是相互关联的，与前面的后验密度图一致。

由于适应期代表的样本不能被合理地视为来自目标分布的随机实现，因此最好不要在切片采样器输出的开始使用前50个左右的值。您可以删除输出的这些行，但是，也可以指定“老化”时期。当已经知道合适的老化长度时，这是很方便的。

Trace = slicesample(initial,nsamples，“pdf”的帖子,.．.“宽度”20 [2],“燃烧”, 50);Subplot (2,1,1) plot(trace(:，1))“拦截”）;Subplot (2,1,2) plot(trace(:，2)) ylabel(“坡”）;

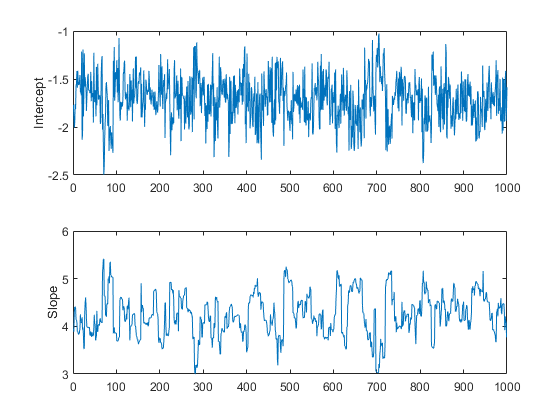
这些轨迹图似乎没有显示出任何非平稳，表明老化期已经完成了它的工作。

然而，跟踪图的第二个方面也应该加以探讨。虽然截距的轨迹看起来像高频噪声，但斜率的轨迹似乎具有较低的频率成分，这表明相邻迭代的值之间存在自相关性。我们仍然可以从这个自相关样本中计算平均值，但通过去除样本中的冗余来减少存储需求通常是很方便的。如果这消除了自相关，它也将允许我们将其视为独立值的样本。例如，您可以通过只保留每10个值来稀释样本。

Trace = slicesample(initial,nsamples，“pdf”的帖子,“宽度”20 [2],.．.“燃烧”, 50岁,“薄”10);

为了检查这种细化的效果，从迹线估计样本自相关函数并使用它们来检查样本是否快速混合是有用的。

F = fft(趋势(跟踪，“不变”));F = F .* conj(F);ACF = ifft(F);Acf = Acf (1:21，:);%保留延迟高达20。ACF = real([ACF(1:21,1) ./ ACF(1,1)).．.Acf (1:21,2) ./ Acf (1,2)]);%正常化。边界=√(1/nsamples) * [2;2);% 95% CI为iid正常实验室= {“拦截ACF样本”，“斜坡的ACF样本”};为lineHandles = stem(0:20, ACF(:，i)，“填充”，“r-o”）;lineHandles。MarkerSize = 4;网格(“上”)包含(“滞后”) ylabel(实验室{i}) hold住在图([0.5 0.5;20 20]， [bounds([1 1])) bounds([2 2])]，“- b”）;Plot ([0 20]， [0 0]，“- k”）;持有从A =轴;轴([1](1:3));结束

第一个滞后处的自相关值对于截距参数很重要，对于斜率参数更是如此。我们可以使用更大的细化参数重复采样，以进一步降低相关性。但是，为了本例的目的，我们将继续使用当前示例。

模型参数的推断

正如预期的那样，样本的直方图模拟了后验密度图。

次要情节(1,1,1)hist3(跟踪,(25、25));包含(“拦截”) ylabel (“坡”) zlabel (“后验密度”)视图(-110,30)

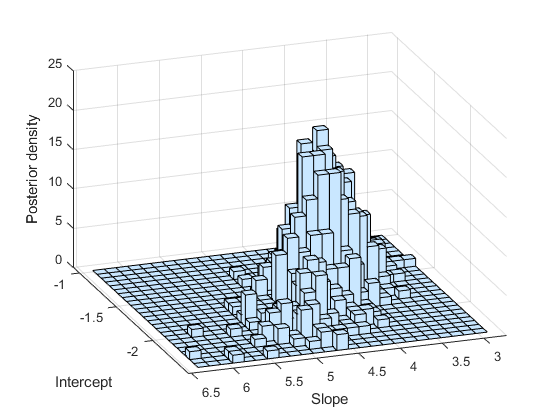
您可以使用直方图或核平滑密度估计来总结后验样本的边缘分布特性。

Subplot (2,1,1) hist(trace(:，1)) xlabel(“拦截”）;Subplot (2,1,2) ksdensity(trace(:，2)) xlabel(“坡”）;

您还可以计算描述性统计数据，例如随机样本的后验平均值或百分位数。要确定样本量是否足够大，以达到所需的精度，监测作为样本数函数的所需迹的统计量是有帮助的。

Csum = cumsum(trace);次要情节(2,1,1)情节(csum(: 1)“。/ (1:nsamples))包含(“样本数量”) ylabel (“拦截手段”）;次要情节(2,1,2)情节(csum(:, 2)’。/ (1:nsamples))包含(“样本数量”) ylabel (“斜率均值”）;

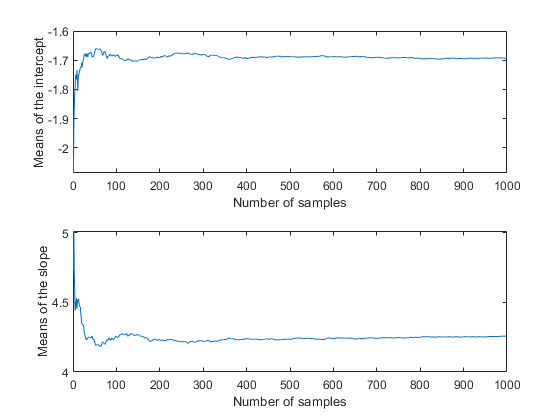
在这种情况下，1000的样本量似乎足以为后验平均估计提供良好的精度。

bHat = mean(trace)

bHat = -1.6931 4.2569

总结

统计和机器学习工具箱™提供了各种功能，允许您轻松指定可能性和先验。它们可以结合起来得到后验分布。的slicesample函数使您可以在MATLAB中使用马尔可夫链进行贝叶斯分析蒙特卡罗仿真。它甚至可以用于带有后验分布的问题，这些问题很难从标准随机数生成器中进行抽样。