尺度函数与小波

本例使用波风演示双正交滤波器对中消失矩的个数如何影响相应的对偶尺度函数和小波的平滑性。本示例使用了波风对于双正交小波，“bior3.7”，你也可以用波风获得正交尺度函数和小波函数。

首先，获得尺度和小波滤波器，并查看在小波的消失矩的数量。这等价于观察双滤波器中-1+i0处的0个数。

[LoD、藏、卤,HiR] = wfilters (“bior3.7”）;

如果您有信号处理工具箱™，您可以使用zplane查看分解和重构过滤器在-1+i0处的零数。

Z平面（LoD）；标题(分解滤波器的）;

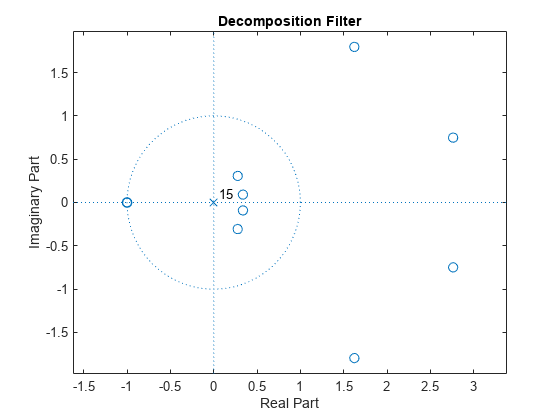
图形；Z平面（LoR）；标题(“重建过滤器”）;

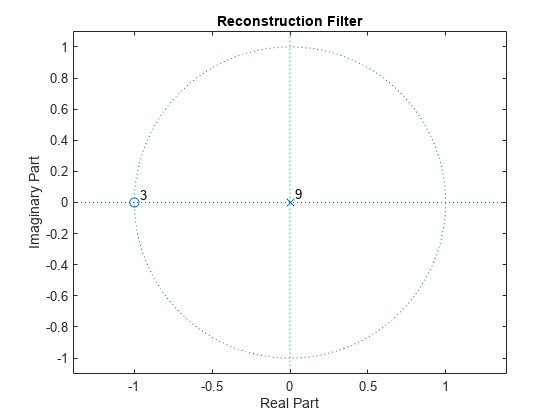
如果你放大-1+i0附近的区域，你会发现分解滤波器中有7个零，重构滤波器中有3个零。这对相应尺度函数和小波的平滑性有重要的影响。对于双正交小波，低通滤波器中-1+i0处的零越多，滤波器越平滑相反为尺度函数和小波。换句话说，分解滤波器中的更多的零意味着更平滑的重构尺度函数和小波。相反，在重建滤波器中，更多的零意味着更平滑的分解尺度函数和小波。

使用波风证实了这一点。对于正交和双正交小波，波风通过反转Mallat算法工作。具体而言，该算法从最粗分辨率级别的单个小波或尺度系数开始，并将小波或尺度函数重建到指定的最细分辨率级别。通常，8到10个级别就足以获得尺度函数和小波的精确表示。

[phiD, psiD,什么稀罕,psiR] = wavefun (“bior3.7”10);次要情节(2,1,1)情节([phiD '什么稀罕']);网格在…上; 头衔(“Bior3.7扩展函数”); 传奇(“分解”，“重建”）;次要情节(2,1,2)情节([psiD ' psiR ']);网格在…上; 头衔(“Bior3.7小波”); 传奇(“分解”，“重建”）;

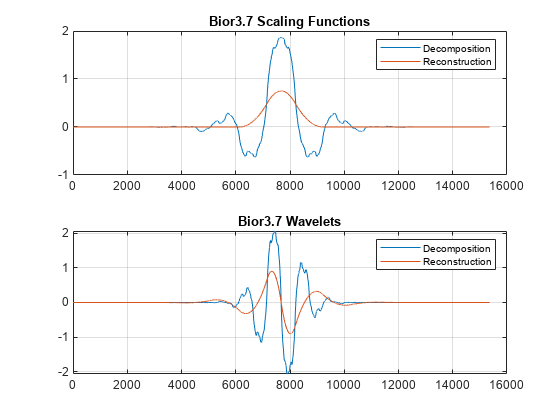
由于低通分解滤波器在-1+i0处的零数是低通分解滤波器的两倍以上，因此，对偶(重构)尺度函数和小波比分析(分解)尺度函数和小波平滑得多。