拟合Diebold-Li模型
本例显示了如何构建1990年至2010年每个月美国收益率曲线的Diebold-Li模型。该示例还演示了如何通过将自回归模型拟合到每个参数的时间序列来预测未来收益率曲线。
该文件可在此处找到:
https://www.nber.org/papers/w10048
加载数据
使用的数据是1990年至2010年的月度国债收益率,期限为1个月、3个月、6个月、1年、2年、3年、5年、7年、10年、20年、30年。
每日数据可在此处找到:
数据作为MATLAB文件存储在MATLAB®数据文件中数据集对象
负载数据曲线%提取每月最后一天的数据MonthYearMat=repmat((1990:2010)”,1,12)”;EOMDates=lbusdate(MonthYearMat(:),repmat((1:12)”,21,1));MonthlyIndex=find(ismember(Dataset.Properties.ObsNames,datestr(EOMDates));Estimationdataset=Dataset(MonthlyIndex,:);EstimationData=double(Estimationdataset);
迪堡-李模型
Diebold和Li从Nelson Siegel模型开始
并将其改写为以下内容:
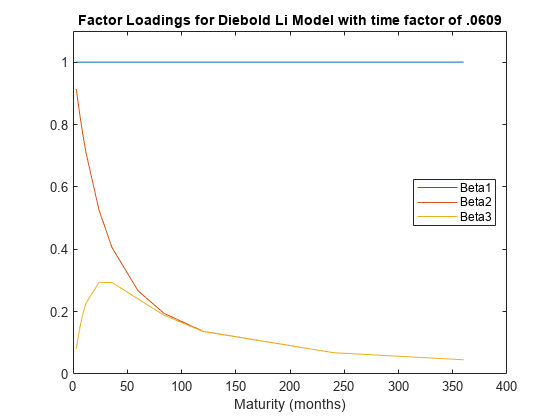
上述模型允许按以下方式解释这些因素:Beta1对应于收益率曲线的长期/水平,Beta2对应于短期/斜率,Beta3对应于中期/曲率。 确定曲率上的载荷最大化的成熟度,并控制模型的指数衰减率。
迪博尔德和李彦宏倡导环境 在30个月时最大化中期因子Beta3的负荷。这也将问题从非线性拟合转化为简单的线性回归。
%显式设置时间因子lambdalambda_t=.0609;%构造因子载荷矩阵%与数据相关的期限TimeToMat=[3691224366084120240360];X=[one(size(TimeToMat))(1-exp(-lambda_t*TimeToMat))。/(lambda_t*TimeToMat)...((1-exp(-lambda_t*TimeToMat))。/(lambda_t*TimeToMat)-exp(-lambda_t*TimeToMat));%绘制因子负荷图绘图(计时器,X)标题(“Diebold-Li模型的因子载荷,时间因子为.0609”)xlabel(‘到期日(月)’)ylim([0 1.1])图例({“Beta1”,“β2”,“Beta3”},“位置”,“东方”)
符合模型
A.迪博尔德利对象的开发有助于从产量数据拟合模型迪博尔德利对象继承自圆曲线对象,所以getZeroRates,获取折扣因素,GetParyiels,getForwardRates,及toRateSpec方法都已实现fitYieldsFromBetas在给定lambda参数的情况下,对观测到的市场收益率进行贝塔参数估计。
这个迪博尔德利对象用于拟合从1990年到2010年每个月的Diebold Li模型。
%预先分配贝塔β=零(大小(估计数据,1),3);%循环并拟合每个月末的收益率曲线对于jdx=1:size(EstimationData,1)tmpCurveModel=DieboldLi.fitbetas from收益率(eomdate(jdx),lambda_t*12,daysad(eomdate(jdx),30*TimeToMat),EstimationData(jdx,:);Beta(jdx,:)=[tmpCurveModel.Beta1 tmpCurveModel.Beta2 tmpCurveModel.Beta3];结束
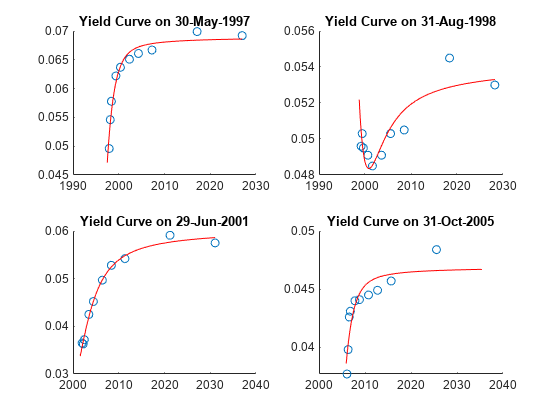
Diebold Li适合选定日期,包括在此处
PlotSettles=datenum({‘1997年5月30日’,‘1998年8月31日’,‘2001年6月29日’,‘2005年10月31日’}); 图形对于jdx=1:length(PlotSettles)subplot(2,2,jdx)tmpIdx=find(strcmpi(Estimationdataset.Properties.ObsNames,datestr(PlotSettles(jdx));tmpCurveModel=DieboldLi.fitBetasFromYields(PlotSettles(jdx),lambda_t*12,...daysadd(PlotSettles(jdx),30*TimeToMat),EstimationData(tmpIdx,:)';scatter(daysadd(PlotSettles(jdx),30*TimeToMat),EstimationData(tmpIdx,:))保持在…上PlottingDates=(PlottingSettles(jdx)+30:30:PlottingSettles(jdx)+30*360);(PlottingDates,tmpCurveModel.getParYields(PlottingDates),“r-”)头衔([“收益率曲线”datestr(PlotSettles(jdx))])datetick结束
预测
Diebold-Li模型可用于预测未来收益率曲线。Diebold和Li建议将AR(1)模型拟合到每个贝塔参数的时间序列中。然后,该拟合模型可用于预测每个参数的未来值,进而预测未来收益率曲线。
对于本例,使用MATLAB函数倒退用于估计每个β的AR(1)模型的参数。
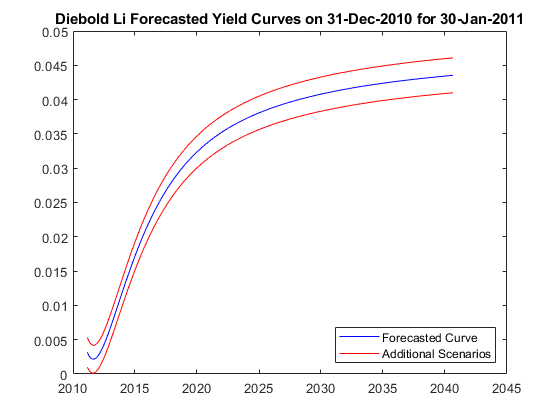
回归拟合的置信区间也用于生成两个附加收益率曲线预测,作为收益率曲线的附加可能场景。
这个月滞可以调整变量以进行不同的期前预测。例如,将值从1.到6.将预测从提前1个月更改为提前6个月。
月间隔=1;[tmpBeta,bint]=回归(β(月间隔+1:end,1),[1(月间隔+1:end,1))β(月间隔+1:end,1)];预测贝塔(1,1)=[1贝塔(结束,1)]*tmpBeta;预测贝塔(1,1)=[1贝塔(结束,1)]*bint(:,1);预测贝塔(1,1)=[1贝塔(结束,1)]*bint(:,2);[tmpBeta,bint]=回归(β(月间隔+1:end,2),[1(月间隔+1:end,2))β(月间隔+1:end,2)];预测贝塔(1,2)=[1贝塔(结束,2)]*tmpBeta;预测贝塔(1,2)=[1贝塔(结束,2)]*bint(:,1);预测贝塔(1,2)=[1贝塔(结束,2)]*bint(:,2);[tmpBeta,bint]=回归(β(月间隔+1:end,3),[1(月间隔+1:end,3))β(月间隔+1:end,3)];预测贝塔(1,3)=[1贝塔(结束,3)]*tmpBeta;预测贝塔(1,3)=[1贝塔(结束,3)]*bint(:,1);预测贝塔(1,3)=[1贝塔(结束,3)]*bint(:,2);%预测收益率曲线数字结算=日结算(EOMDates(end),30*个月滞后;DieboldLi_预测=DieboldLi(“帕尔利德”,结算,[ForecastBeta lambda_t*12]);迪博尔德利(DieboldLi_Forecast_Up=DieboldLi(“帕尔利德”,结算,[ForecastBeta_Up lambda_t*12]);DieboldLi_Forecast_Down=DieboldLi(“帕尔利德”,结算,【预报员贝塔·唐·兰姆达·t*12】;绘图日期=(结算+30:30:结算+30*360);绘图(绘图日期,DieboldLi_Forecast.getParYields(绘图日期),“b-”)持有在…上绘图(绘图日期,DieboldLi\u Forecast\u Up.getParYields(绘图日期),“r-”)绘图(绘图日期,DieboldLi\u预测值\u下降。getParYields(绘图日期),“r-”)头衔([“Diebold Li预测的收益率曲线”日期(EOMDates(end))“为了”日期(结算)])图例({“预测曲线”,“其他场景”},“位置”,‘东南’)datetick
参考文献
此示例基于以下文件:
[1] Francis X.Diebold,Canlin Li,《预测政府债券收益率的期限结构》,计量经济学杂志,第130卷,第2期,2006年2月,第337-364页

