线性卡尔曼滤波器

当使用卡尔曼滤波器来跟踪对象，则使用检测或测量的顺序来构造对象运动的模型。对象运动是由物体的状态的演变限定。卡尔曼滤波器是一个最佳的，递归算法用于估计目标的轨道。该过滤器是递归的，因为它使用了以前的状态，使用可能已在间隔取得测量更新当前的状态。卡尔曼滤波器采用了这些新的测量，以保持状态估计尽可能准确。该过滤器是最佳的，因为它最大限度地减少国家的均方误差。您可以使用过滤器来预测未来的状态或估计当前状态或过去的状态。

状态方程

对于传感器融合和跟踪工具箱™中跟踪的大多数类型的对象，状态向量由一个、两个或三维位置和速度组成。

从运动物体的牛顿方程开始X- 方向以恒定的加速度和这些方程转换为空间状态形式。

米 X ¨ = F X ¨ = F 米 = 一个

如果定义状态

X 1 = X X 2 = X ˙ ，

你可以把牛顿定律写成状态空间的形式。

d d Ť [ X 1 X 2 ] = [ 0 1 0 0 ] [ X 1 X 2 ] + [ 0 1 ] 一个

您使用的线性动态模型，当你有信心，对象遵循该类型的运动。有时模型包括过程噪声反映在运动模式的不确定性。在这种情况下，牛顿方程有一个附加项。

d d Ť [ X 1 X 2 ] = [ 0 1 0 0 ] [ X 1 X 2 ] + [ 0 1 ] 一个 + [ 0 1 ] v ķ

vķ为加速度的未知噪声摄动。只有噪音的统计数据是已知的。假设为零均值高斯白噪声。

您可以在此类型的方程扩展到多个维度。在两个维度中，方程式的形式为

d d Ť [ X 1 X 2 ÿ 1 ÿ 2 ] = [ 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 ] [ X 1 X 2 ÿ 1 ÿ 2 ] + [ 0 一个 X 0 一个 ÿ ] + [ 0 v X 0 v ÿ ]

右边的4×4矩阵是状态转换模型矩阵。独立X-和y -运动，这是矩阵块对角。

当转换到离散时间，你整合在所述时间间隔的长度的运动方程。在离散的形式，对于一个采样间隔Ť，则状态表示形式变为

[ X 1 ， ķ + 1 X 2 ， ķ + 1 ] = [ 1 Ť 0 1 ] [ X 1 ， ķ X 2 ， ķ ] + [ 0 Ť ] 一个 + [ 0 1 ] v ˜

的数量Xk + 1状态是离散时间的吗k + 1,Xķ是早期离散时间下的状态，ķ。如果包括噪声，方程变得更加复杂，因为噪音的整合并不简单。

状态方程可以推广到

X ķ + 1 = F ķ X ķ + G ķ ü ķ + v ķ

Fķ状态转移矩阵和Gķ是控制矩阵。控制矩阵考虑到作用在物体上的任何已知力。这两个矩阵中给出。最后一项代表类似噪声动态模型的随机扰动。噪声被认为是零均值高斯白噪声。

与输入连续时间系统噪声通过线性随机微分方程描述。与输入离散时间系统噪声通过线性随机微分方程描述。甲状态空间是一个物理系统，其中的输入，输出，和状态变量由一阶耦合方程相关的数学模型。

测量模型

测量是你对你的系统的观察。测量依赖于状态向量，但并不总是与状态向量相同。例如，在雷达系统中，测量可以是球坐标，如距离、方位角和仰角，而状态向量是笛卡尔坐标的位置和速度。对于线性卡尔曼滤波器，测量值总是状态向量的线性函数，排除了球坐标。若要使用球坐标，请使用扩展卡尔曼滤波器。

该测量模型假设任意时刻的实际测量值与当前状态有关

ž ķ = H ķ X ķ + w ^ ķ

w ^ķ表示在当前时间步骤测量噪声。测量噪声也是零均值高斯白噪声协方差矩阵Q通过描述Qķ= E [nķñķŤ]。

线性卡尔曼滤波方程

在无噪声的情况下，动态方程为

X ķ + 1 = F ķ X ķ + G ķ ü ķ 。

同样，测量模型对测量噪声没有贡献。在每个实例中，过程和测量噪声都是未知的。只有噪声统计是已知的。的

ž ķ = H ķ X ķ

你可以把这些方程放到一个递归循环中来估计状态是如何变化的，以及状态分量的不确定性是如何变化的。

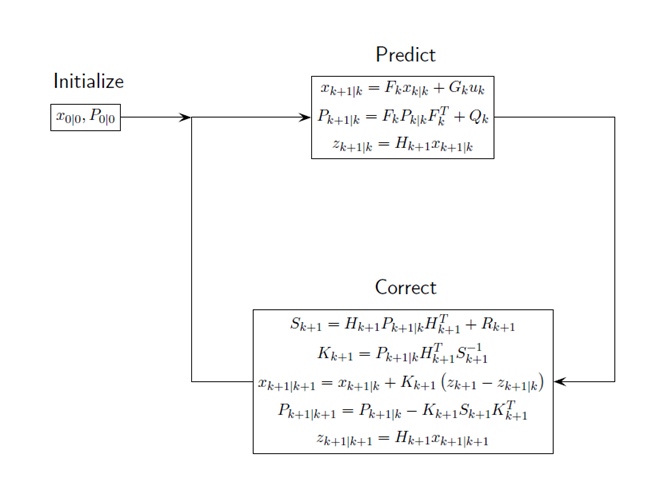
滤波回路

从对这个州的最佳估计开始，X0/0，状态协方差，P0/0。该滤波器执行在连续循环这些步骤。

  1. 传播的状态使用运动方程下一步骤。

    X ķ + 1 | ķ = F ķ X ķ | ķ + G ķ ü ķ 。

    同样传播协方差矩阵。

    P ķ + 1 | ķ = F ķ P ķ | ķ F ķ Ť + Q ķ 。

    下标符号k + 1 | k表示该量是最佳的估计在k + 1从步骤步骤传播ķ。这种估计通常被称为先天的估计。

    然后在更新的时间预测测量。

    ž ķ + 1 | ķ = H ķ + 1 X ķ + 1 | ķ

  2. 利用实际测量值与预测测量值的差值，在更新时对状态进行修正。校正需要计算卡尔曼增益。要做到这一点，首先要计算测量预测协方差(创新)

    小号 ķ + 1 = H ķ + 1 P ķ + 1 | ķ H ķ + 1 Ť + [R ķ + 1

    那么卡曼增益是

    ķ ķ + 1 = P ķ + 1 | ķ H ķ + 1 Ť 小号 ķ + 1 - 1

    和是由使用最优条件得到的。

  3. 校正与测量预测的估计。假设估计是所预测的状态和测量的线性组合。修正后使用下标符号的估计，k + 1 | k + 1。从计算

    X ķ + 1 | ķ + 1 = X ķ + 1 | ķ + ķ ķ + 1 （ ž ķ + 1 - ž ķ + 1 | ķ ）

    哪里ķk + 1是卡尔曼增益。正确的状态通常称为后验状态的估计，因为它是在测量之后得到的。

    修正状态协方差矩阵

    P ķ + 1 | ķ + 1 = P ķ + 1 | ķ - ķ ķ + 1 小号 ķ + 1 ķ “ ķ + 1

    最后，你可以计算基于修正状态的测量。这不是一个校正测量，但什么样的测量将基于状态的最佳估计数进行最佳估计。这相较于实际测量为您提供了过滤器的性能的指示。

此图总结了卡尔曼循环操作。

恒速模型

线性卡尔曼滤波器包含一个内置的线性等速运动模型。可替换地，可以指定为线性运动的转换矩阵。在下一时间步骤中的状态更新为状态的在当前时间的线性函数。在这种过滤器中，测量也由测量矩阵中描述的状态的线性函数。为对象在3-d空间中移动，该状态是由位置和速度在所描述的X- - - - - -,ÿ- 和ž坐标。恒速运动的状态转换模型为

[ X ķ + 1 v X ， ķ + 1 ÿ ķ + 1 v ÿ ， ķ + 1 ž ķ + 1 v ž ， ķ + 1 ] = [ 1 Ť 0 0 0 0 0 1 0 0 0 0 0 0 1 Ť 0 0 0 0 0 1 0 0 0 0 0 0 1 Ť 0 0 0 0 0 1 ] [ X ķ v X ， ķ ÿ ķ v ÿ ， ķ ž ķ v ž ， ķ ]

测量模型是状态向量的一个线性函数。最简单的情况是其中的测量是状态的位置的部件。

[ 米 X ， ķ 米 ÿ ， ķ 米 ž ， ķ ] = [ 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 ] [ X ķ v X ， ķ ÿ ķ v ÿ ， ķ ž ķ v ž ， ķ ]

恒加速模型

线性卡尔曼滤波器包含一个内置的线性恒定加速度运动模型。或者，您可以为恒定加速度的线性运动指定转换矩阵。线性加速度的过渡模型为

[ X ķ + 1 v X ， ķ + 1 一个 X ， ķ + 1 ÿ ķ + 1 v ÿ ， ķ + 1 一个 ÿ ， ķ + 1 ž ķ + 1 v ž ， ķ + 1 一个 ž ， ķ + 1 ] = [ 1 Ť 1 2 Ť 2 0 0 0 0 0 0 0 1 Ť 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 Ť 1 2 Ť 2 0 0 0 0 0 0 0 1 Ť 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 Ť 1 2 Ť 2 0 0 0 0 0 0 0 1 Ť 0 0 0 0 0 0 0 0 1 ] [ X ķ v X ， ķ 一个 X ， ķ ÿ ķ v ÿ ， ķ 一个 ÿ ， ķ ž ķ v ž ， ķ 一个 ž ， ķ ]

最简单的情况是其中的测量是状态的位置的部件。

[ 米 X ， ķ 米 ÿ ， ķ 米 ž ， ķ ] = [ 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 ] [ X ķ v X ， ķ 一个 X ， ķ ÿ ķ v ÿ ， ķ 一个 ÿ ， ķ ž ķ v ž ， ķ 一个 ÿ ， ķ ]

也可以看看

对象

传感器融合和跟踪工具箱文件
万博1manbetx

尝试MATLAB，Sim万博1manbetxulink和其他产品s manbetx 845

得到审判现在