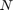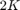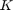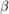建立Watts-Strogatz小世界图模型
此示例演示如何构造和分析Watts Strogatz小世界图。Watts-Strogatz模型是一个随机图，具有小世界网络特性，例如集群和短平均路径长度。
算法描述
创建Watts Strogatz图有两个基本步骤：
使用创建环形晶格
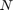平均度节点
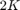。每个节点都连接到其
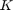两边距离最近的邻居。对于图中的每条边，用概率重新连接目标节点
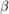.重新布线的边缘不能是重复或自循环。
在第一步之后，图是一个完美的环格。那么什么时候呢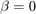
，没有边重新布线，模型返回环形晶格。相反，当
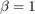，将所有边重新布线，并将环形晶格转换为随机图。
档案瓦特斯特罗加茨为无向图实现此图算法。输入参数为N,K,β根据上述算法描述。
查看文件瓦特斯特罗加茨．
版权所有2015 The MathWorks, Inc.函数h=瓦特斯特罗加茨（N，K，β）%H=WattsStrogatz（N，K，beta）返回一个带有N的Watts Strogatz模型图%节点，N*K条边，平均节点度2*K，重新布线概率beta。%% = 0是一个环格，而= 1是一个随机图。%连接每个节点到它的下一个和前一个邻居K。这个结构%环格的指数。s = repelem ((1: N), 1, K);t = s + repmat(1:K,N,1);t =国防部(t - 1 N) + 1;用概率重新连接每条边的目标节点对于source=1:N switchEdge = rand(K, 1) < beta;newTargets = rand(N, 1);newTargets(源)= 0;newTargets (s (t = =)) = 0;newTargets(t(source， ~switchEdge)) = 0;[~， ind] = sort(newTargets，“下降”)t（信源、开关边缘）=ind（1:nnz（开关边缘））；终止h =图(s, t);终止
环晶格
使用WattsStrogatz函数。当β为0时，该函数返回一个其节点都具有度的环形晶格2K．
h=瓦特斯特罗加茨（500,25,0）；曲线图（h，“NodeColor”,“k”,“布局”,“圆圈”）;头衔(“具有$N=500$、K=25$和$\beta=0$节点的Watts Strogatz图”,...“翻译”,“乳胶”)
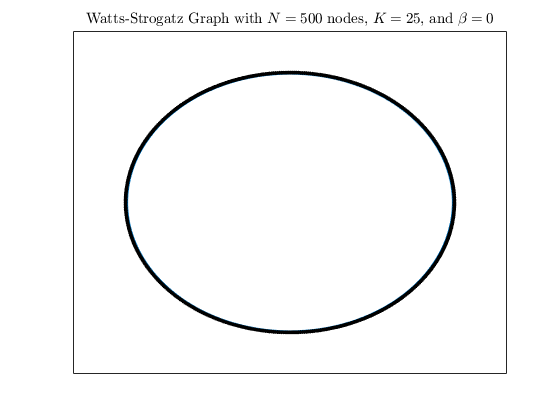
一些随机的边缘
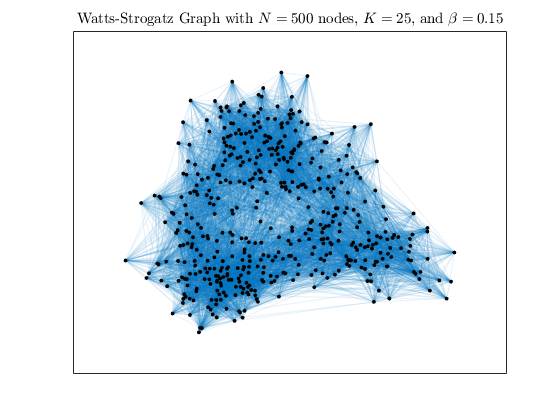
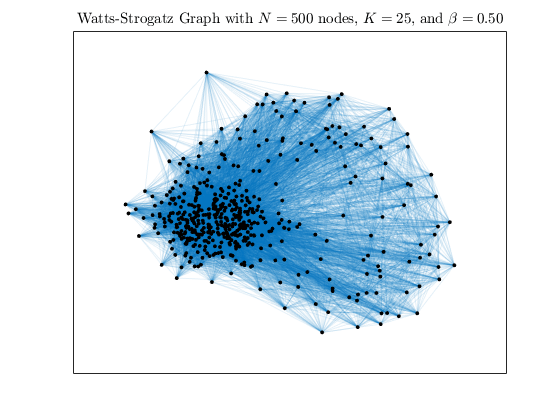
通过提升来增加图表中的随机性数量β到0.15和0.50．
h2 = WattsStrogatz(500年,25岁,0.15);情节(h2,“NodeColor”,“k”,“EdgeAlpha”，0.1）；标题('Watts-Strogatz Graph with $N = 500$ nodes， $K = 25$， and $\beta = 0.15$',...“翻译”,“乳胶”)
h3=瓦特斯特罗加茨（500,25,0.50）；曲线图（h3，“NodeColor”,“k”,“EdgeAlpha”，0.1）；标题(“具有$N=500$、K=25$和$\beta=0.50$节点的Watts Strogatz图”,...“翻译”,“乳胶”)
随机图
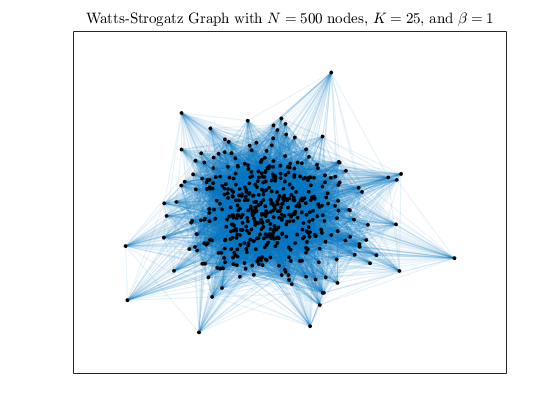
通过递增生成一个完全随机的图β最大值1．0．这重新布线了所有的边。
h4 = WattsStrogatz(1) 500年,25日;情节(h4,“NodeColor”,“k”,“EdgeAlpha”，0.1）；标题(“具有$N=500$、K=25$和$\beta=1$节点的Watts Strogatz图”,...“翻译”,“乳胶”)
度分布
在不同的Watts-Strogatz图中，节点的度分布是不同的。当β为0时，所有节点的度数相同，2K，所以度分布只是一个以2K,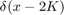
.然而β增加，度分布改变。
此图显示了非零值的度分布β．
直方图（度数（h2），“BinMethod”,“整数”,“FaceAlpha”, 0.9);持有在直方图（度数（h3），“BinMethod”,“整数”,“FaceAlpha”，0.9）；直方图（度数（h4），“BinMethod”,“整数”,“FaceAlpha”，0.8）；保持从头衔(“Watts-Strogatz模型图的节点度分布”)包含(“节点度”) ylabel (节点的数量)传奇(“\beta=1.0”,“\beta=0.50”,“\beta=0.15”,“位置”,“西北”)
枢纽形成
Watts-Strogatz图具有较高的聚类系数，因此节点倾向于形成团，或紧密连接的节点的小群体β向其最大值增加1．0，您会看到越来越多的中心节点，或相对度较高的节点。中心是图中其他节点之间和派系之间的常见连接。中心的存在允许在保持较短平均路径长度的同时形成派系。
计算每个值的平均路径长度和中心节点数β.在本示例中，中心节点是阶数大于或等于55的节点。这些节点是阶数比原始环形晶格增加10%或更多的所有节点。
n = 55;D = [mean(mean(distance (h)))， nnz(degree(h))>=n);...平均(平均(距离(h2))), nnz(学位(h2) > = n);...平均值（平均距离（h3）），nnz（度数（h3）>=n；平均值（平均距离（h4）），nnz（度数（h4）>=n）]；T=表（[0.15 0.50 1]），d（：，1），d（：，2），...“变化无常”，{“贝塔”,“AvgPathLength”,“NumberOfHubs”}）
T=4x3表Beta平均路径长度轮毂数uuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuuu0.15 20.5 1.9101 85 1.9008 92
像β增加时，图中的平均路径长度迅速下降到其极限值。这是由于形成了高度连接的枢纽节点，这些节点变得越来越多β增加。
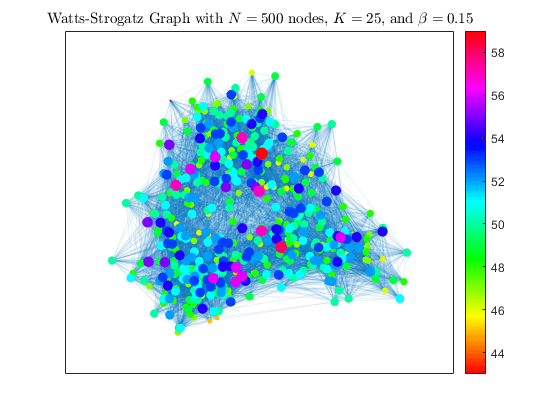
画出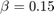
Watts-Strogatz模型图，使每个节点的大小和颜色与其程度成比例。这是可视化枢纽形成的一种有效方法。
colormap高速列车度=学位(h2);nSizes = 2 *√(deg-min(度)+ 0.2);nColors =度;情节(h2,“MarkerSize”nSizes,“NodeCData”，nColors，“EdgeAlpha”，0.1）标题('Watts-Strogatz Graph with $N = 500$ nodes， $K = 25$， and $\beta = 0.15$',...“翻译”,“乳胶”) colorbar
另见
你也可以从以下列表中选择一个网站:
