直角坐标- MATLAB和Simulink万博1manbetx - 万博1manbetx,s manbetx 845,万博尤文图斯

直角坐标系中

坐标的定义

通过指定三个相互正交的坐标轴，为三维空间构造一个直角坐标系或笛卡尔坐标系。下图显示了坐标轴的一种可能规格。

直角坐标将给定坐标系中的空间位置指定为有序的实数三元组，(x，y，z)，相对于原点(0,0,0)。中讨论了选择原点的注意事项全球和本地坐标系．

你可以把三元组看作空间中的一个点，或者等价地看作三维欧几里得空间中的一个向量。将坐标轴视为向量空间，坐标轴是基向量，向量给出了从原点到空间中一点的方向。空间中的每一个向量都是由基向量的线性组合唯一决定的。三维欧几里得空间中最常见的基向量集合是标准单位基向量:

$｛［ 1 0 0 ］，［ 0 1 0 ］，［ 0 0 1 ］｝$

向量和点的符号

在相控阵系统工具箱™软件中，将坐标轴和点指定为列向量。

请注意

在这个软件中，所有的坐标向量都是列向量。为方便起见，文档以[X y z没有转置符号。

矢量符号[X y z]和点表示法(x，y，z)可以互换使用。将列向量解释为向量或点取决于上下文。如果列向量指定了一个坐标系的轴或方向，它就是一个向量。如果列向量指定坐标，它就是一个点。

正交基与欧氏范数

任何三个线性无关的向量定义了三维空间的一组基。然而，这个软件假设你使用的基向量是正交的。

空间中的标准距离是l²标准，或者欧几里得标准。向量的欧几里得范数[X y z定义为:

$\sqrt{x^{2} + y^{2} + z^{2}}$

欧几里得范数给出了从原点开始测量的向量的长度，作为直角三角形的斜边。两个向量之间的距离[x₀y₀z₀]和[x₁y₁z₁)是:

$\sqrt{{（ x_{0} - x_{1} ）}^{2} + {（ y_{0} - y_{1} ）}^{2} + {（ z_{0} - z_{1} ）}^{2}}$

坐标轴方向

给定表示坐标轴的基向量的标准正交集合，有多种方法来定位坐标轴。下图说明了一个这样的方向，称为a右撇子坐标系统。坐标轴上的箭头表示正方向。

如果你用右手沿着正极指向x-轴，手掌朝正y-轴并伸出拇指，拇指指向正方向z设在。

旋转和旋转矩阵

在三维空间中变换向量时，经常遇到旋转矩阵。旋转矩阵的使用有两种意义:它们可以用于将一个向量旋转到一个新的位置，也可以用于将一个坐标基(或坐标系)旋转到一个新的位置。在这种情况下，向量是单独的，但它在新基中的分量将不同于原始基中的分量。在欧几里得空间中，有三种基本的旋转:分别围绕x、y和z轴旋转。每一次旋转都由一个旋转角度指定。当观察者沿旋转轴向原点看时，旋转角度被定义为逆时针旋转的正角。任何任意旋转都可以由这三种旋转组合而成(欧拉旋转定理)．例如，你可以在任意方向上旋转一个向量，使用三个旋转序列: $v^{”} ＝一个 v ＝ R_{z} （ γ ） R_{y} （ β ） R_{x} （ α ） v$ ．

围绕x、y和z轴旋转向量的旋转矩阵由:

绕x轴逆时针旋转

$R_{x} （ α ）＝［ \begin{matrix} 1 & 0 & 0 \\ 0 & 因为 α & - 罪 α \\ 0 & 罪 α & 因为 α \end{matrix} ］$
绕y轴逆时针旋转

$R_{y} （ β ）＝［ \begin{matrix} 因为 β & 0 & 罪 β \\ 0 & 1 & 0 \\ - 罪 β & 0 & 因为 β \end{matrix} ］$
绕z轴逆时针旋转

$R_{z} （ γ ）＝［ \begin{matrix} 因为 γ & - 罪 γ & 0 \\ 罪 γ & 因为 γ & 0 \\ 0 & 0 & 1 \end{matrix} ］$

下面三张图显示了每个旋转轴的正旋转情况:

对于任何旋转，都有一个令人满意的反向旋转 ${一个}^{- 1} 一个＝ 1$ ．例如，通过改变角度的符号，可以得到x轴旋转矩阵的逆:

$R_{x}^{- 1} （ α ）＝ R_{x} （ - α ）＝［ \begin{matrix} 1 & 0 & 0 \\ 0 & 因为 α & 罪 α \\ 0 & - 罪 α & 因为 α \end{matrix} ］＝ R_{x}^{”} （ α ）$

这个例子说明了一个基本性质:逆旋转矩阵是原矩阵的转置。旋转矩阵满足A 'a = 1，因此det(A) = 1．在旋转下，矢量的长度和矢量之间的夹角都被保留。

我们可以用另一种方式来考虑旋转。考虑原始的基向量集合， $我， j ， k$ ，并使用旋转矩阵将它们全部旋转一个．这就产生了一组新的基向量 $我^{”} ， j ，^{”} k^{”}$ 与原文有关的由:

$\begin{array}{l} 我^{”} & ＝一个我 \\ j^{”} & ＝一个 j \\ k^{”} & ＝一个 k \end{array}$

使用转置，你可以把新的基向量写成旧基向量的线性组合:

$［ \begin{matrix} 我^{”} \\ j^{”} \\ k^{”} \end{matrix} ］＝ {一个}^{”} ［ \begin{matrix} 我 \\ j \\ k \end{matrix} ］$

现在任何向量都可以写成任意一组基向量的线性组合:

$v ＝ v_{x} 我 + v_{y} j + v_{z} k ＝ {v^{”}}_{x} 我^{”} + {v^{”}}_{y} j^{”} + {v^{”}}_{z} k^{”}$

使用代数操作，当基(或坐标系)旋转时，您可以导出固定向量的分量变换。这个变换使用旋转矩阵的转置。

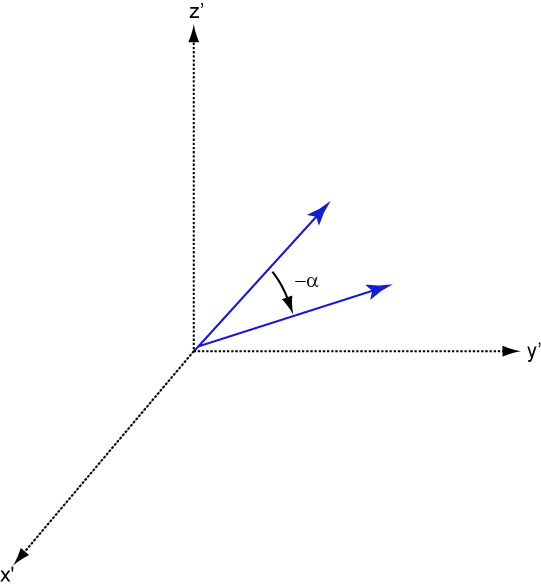
$［ \begin{matrix} {v^{”}}_{x} \\ {v^{”}}_{y} \\ {v^{”}}_{z} \end{matrix} ］＝ {一个}^{- 1} ［ \begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix} ］＝ {一个}^{”} ［ \begin{matrix} v_{x} \\ v_{y} \\ v_{z} \end{matrix} ］$

下一张图说明了当坐标系围绕x轴旋转时矢量是如何转换的。下图显示了如何将这个变换解释为旋转向量的相反的方向。