张量积样条的近似
因为工具箱可以处理样条向量系数,很容易实现插值或近似网格数据张量积样条,如下图所示。你也可以运行例子“二元张量积样条”。
可以肯定的是,大多数张量积样条逼近网格数据可以直接通过样条构造命令之一获得,例如spapi或csape,不需要考虑本示例中讨论的细节。相反,这个例子是为了说明张量积构造背后的理论,这将在本工具箱中的构造命令没有涵盖的情况下有所帮助。
本节讨论了张量产品样条问题的这些方面:
地点和结的选择
考虑,例如,对给定数据的最小二乘近似z(我,j) =f(x(我),y(j)),我= 1:Nx,j= 1:纽约.您从广泛使用的函数中获取数据(见R. Franke,“对分散数据插值的一些方法的关键比较”,海军研究生院技术。众议员nps - 53 - 79 - 003, 1979年3月)。它的定义域是单位平方。您选择了更多的数据站点x方向比y方向;此外,为了更好的定义,您可以在边界附近使用更高的数据密度。
x =([(0:10) / 10。0.07, 0.93 .97]);y =(((0:6) / 6,。0.07, 0.93 .97]);[xx, yy] = ndgrid (x, y);z =因特网(xx和yy);
最小二乘作为y的功能
把这些数据当作来自向量值函数,即y其价值在y(j)为向量z(:,j),所有j.没有特别原因,选择通过矢量值近似函数抛物线样条,有三个等间距内节.这意味着您选择样条的顺序和这个向量值样条的结序列为
肯塔基州= 3;knotsy = augknt([0二十五分。5。1),肯塔基州);
sp = spap2 (knotsy,肯塔基州,y, z);
实际上,你会同时发现离散最小二乘逼近年代肯塔基州,knotsy给每一位Nx数据集
特别是这些表述
yy =约:.05:1.1;瓦尔斯= fnval (sp、yy);
提供一个数组瓦尔斯的条目瓦尔斯(i, j)可以被视为价值的近似值f(x(我),yy.(j))潜在的功能f在网格点x(我),yy.(j),因为瓦尔斯(:,j)是价值yy.(j)近似样条曲线sp.
这一点在命令获得的下图中很明显:
网格(x, yy,瓦尔。”),视图(150年,50)
注意瓦尔斯。”,在网命令,因为MATLAB需要®绘制数组时的面向矩阵视图。这在二元近似中可能是一个严重的问题,因为习惯上是这样想的z(我,j)作为点的函数值(x(我),y(j),而MATLAB则认为z(我,j)作为点的函数值(x(j),y(我))。
假装成曲面的平滑曲线家族
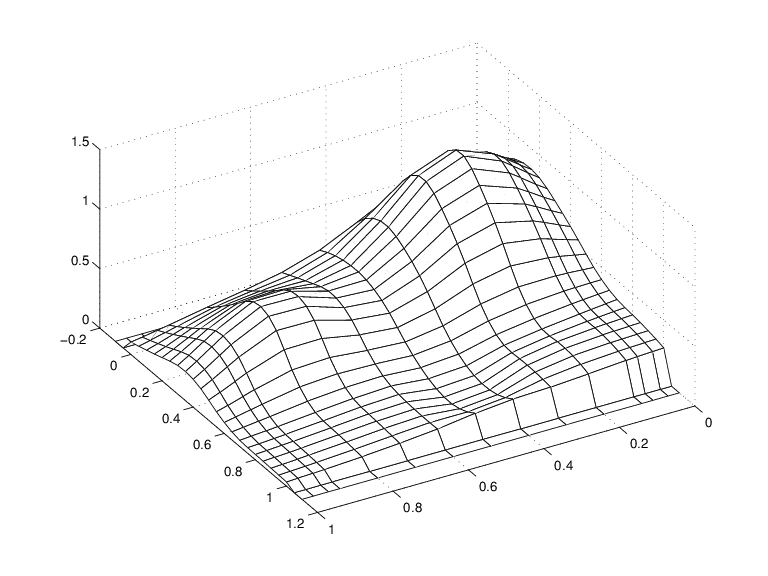
注意,每个平滑曲线上的前两个和后两个值实际上都是零,因为前两个和后两个站点都在yy.超出了样条的基本间隔sp.
还要注意脊。它们证实你只在一个方向上绘制平滑的曲线。
近似与系数作为x的函数
为了得到一个真实的表面,你现在需要更进一步。看看这些系数coefsy样条的sp:
cofsy = fnbrk(sp,'cofs');
抽象地,你可以想到样条曲sp作为功能
与我th条目cofsy(我,r)向量系数coefsy (:, r)对应于x(我),为所有我.这表明近似每个系数矢量coefsy (q,:)用同样顺序的样条kx并且具有相同的合适结序列knotsx.没有特别的原因,这次使用立方样条函数与四个均匀分布的内部结点:
kx = 4;knotsx =奥克纳特([0:.2:1],kx);sp2 = spap2(knotsx,kx,x,cofsy。');
请注意,spap2(节,k, x,外汇)预计外汇(:,J.)作为基准x(j),即期望每一个列的外汇函数值。以符合基准coefsy (q,:)在x(问),为所有问、现在spap2与转置的coefsy.
二元近似
现在考虑系数的转置cxy得到的样条曲线:
系数= fnbrk (sp2,“系数”)。”;
它提供了二元样条逼近
到原始数据
在网格(例如,网格)上绘制此样条曲面
十五= 0:.025:1;青年志愿= 0:.025:1;
你可以做以下事情:
Franke函数的样条逼近
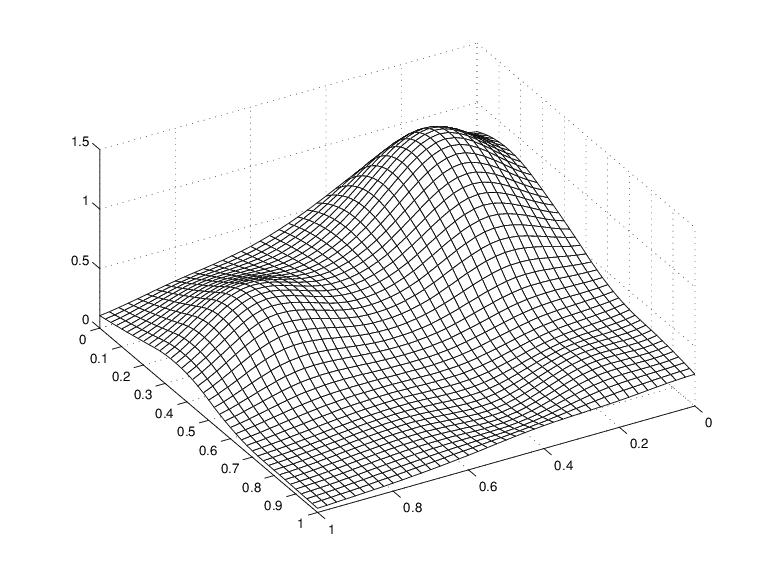
这很有道理,因为spcol (knotsx kx,十五)是其(我,问)第th项等于值B问,kx(十五(我))十五(我)的问b样条的顺序kx对于结序列knotsx.
因为矩阵spcol (knotsx kx,十五)和spcol (knotsy、肯塔基州、青年志愿)是带状的,它可能更有效率,尽管可能更消耗内存大十五和yv.利用fnval,如下所示:
value2 =…fnval (spmak (knotsx fnval (spmak (knotsy系数),青年志愿)。“),十五)。”;
事实上,当fnval用张量积样条直接调用,比如
value2 = fnval (spmak ({knotsx, knotsy},系数),{十五,青年志愿});
以下是相对误差的计算,即给定数据与这些数据地点的近似值与给定数据大小之间的差值:
误差= z - spcol(knotsx,kx,x)* cofs * spcol(Knotsy,Ky,Y)。';disp(max(max(abs(abs(abs)))/ max(max(abs(z))))))
输出是0.0539,也许不太令人印象深刻。但是,系数阵列仅为尺寸8 6
disp(大小(系数)
以适应大小的数据数组15 11..
disp(大小(z))
按顺序切换
这里采用的方法似乎是有偏见的,用下面的方法。首先考虑给定的数据z的向量值函数y,然后处理由近似曲线的矢量系数形成的矩阵,如描述矢量值函数x.
如果你用相反的顺序,也就是思考,会发生什么呢z的向量值函数x然后,然后将从近似曲线的矢量系数组成的矩阵,如描述矢量值的函数y?
也许令人惊讶的是,最终的近似是相同的,直到四舍五入。这是一个数值实验。
作为x的功能最小二乘近似
首先,用样条曲线拟合数据,但这次用x作为自变量,因此它是行的z现在成为数据值。相应地,您必须提供z。',而不是z,spap2,
spb = spap2 (knotsx kx, x, z。');
从而获得所有曲线的样条近似(x;z(:,j))。特别是这个表述
十五,valsb = fnval (spb)。';
提供了矩阵valsb.的条目valsb (i, j)可以被视为价值的近似值f(十五(我),y(j))潜在的功能f在网格点(十五(我),y(j))。当你绘制时,这很明显valsb.使用网:
网格(十五,y, valsb。”),视图(150年,50)
另一个普通的曲线假装是表面
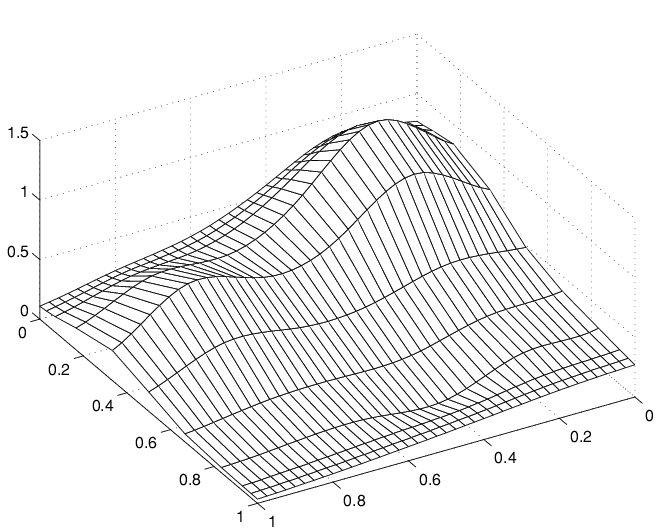
注意山脊。它们证明了,再一次,只在一个方向绘制平滑曲线。但这一次,曲线走向了另一个方向。
近似与系数作为y的函数
现在是第二步,得到实际的表面。首先,提取系数:
“系数”coefsx = fnbrk (spb);
然后适合每个系数矢量coefsx (r,:)用同样顺序的样条肯塔基州并且具有相同的合适结序列knotsy:
注意,再一次,你需要转置系数数组spb,因为spap2将其最后一个输入参数的列作为数据值。
相应地,现在没有必要转换系数阵列coefsb产生的曲线:
coefsb = fnbrk (spb2“系数”);
二元近似
主张是coefsb等于前面的系数数组系数,到四舍五入,下面是测试:
max(max(abs(coefs - coefsb))))
输出是1.4433 e15汽油.
解释很简单:系数c样条的年代包含在sp = spap2(节,k, x, y)依赖线性输入值y.这意味着c和y是一行矩阵吗,是某个矩阵吗一个=一个节,k,x这
对于任何数据y.这个语句甚至适用于wheny是一个矩阵,大小d-经过-N,在这种情况下,每个数据y(:,j)被认为是一个点Rd,得到的样条也相应d-向量值,因此它的系数数组c是尺寸d-经过-n, n =长度(节)- k.
特别是这些表述
sp = spap2 (knotsy,肯塔基州,y, z);coefsy = fnbrk (sp,“系数”);
给我们提供矩阵coefsy满足
随后的计算
sp2 = spap2 (knotsx kx, x, coefsy。');系数= fnbrk (sp2,“系数”)。”;
生成系数数组系数,考虑到两个换位,满足
在第二种,计算中,你首先计算
spb = spap2 (knotsx kx, x, z。');“系数”coefsx = fnbrk (spb);
因此coefsx= z”。一个knotsx, kx, x.随后的计算
spb2 = spap2 (knotsy,肯塔基州,y, coefsx。');“系数”coefsb = fnbrk (spb);
然后提供
因此,coefsb=系数.
比较和扩展
第二种方法比第一种方法更对称,因为在每个调用中都发生了换位spap2无处可去。这种方法可用于近似以任何数量的变量中的网格数据。
例如,如果给定的数据三- 一些三维阵列包含在一些三维阵列中v大小[NX,NY,NZ],v (i, j, k)包含该价值f(x(我),y(j),z(k),然后开始
纽约系数=重塑(v, Nx *新西兰);
假如说nj =结j -kj,对于j =x, y, z,你可以按如下步骤进行:
sp = spap2(knotsx,kx,x,cofs。');Coefs = Rehape(FNBRK(SP,'COEFS'),NY,NZ * NX);sp = spap2(Knotsy,Ky,Y,Cofs。');Coefs = Rehape(FNBRK(SP,'COEFS'),NZ,NX * NY);sp = spap2(knotsz,kz,z,cofs。');Coefs = Rehape(FNBRK(SP,'COEFS'),NX,NY * NZ);
见第17章动力或[C.De Boor,“高效的计算机操纵张量产品”,s manbetx 845ACM反式。数学。软件5(1979),173-182;有关更多细节,Corrigenda,525]相同的参考资料还明确表示使用最小二乘近似没有什么特别的。任何近似过程,包括样条插值,其结果近似具有在给定数据上线性地线性地具有依赖性的系数,可以以与多变量近似过程相同的方式扩展到网格数据。
这正是在样条构造命令中使用的csapi,csape,spapi,spaps,spap2,当网格数据拟合时。它也被用于fnval,当张量积样条在网格上求值时。

