四元数是复数的推广，在计算机图形学和许多其他领域都有应用。

目录

埃德·安吉尔

埃德·安吉尔是我在加州理工学院和新墨西哥州的老朋友流行的一系列教科书关于计算机图形学，现在已经到了第8版。书中介绍了OpenGL编程语言从硅图形到WebGL和JavaScript的演变。Ed正在开发MATLAB版本，我正在kibitzing。

二维

二维生活很简单。平面上的一点很容易用笛卡尔坐标$（x，y）$或极坐标$（r，\theta）来描述$，或单个复数$z$。通过将笛卡尔坐标乘以2×2正交矩阵，或通过增加极角，或通过将$z$乘以另一个复数，可以轻松描述点围绕原点的旋转。

三维

三维的情况更为复杂。有笛卡尔坐标$（x，y，z）$或球坐标$（r，θ，psi）$。但什么是单一复数的三维模拟？旋转更为复杂。它们需要指定旋转轴和角度。还有很多3乘3的正交矩阵，可以选择旋转。

哈密顿

威廉·罗恩·汉密尔顿（1805-1865）他是爱尔兰数学家，都柏林三一学院教授，爱尔兰皇家天文学家。他的名字与整个数学和物理学中的重要概念联系在一起。和他那个时代的许多其他数学家一样，他试图通过添加第二个复数单位来概括二维复数，但没有成功。1846年，他实现了真正意义上的数字他意识到他实际上需要添加三个复杂单元，$i$、$j$和$k$。

点积和叉积s manbetx 845

汉密尔顿四元数算法的关键成分是点积和叉积。点积，也称为内积，是任意维线性代数的常见特征。两个向量的点积是标量。s manbetx 845

$$a\cdot b=a_1 b_1\+\a_2 b_2\+\a_3 b_3$$

叉积仅在三维中定义。两个向量的叉积是第三个向量，方向垂直于前两个向量所跨越的平面。如果$i$、$j$和$k$是三维轴的单位向量，则向量$a$和$b$的叉积为

$$a\times b=（a\u 2 b\u 3-a\u 3 b\u 2）\i\\\（a\u 3 b\u 1-a\u 1 b\u 3）\j\\\（a\u 1 b\u 2-a\u 2 b\u 1）\k$$

下面是交叉产品的快照。

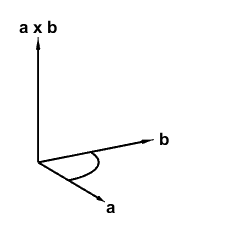
向量垂直于跨越$a$和$b$的平面有两种可能的方向。传统的选择是通过这张瑞士钞票上的右手规则和Facebook公司办公室标志上的表情符号。

四元数

四元数$q$有两部分，标量$s$和向量$v$。标量是一个实数；将$s$视为标量单位的系数，$1$。向量由三个实数组成；它们是三个虚单位的系数，$i$，$j$和$k$。所以

$$q=[s，v]=s1\+\vu 1i\+vu 2j\+\vu 3k$$

四元数乘法的定义使得每个虚单位都是$-1$的平方根。

$$i^2=-1，\\j^2=-1，\\k^2=-1$$

此外，这三个单元通过其乘积的循环性质相互关联。s manbetx 845

$$ij=k，\\jk=i，\\ki=j$$

这些性质意味着

$$ji=-k，\\kj=-i，\\ik=-j$$

让我们把乘法下的$i$、$j$和$k$的这些性质称为“汉密尔顿规则”。

四元数加法

假设我们有两个四元数。

$$p=[r，u]=r 1\+\u_1 i\+u_2 j\+\u_3 k$$

$$q=[s，v]=s1\+\vu 1i\+vu 2j\+\vu 3k$$

添加是显而易见的。

$$p+q=[r+s，u+v]$$

四元数乘法

四元数乘法既巧妙又复杂。

$$pq=（r+u_1i+u_2j+u_3k）（s+v_1i+v_2j+v_3k）$$

每个括号中有四个术语，因此产品中有16个术语。请仔细展开，因为$i$、$j$和$k$不会相互转换。应用汉密尔顿规则，$i^2=-1$、$i j=k$、$j i=-k$等。16个术语可以这样排列。

$$p q=[\r s-（u_1 v_1+u_2 v_2+u_3 v_3）\$$

$$\\\\\r（v_1 i+v_2 j+v_3 k）+s（u_1 i+u_2 j+u_3 k）\+（u_2 v_3-u 3 v_2）i+（u_3 v_1-u 1 v_3）j+（u_1 v_2-u 2 v_1）k\]$$

我们认识两个熟悉的量，点积和叉积。s manbetx 845

$$u\cdot v=u_1 v_1+u_2 v_2+u_3 v_3$$

$$u\times v=（u_2 v_3-u_3 v_2）i+（u_3 v_1-u_1 v_3）j+（u_1 v_2-u_2 v_1）k$$

那么结果呢

$$pq=[rsu-u\cdot v，rv+su+u\times v]$$

这是汉密尔顿对四元数积的定义。

单位$i$、$j$和$k$的标量部分等于0，矢量部分等于[1,0,0]、[0,1,0]和[0,0,1]。将这些单位插入产品定义会产生，例如，

$$i^2=[0-i\cdot i，0+0+i\times i]=-1$$，

$$i j=[0-0,0+0+i\times j]=k$$

和

$$j i=j\times i=-i\times j=-k$$

五车二科学

Capella Science是Patreon YouTube频道。https://www.patreon.com/acapellascience.

2016年，Capella Science制作了一段视频，其中有两位汉密尔顿，一位是非常受欢迎的百老汇音乐剧汉密尔顿，另一位是爱尔兰数学家汉密尔顿。https://www.youtube.com/watch?v=SZXHoWwBcDc. 下面是该视频中一帧的屏幕截图。

qtn

MATLAB的2021a和2021b版本包括四元数对象，该对象在多个导航工具箱之间共享。

Ed和我有自己更基本的目标，qtn.

帮助qtn

四元数的基本构造函数。qtn（a，b，c，d）qtn（a，[v1 v2 v3]）qtn（a）方法加上p+q减去p-quminus-qmtimes p*qmldivide p\qmrdivide p/qmpower q^n inv（q）norm（q）disp（q）函数rot Euler randq qtn_示例：所有角度都以度为单位。此对象未矢量化。qtn文档qtn在帮助浏览器中发布的输出showdemo qtn

最重要的qtn方法是四元数乘积。我认为这段代码很优雅。

数据库类型89:96qtn

89函数r=mtimes（p，q）90%p*q91p=qtn（p）；92q=qtn（q）；93 r.s=p.s*q.s-点（p.v，q.v）；94 r.v=p.s*q.v+q.s*p.v+cross（p.v，q.v）；95r=qtn（r）；96完

整个qtn类定义只有大约150行长。

基本的

下面是一些基本四元数对象的示例和测试。

两个单位。

i=qtn（0，[100]）j=qtn（0，[0110]）

i=0+1i+0j+0k j=0+0i+1j+0k

他们的产品是第三单元。

k=i*j

k=0+0i+0j+1k

这三个都是-1。

ijk=i*j*k isq=i^2 ii=i*i

ijk=-1+0i+0j+0k isq=-1+0i+0j+0k ii=-1+0i+0j+0k

随机的

两个随机的qtn具有整数系数的

p=randq=randq

p=2+8i-1j+4k q=0+4i-6j+7k

附加

p_+q=p+q

p_加_q=2+12i-7j+11k

乘法。

pq=p*q

pq=-66+25i-52j-30k

右派。

r=pq/p

r=0+9.6i+2j-2.2k

左师。p \（p*q/p）*p应在舍入误差范围内Q.

test1=norm（p\r*p-q）

测试1=4.4409e-16

轮换

类型腐烂

函数r=rot（θ，v）%rot r=rot（θ，v）是角θ围绕轴v旋转%的四元数（qtn）。v=v/范数（v）；r=qtn（cosd（θ），sind（θ）*v）；结束

一个随机的旋转轴。

v=randn（1,3）

v=-0.12411.4897 1.4090

旋转36度左右v

r=rot（36，v）

r=0.809017-0.0355214i+0.426247j+0.403167k

重复36度旋转10次是360度旋转，应该在四元数乘法恒等式的舍入误差范围内。

e=qtn（1）test2=norm（r^10-e）

e=1+0i+0j+0k测试2=4.6059e-16

密码

（添加，2021年9月11日）。您可以获取qtn以及这些链接中的相关功能：qtn.m,rot.m,欧拉,randq.m,qtn_示例_1.m.

获取MATLAB代码

与MATLAB®R2021b一起发布