代理优化算法
电视连续剧surrogateopt算法
电视连续剧surrogateopt算法概述
代理优化算法在两个阶段之间交替进行。
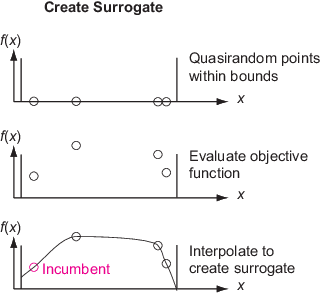
构造代理-创造
选项。MinSurrogatePoints边界内的随机点。在这些点评估(昂贵的)目标函数。通过插值a来构造目标函数的代理函数径向基函数通过这些点。寻找最小-通过在界限内的数千个随机点的抽样来寻找目标函数的最小值。基于这些点的代理值以及它们与(昂贵的)目标函数已被评估的点之间的距离来评估一个价值函数。根据价值函数选择最佳点作为候选点。在最佳候选点评估目标函数。这个点叫做an自适应点. 使用此值更新代理项并再次搜索。
在构造代理阶段,该算法从拟随机序列构造样本点。构造插值径向基函数至少需要nvars+1个采样点,其中nvars是问题变量的数量。的默认值选项。MinSurrogatePoints是据nvar 2 *或20,以较大者为准。
当所有搜索点都太接近(小于选项)时,算法停止搜索最小阶段MinSampleDistance)到目标函数先前计算过的点。看到搜索最低限度的详细信息.这个从搜索最小阶段的开关被调用代理重置.
代理优化的定义
代理优化算法描述使用以下定义。
当前-目标函数最近被评估的点。
在任点-自最近的替代重置以来所有评估的目标函数值最小的点。
最佳-迄今为止所有评估中目标函数值最小的点。
初始化-如果有的话,你传递给解算器的点
初始点选择。随机点-解算器评估目标函数的构造代理阶段中的点。通常,解算器从拟随机序列中获取这些点,缩放并移动以保持在边界内。拟随机序列类似于伪随机序列,如
兰德返回,但间隔更均匀。看见https://en.wikipedia.org/wiki/Low-discrepancy_sequence.然而,当变量数量超过500时,解算器从拉丁超立方序列中取点。看到https://en.wikipedia.org/wiki/Latin_hypercube_sampling.自适应点-搜索解算器评估目标函数的最小阶段中的点。
价值函数-见价值函数定义.
评估点-目标函数值已知的所有点。这些点包括初始点、构造代理点和搜索解算器评估目标函数的最小点。
样本点。解算器在搜索最小阶段期间评估价值函数的伪随机点。这些点不是解算器评估目标函数的点,除非中描述搜索最低限度的详细信息.
构建代理细节
为了构造代理,算法在边界内选择拟随机点。如果你传递一组初始点初始点选项,算法使用这些点和新的拟随机点(如有必要)来达到总数选项。MinSurrogatePoints.
注
如果某些上界和下界相等,surrogateopt在构造代理项之前,从问题中删除这些“固定”变量。surrogateopt无缝管理变量。例如,如果你传递初始点,传递整个集合,包括任何固定变量。
在随后的构造代理阶段,该算法使用选项。MinSurrogatePointsquasirandom点。算法在这些点计算目标函数。
该算法构造一个代理作为目标函数的插值径向基函数(RBF)插入器。RBF插值有几个方便的特性,使它适合于构造代理:
该算法在第一个构造代理阶段仅使用初始点和随机点,在随后的构造代理阶段仅使用随机点。特别是,该算法不使用该代理中搜索最小阶段的任何自适应点。
搜索最低限度的详细信息
解算器通过遵循与局部搜索相关的过程来搜索目标函数的最小值。解算器初始化规模用于值为0.2的搜索。比例类似于模式搜索中的搜索区域半径或网格大小。解算器从当前点开始,该点是自上次代理重置以来目标函数值最小的点。解算器搜索最小值优值函数这与代理和与现有搜索点的距离都有关,以试图平衡最小化代理和搜索空间。看到价值函数定义.
解算器将数百或数千个具有缩放长度的伪随机向量添加到当前点以获得采样点.这些向量都是正态分布,根据每个维度的边界平移和缩放,然后乘以尺度。如果有必要,解算器会改变样本点,使它们保持在界限内。求解器在采样点处计算价值函数,但不在采样点内的任何点处计算options.MinSampleDistance指先前评估的点。具有最低价值函数值的点称为自适应点。解算器评估自适应点处的目标函数值,并使用该值更新代理项。如果自适应点处的目标函数值充分低于当前值,则解算器认为搜索成功,并将自适应点设置为当前点。否则,解算器将认为搜索失败,并且不会更改当前点。

当满足上述第一个条件时,求解器将改变比例:
自上次比例更改以来,已进行了三次成功的搜索。在这种情况下,刻度加倍,最大刻度长度为
0.8乘以边界指定的框的大小。最大值(5,nvar)搜索失败发生在上次尺度变化之后,其中据nvar为问题变量的数量。在这种情况下,刻度被减半,降至最小刻度长度1 e-5乘以边界指定的框的大小。
这样,随机搜索最终集中在目标函数值较小的当前点附近。然后,解算器以几何方式将比例缩小到最小比例长度。
解算器不会在内的点处计算价值函数options.MinSampleDistance求值点(见代理优化的定义)。当所有采样点都在范围内时,解算器将从搜索最小阶段切换到构造代理阶段(换句话说,执行代理重置)MinSampleDistance评估点。一般来说,这个重置发生在求解器缩小规模,以便所有的样本点紧密地聚集在在位点周围之后。
价值函数定义
价值函数f优点(x)是两个词的加权组合:
缩放代理。定义闵作为采样点中的最小代理项值,马克斯作为最大值,并且(x)作为该点的代理值x.然后是缩放代理(x)是
(x)是非负的,并且在各点处为零x在采样点之间具有最小代理项值的。
缩放距离。定义xj,j= 1,…,k作为k评估点。定义dij为到采样点的距离我到评估点k.集d闵=分钟(dij),d马克斯= max (dij),其中最小值和最大值接管所有我和j. 比例距离D(x)是
哪里d(x)为点的最小距离x到一个评估点。D(x)是非负的,并且在各点处为零x最大程度上远离评估点。所以,最小化D(x)将算法引导到远离评估点的点。
价值函数是标度代理项和标度距离的凸组合。对于一个重量w与0<w<1时,价值函数为
很大的价值w强调代理值的重要性,从而使搜索最小化代理值。小值w重视远离评估点的点,从而将搜索引向新区域。在搜索最小值阶段,权重w按照Regis和Shoemaker的建议,循环使用这四个值[2]:0.3、0.5、0.8和0.95。
混合整数surrogateopt算法
混合整数surrogateopt概述
当部分或所有变量为整数时,如intcon参数,surrogateopt改变某些方面的串行代理选择算法.此描述主要是关于变化,而不是整个算法。
算法开始
如有需要,,surrogateopt移动指定的边界intcon点,以便它们是整数。同时,surrogateopt确保提供的初始点是整数可行且相对于边界可行。然后算法生成准随机点,就像在非整数算法中一样,将整数点舍入为整数值。该算法生成的代理与非整数算法完全相同。
整数查找最小值
使用与之前相同的价值函数和权重序列搜索最小值。区别在于surrogateopt使用三种不同的随机点采样方法来定位价值函数的最小值。surrogateopt根据下表选择与权值相关联的一个周期内的采样器。
取样器循环
| 重量 | 0.3 | 0.5 | 0.8 | 0.95 |
| 采样器 | 随机的 | 随机的 | OrthoMADS | 全球定位系统 |
尺度-每个采样器采样点在在任者周围的一个尺度区域内。整数点有一个比例,从边界宽度的½倍开始,并与非整数点精确地调整,除非如果它低于1,宽度将增加到1。连续点的规模发展与非整数算法完全相同。
随机-采样器在一个标度内均匀随机地生成整数点,以当前点为中心。该采样器根据高斯分布生成连续点,平均值为零。整数点样本的宽度乘以比例,连续点的标准偏差也是如此。
采样器均匀随机地选择一个正交坐标系。然后,算法在现有对象周围创建样本点,将当前比例乘以坐标系统中的每个单位向量进行加减运算。该算法将整数点取整。这将创建2N个样本(除非一些整数点被舍入到当前值),其中N是问题维度的数量。OrthoMADS也比2N个固定方向多使用两个点,一个在[+1,+1,…,+1],另一个在[-1,-1,…,-1],总共2N+2个点。然后采样器重复地将2N + 2步减半,在任职者周围创建越来越精细的点集,同时四舍五入整数值点。当有足够的样本或四舍五入没有产生新的样本时,此过程结束。
GPS -采样器类似于OrthoMADS,只不过GPS使用的是非旋转坐标系,而不是随机选择一组方向。
树搜索
在对价值函数的数百或数千个值进行抽样后,surrogateopt通常选择最小值点,对目标函数求值。然而,在两种情况下,surrogateopt在评估目标之前,执行另一个称为树搜索的搜索:
自上次树搜索(称为案例A)以来,共有2N个步骤。
surrogateopt即将执行一个名为案例B的代理重置。
树搜索的过程如下所示,类似于中的过程intlinprog,如分枝定界.算法通过找到一个整数值,创建一个新问题,这个问题有一个上限,这个上限可以是高的,也可以是低的,然后用这个上限来解决子问题。在求解子问题之后,算法选择一个不同的整数,使其上下以1为界。
情形A:使用缩放的采样半径作为整体边界,并运行多达1000步的搜索。
案例B:使用原始问题边界作为总体边界,并运行多达5000个搜索步骤。
在这种情况下,解决子问题意味着运行铁铬镍铁合金“sqp”算法对连续变量,从给定的整数值开始,搜索局部最小的优值函数。
树搜索可能非常耗时。所以surrogateopt有一个内部时间限制,以避免在此步骤中过多的时间,限制了情况A和情况B步骤的数量。
在树搜索的最后,算法利用树搜索找到的点和前面搜索找到的点的优势,用优点函数来度量最小值。算法在这一点上计算目标函数。整数算法的余数与连续算法完全相同。
surrogateopt具有非线性约束的算法
当问题有非线性约束时,surrogateopt以多种方式修改前面描述的算法。
在初始和每次代理重置后,算法创建目标和非线性约束函数的代理。随后,算法的不同取决于构造代理阶段是否找到任何可行点;当构造代理时,寻找可行点等价于在任点是可行的。
在任者是不可行的——这种情况称为第一阶段,涉及到对可行点的搜索。在遇到可行点前的最小阶段搜索中,
surrogateopt更改优点函数的定义。该算法统计每个点上违反的约束数,并仅考虑违反约束数最少的点。在这些点中,该算法选择最大约束违反最小的点作为最佳(最低价值函数)点。这最好的一点是现任者。随后,直到算法遇到一个可行点,它使用对价值函数的这种修改。什么时候surrogateopt计算一个点,发现它是可行的,可行点成为在位点,算法处于阶段2。在位者是可行的——这种情况称为阶段2,以与标准算法相同的方式进行。为了计算价值函数,该算法忽略了不可行点。
该算法根据混合整数surrogateopt算法进行以下更改。以后据nvar 2 *算法评估目标和非线性约束函数的点,surrogateopt调用铁铬镍铁合金函数最小化代理项,受代理项非线性约束和边界约束,其中边界由当前比例因子缩放。(如果现任者不可行,铁铬镍铁合金忽略目标并尝试找到满足约束的点。)如果问题同时具有整数和非线性约束,则surrogateopt电话树搜索而不是铁铬镍铁合金.
如果问题是一个可行性问题,也就是说它没有目标函数,那么surrogateopt在找到可行点后立即执行代理重置。
平行surrogateopt算法
并行surrogateopt算法与串行算法的不同之处如下:
并行算法维持一个点队列,在这个队列上计算目标函数的值。这个队列比并行工作人员的数量大30%。队列大于worker的数量,以减少因为没有点可用来计算而导致worker空闲的机会。
调度器以FIFO方式从队列中获取点,并在工作线程空闲时异步将其分配给工作线程。
当算法在阶段(Search for Minimum和Construct代孕)之间切换时,正在评估的现有点仍在服务中,队列中的任何其他点都将被刷新(从队列中丢弃)。因此,一般来说,算法为Construct代孕阶段创建的随机点的数量最多
选项。MinSurrogatePoints + PoolSize,在那里PoolSize是并行工人的数量。类似地,在代理重置后,算法仍然具有PoolSize - 1员工正在评估的适应性点。
注
目前,并行代理优化不一定给出可再现的结果,因为并行时序的不可再现性可能导致不同的执行路径。
并行混合整数surrogateopt算法
当在混合整数问题上并行运行时,surrogateopt在主机上执行树搜索过程,而不是在并行辅助进程上。使用最新的代理,surrogateopt在每个worker返回一个自适应点之后搜索代理项的较小值。
如果目标函数不昂贵(耗时),那么这个Tree Search过程可能会成为主机上的瓶颈。相反,如果目标函数很昂贵,那么树搜索过程只需要很小一部分的计算时间,并且不会成为瓶颈。
参考文献
[1] 鲍威尔,M.J.D。1990年《径向基函数近似理论》。W.A.(编辑),数值分析进展,第2卷:小波、细分算法和径向基函数。克莱伦登出版社,1992,第105-210页。
[2] 雷吉斯、R.G.和C.A.鞋匠。代价函数全局优化的随机径向基函数方法。《通知J.计算》2007年第19期,第497-509页。
[3] 王和C.A.鞋匠。基于代理模型和灵敏度分析,提出了一种最小化昂贵黑箱目标函数的通用随机算法框架。v1 arXiv: 1410.6271(2014)。可以在https://arxiv.org/pdf/1410.6271.
[4] 古特曼,H-M。一种用于全局优化的径向基函数方法。《全球优化杂志》,2001年3月19日,第201-227页。