Solve Nonstiff ODEs
This page contains two examples of solving nonstiff ordinary differential equations usingode45。MATLAB® has several solvers for nonstiff ODEs.
ode45ode23ode78ode89ode113
For most nonstiff problems,ode45performs best. However,ode23is recommended for problems that permit a slightly cruder error tolerance or in the presence of moderate stiffness. Likewise,ode113can be more efficient thanode45for problems with more stringent error tolerances or when the ODE function is computationally expensive to evaluate.ode78andode89are high-order solvers that excel with long integrations where accuracy is crucial for stability.
If the nonstiff solvers take a long time to solve the problem or consistently fail the integration, then the problem might bestiff。SeeSolve Stiff ODEsfor more information.
Example: Nonstiff van der Pol Equation
The van der Pol equation is a second order ODE
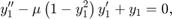
where is a scalar parameter. Rewrite this equation as a system of first-order ODEs by making the substitution
is a scalar parameter. Rewrite this equation as a system of first-order ODEs by making the substitution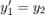 。The resulting system of first-order ODEs is
。The resulting system of first-order ODEs is

The system of ODEs must be coded into a function file that the ODE solver can use. The general functional signature of an ODE function is
dydt = odefun(t,y)
That is, the function must accept bothtandyas inputs, even if it does not usetfor any computations.
函数文件vdp1.mcodes the van der Pol equation using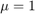 。的变量
。的变量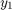 and
and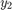 are represented by
are represented byy(1)andy(2), and the two-element column vectordydtcontains the expressions for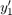 and
and 。
。
functiondydt = vdp1(t,y)%VDP1 Evaluate the van der Pol ODEs for mu = 1%% See also ODE113, ODE23, ODE45.% Jacek Kierzenka and Lawrence F. Shampine% Copyright 1984-2014 The MathWorks, Inc.dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];
Solve the ODE using theode45function on the time interval[0 20]with initial values[2 0]。The output is a column vector of time pointstand a solution arrayy。Each row inycorresponds to a time returned in the corresponding row oft。The first column ofycorresponds to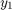 , and the second column to
, and the second column to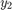 。
。
[t,y] = ode45(@vdp1,[0 20],[2; 0]);
Plot the solutions for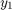 and
and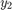 against
againstt。
plot(t,y(:,1),'-o',t,y(:,2),'-o') title('Solution of van der Pol Equation (\mu = 1) using ODE45'); xlabel('Time t'); ylabel('Solution y'); legend('y_1','y_2')

Thevdpodefunction solves the same problem, but it accepts a user-specified value for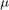 。The van der Pol equations become stiff as
。The van der Pol equations become stiff as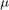 increases. For example, with the value
increases. For example, with the value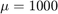 you need to use a stiff solver such as
you need to use a stiff solver such asode15sto solve the system.
Example: Nonstiff Euler Equations
The Euler equations for a rigid body without external forces are a standard test problem for ODE solvers intended for nonstiff problems.
The equations are
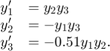
函数文件rigidodedefines and solves this first-order system of equations over the time interval[0 12], using the vector of initial conditions[0; 1; 1]corresponding to the initial values of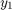 ,
,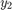 , and
, and 。当地的函数
。当地的函数f(t,y)encodes the system of equations.
rigidodecallsode45with no output arguments, so the solver uses the default output functionodeplotto automatically plot the solution points after each step.
functionrigidode%RIGIDODE Euler equations of a rigid body without external forces.% A standard test problem for non-stiff solvers proposed by Krogh. The% analytical solutions are Jacobian elliptic functions, accessible in% MATLAB. The interval here is about 1.5 periods; it is that for which% solutions are plotted on p. 243 of Shampine and Gordon.%% L. F. Shampine and M. K. Gordon, Computer Solution of Ordinary% Differential Equations, W.H. Freeman & Co., 1975.%% See also ODE45, ODE23, ODE113, FUNCTION_HANDLE.% Mark W. Reichelt and Lawrence F. Shampine, 3-23-94, 4-19-94% Copyright 1984-2014 The MathWorks, Inc.tspan = [0 12]; y0 = [0; 1; 1];% solve the problem using ODE45figure; ode45(@f,tspan,y0);% --------------------------------------------------------------------------functiondydt = f(t,y) dydt = [ y(2)*y(3) -y(1)*y(3) -0.51*y(1)*y(2) ];
Solve the nonstiff Euler equations by calling therigidodefunction.
rigidode title('Solution of Rigid Body w/o External Forces using ODE45') legend('y_1','y_2','y_3','Location','Best')

See Also
ode45|ode23|ode78|ode89|ode113
