主要内容

距离

所有节点对的最短路径距离

折叠所有页面

语法

d =距离(G)
d =距离(G, s)
d =距离(G s t)
d =距离(＿＿＿“方法”,算法)

描述

例子

d=距离(G）返回一个矩阵,d,在那里d (i, j)节点之间最短路径的长度是多少我和节点j．如果图表是加权的(也就是说，G.Edges包含一个变量重量)，然后使用这些权重作为图中沿边的距离。否则，所有的边距离都取为1．

例子

d=距离(G，年代）将源节点限制为年代,这样d (i, j)到节点的距离是多少(我)到节点j．

例子

d=距离(G，年代，t）另外，将目标节点限制为t,这样d (i, j)到节点的距离是多少(我)到节点t (j)．

例子

d=距离(＿＿＿“方法”,算法）可选地指定在使用前面语法中的任何输入参数计算最短路径时使用的算法。例如,如果G是一个加权图吗距离(G,“方法”,“减重”)忽略边的权值G所有边的权值都是1．

例子

全部折叠

打开生活的脚本

创建并绘制图表。

S = [1 1 1 2 5 5 5 8 9];T = [2 3 4 5 6 7 8 9 10];图G = (s, t);情节(G)

图中包含一个坐标轴。坐标轴包含一个graphplot类型的对象。

计算图中所有节点对之间的最短路径距离。由于图的边没有权值，所以取所有边的距离为1。

d =距离(G)
d =600100 1 1 1 2 3 3 3 4 5 1 0 2 2 1 2 2 2 3 4 1 2 0 2 3 4 4 4 5 6 1 2 2 0 3 4 4 4 5 6 2 3 3 0 1 1 1 2 3 3 1 2 4 4 0 2 2 3 4 3 2 4 4 1 2 0 2 3 4 3 2 4 1 2 2 0 1 2 3 4 5 5 4 2 3 3 1 0 5 6 6 3 4 4 2 1 0

d是对称的,因为G是一个无向图。在一般情况下d (i, j)节点之间最短路径的长度是多少我和节点j，对于无向图，这个等价于d (j,我)．

例如，求节点1到节点10之间的最短路径长度。

d (10)
ans = 5
打开生活的脚本

创建并绘制图表。

S = [1 1 1 2 2 3 4 4 5 6];T = [2 3 4 5 3 6 6 5 7 7 7];图G = (s, t);情节(G)

图中包含一个坐标轴。坐标轴包含一个graphplot类型的对象。

找出从节点1、节点2和节点3到图中所有其他节点的最短路径距离。

d =距离(G，[1 2 3])
d =3×70 1 1 1 1 2 2 1 0 1 2 2 1 0 1 2 2 1 1 2 1 1 1 1 1 1 1 2 1 1 2 1 1 1 2 1 1 2 1 1 2 1 2 2 1 2

使用d求节点1到节点7的最短路径距离。

d (7)
ans = 2
打开生活的脚本

创建并绘制图表。

S = [1 11 2 2 3 3 4 5 5 6 7 8 8 10 11];T = [2 3 10 4 12 5 4 6 6 7 9 8 9 11 11 12];图G = (s, t);情节(G)

图中包含一个坐标轴。坐标轴包含一个graphplot类型的对象。

求节点5、7到节点2、3的最短路径距离。

Sources = [5 7];target = [2 3];d =距离(G、来源、目标)
d =2×23 1 4 2

使用d求节点7到节点3之间的最短路径距离。在这种情况下,d (i, j)到节点的距离是多少来源(我)到节点目标(j)．

d (2, 2)
ans = 2
打开生活的脚本

创建并绘制带加权边的有向图。

S = [1 1 1 2 5 3 6 4 7 8 8 8];T = [2 3 4 5 3 6 4 7 2 6 7 5];权重= [100 10 10 10 10 20 10 30 50 10 70 10];G =有向图(s t重量);情节(G,“EdgeLabel”G.Edges.Weight)

图中包含一个坐标轴。坐标轴包含一个graphplot类型的对象。

求所有图节点对之间的最短路径距离。

d =距离(G)
d =8×80 90 10 100 30 40正正0 20 50 10 40 80正正110 0 120 20 60正正80 100 0 90 120 120正正无穷10 40 0 70正正90 110 100 0 40正正50 60 70 100 90 0正正100 20 20 10 10 50 0

自G是一个有向图，d是不对称的，并且d (i, j)对应于节点之间的距离我和j．的正值d对应不可达节点。例如，由于节点1没有前一个节点，因此不可能从图中的任何其他节点到达节点1。所以第一列d包含了许多正值表示节点1不可达。

默认情况下,距离使用边的权值来计算距离。指定“方法”作为“减重”忽略边的权值，将所有边的距离都视为1。

d1 =距离(G,“方法”，“减重”）
d1 =8×80 1 1 1 2 2 2正正0 2 4 1 3 5正正4 0 2 5 1 3正1正2 4 0 3 5正正5 1 3 0 2 4正正3 5 1 4 0 2正正1 3 5 2 4 0正正2 2 2 1 1 1 0

输入参数

全部折叠

输入图形，指定为图或有向图对象。使用图创建无向图或有向图创建有向图。

例子:图G =(1、2)

例子:G =有向图([1,2]，[2 3])

源节点，指定为一个或多个节点索引或节点名，或“所有”选择所有源节点。

该表显示了通过数字节点索引或节点名引用一个或多个节点的不同方法。

形式 单独的节点 多个节点
节点索引

标量

例子:1

向量

例子:(1 2 3)
节点名称

特征向量

例子:“一个”

字符向量的单元格数组

例子:{“A”“B”“C”}

字符串标量

例子:“一个”

字符串数组

例子:(“A”“B”“C”)

年代和t不能指定命名为“所有”或“方法”，因为这些节点名称与选项名称冲突。使用findnode而不是传递这些情况的节点索引。

例子:距离(G, 1 [2])

例子:距离(G,“所有”,[1 3 5])

目标节点，指定为一个或多个节点索引或节点名，或“所有”选择所有目标节点。

年代和t不能指定命名为“所有”或“方法”，因为这些节点名称与选项名称冲突。使用findnode而不是传递这些情况的节点索引。

例子:距离(G, 1 [2])

例子:距离(G,“所有”,[1 3 5])

最短路径算法，指定为表中的选项之一。

选项 描述
“汽车”(默认)

的“汽车”选项自动选择算法:

  • “减重”用于图和有向图没有边权的输入。

  • “积极”用于所有图有边权的输入，并且要求权值是非负的。这个选项也用于有向图具有非负权边的输入。

  • “混合”用于有向图边权值为负值的输入。图不可能有负环。
“减重”

宽度优先计算，将所有边的权值视为1．
“积极”

要求所有边的权值非负的Dijkstra算法。
“混合”(仅供有向图）

有向图的Bellman-Ford算法，它要求图没有负环。

而“混合”是低于“积极”对于同样的问题，“混合”更通用，因为它允许一些边的权值为负。

请注意

对于大多数图形,“减重”是最快的算法，其次是“积极”,“混合”．

例子:距离(G s t,“方法”,“减重”)

输出参数

全部折叠

节点对之间的最短路径距离，以矩阵形式返回。的大小d是(#源节点)by-(#目标节点)。的值正表示路径不存在。

提示

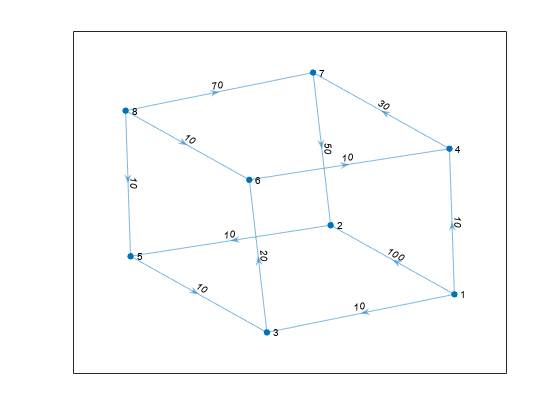
  • 的shortestpath，shortestpathtree,距离函数不支持具有负边权的无向图，或者万博1manbetx更普遍地说，任何包含负环的图，原因如下:

    • 一个消极的循环是一条从节点返回到自身的路径，路径上各边的权值之和为负。如果在两个节点之间的路径上存在一个负环，则节点之间不存在最短路径，因为通过遍历负环总能找到更短的路径。

    • 在无向图中，单个负边权值会产生一个负循环。

另请参阅

||||

介绍了R2015b

MATLAB的文档

万博1manbetx

介绍基于MATLAB的深度学习

介绍基于MATLAB的深度学习

下载电子书