工厂，仓库，销售分配模型:基于问题的

这个例子展示了如何建立和解决一个混合整数线性规划问题。问题是在一组工厂、仓库和销售网点之间找到最优的生产和分销水平。关于基于求解器的方法，请参见工厂，仓库，销售分配模型:基于求解器．

该示例首先为工厂、仓库和销售网点生成随机位置。可以随意修改缩放参数 $N$ ，它既可以缩放生产和配送设施所在的网格的大小，也可以缩放这些设施的数量，以便每个网格区域内每种类型的设施密度是独立的 $N$ ．

设施位置

对于给定的缩放参数值 $N$ ，假设有以下情况:

$⌊ f N^{2} ⌋$ 工厂
$⌊ w N^{2} ⌋$ 仓库
$⌊ 年代 N^{2} ⌋$ 销售网点

这些设施位于1和之间的单独整数网格点上 $N$ 在 $x$ 和 $y$ 的方向。为了让这些设施有单独的位置，你需要这样做 $f + w + 年代 \leq 1$ ．在本例中，取 $N ＝ 20$ ， $f ＝ 0 ． 05$ ， $w ＝ 0 ． 05$ , $年代＝ 0 ． 1$ ．

生产和销售

有 $P$ s manbetx 845工厂生产的产品。取 $P ＝ 20$ ．

每一种产品的需求 $p$ 在销售部门 $年代$ 是 $d （年代， p)$ ．需求是一段时间内可以出售的数量。模型的一个约束条件是需求得到满足，这意味着系统生产和分配的数量恰好满足需求。

每个工厂和每个仓库都有容量限制。

产品的生产 $p$ 在工厂 $f$ 小于 $p c 一个 p （ f ， p)$ ．
仓库容量 $w$ 是 $w c 一个 p （ w)$ ．
产品数量 $p$ 可以从仓库运输 $w$ 给一个销售网点的时间间隔小于 $t u r n （ p) ＊ w c 一个 p （ w)$ ,在那里 $t u r n （ p)$ 产品的周转率是多少 $p$ ．

假设每个销售网点只从一个仓库接收供应品。问题的一部分是确定销售网点到仓库的最便宜映射。

成本

从工厂到仓库以及从仓库到销售点运输产品的成本取决于s manbetx 845设备之间的距离，以及具体的产品。如果 $d 我年代 t （一个， b)$ 设施之间的距离如何 $一个$ 和 $b$ ，然后是产品的运输成本 $p$ 这些设施之间的距离乘以运输成本 $t c o 年代 t （ p)$ ：

$d 我年代 t （一个， b) ＊ t c o 年代 t （ p) ．$

本例中的距离是网格距离，也称为 $l_{1}$ 距离。它是绝对值差的和 $x$ 坐标和 $y$ 坐标。

生产一单位产品的成本 $p$ 在工厂 $f$ 是 $p c o 年代 t （ f ， p)$ ．

优化问题

给定一组设施位置，以及需求和能力限制，发现:

每个工厂每种产品的生产水平
产品从工厂到仓库的分配时间表s manbetx 845
产品从仓库到销售点的分配时间表s manbetx 845

这些数量必须确保满足需求和总成本最小化。而且，每个销售网点必须从一个仓库接收所有产品。s manbetx 845

最优化问题的变量和方程

控制变量，也就是你可以在优化过程中改变的变量

$x （ p ， f ， w)$ 产品的数量 $p$ 那是从工厂运来的 $f$ 到仓库 $w$
$y （年代， w)$ =一个值为1的二元变量 $年代$ 与仓库相关 $w$

最小化的目标函数为

$\sum_{f} \sum_{p} \sum_{w} x （ p ， f ， w) \cdot （ p c o 年代 t （ f ， p) + t c o 年代 t （ p) \cdot d 我年代 t （ f ， w))$

$+ \sum_{年代} \sum_{w} \sum_{p} （ d （年代， p) \cdot t c o 年代 t （ p) \cdot d 我年代 t （年代， w) \cdot y （年代， w)) ．$

的约束

$\sum_{w} x （ p ， f ， w) \leq p c 一个 p （ f ， p)$ (工厂)的能力。

$\sum_{f} x （ p ， f ， w) ＝ \sum_{年代} （ d （年代， p) \cdot y （年代， w))$ (满足需求)。

$\sum_{p} \sum_{年代} \frac{d （年代， p)}{t u r n （ p)} \cdot y （年代， w) \leq w c 一个 p （ w)$ (仓库)的能力。

$\sum_{w} y （年代， w) ＝ 1$ (每个销售网点对应一个仓库)。

$x （ p ， f ， w) \geq 0$ (非负生产)。

$y （年代， w) ϵ ｛ 0 ， 1 ｝$ (二进制 $y$ )．

的变量 $x$ 和 $y$ 线性地出现在目标函数和约束函数中。因为 $y$ 问题是一个混合整数线性规划(MILP)。

产生一个随机问题:设施位置

的值 $N$ ， $f$ ， $w$ , $年代$ 参数，并生成设施位置。

rng (1)%的再现性N = 20;% N从10到30似乎有效。谨慎选择大的值。N2 = N * N;f = 0.05;工厂密度%w = 0.05;仓库密度%s = 0.1;销售网点密度%F =地板(F * N2);%工厂数量W =地板(W * N2);%仓库数量S =地板(S * N2);%销售网点数量xyloc = randperm (N2, F + W + S);独特的设施位置[xloc,yloc] = ind2sub([N N]，xyloc);

当然，随机选择设施地点是不现实的。本示例旨在展示解决方案技术，而不是如何生成良好的设施位置。

情节的设施。设施1到F是工厂，F+1到F+W是仓库，F+W+1到F+W+S是销售网点。

h =图;情节(xloc (1: F), yloc (1: F),“rs”xloc (F + 1: F + W), yloc (F + 1: F + W),“k *’，．..xloc (F + W + 1: F + W + S), yloc (F + W + 1: F + W + S),“波”）;lgnd =传奇(“工厂”，“仓库”，“销售渠道”，“位置”，“EastOutside”）;lgnd。自动更新=“关闭”；xlim ([0 N + 1]); ylim ([0 N + 1])

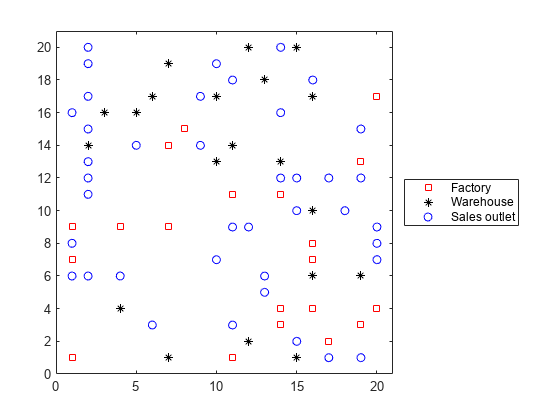
图中包含一个坐标轴。轴线包含3个线型对象。这些对象代表工厂、仓库、销售网点。

随机生成容量、成本和需求

产生随机的生产成本、产能、周转率和需求。

P = 20;% 20产s manbetx 845品%生产成本在20至100之间pcost = 80*rand(F,P) + 20;%每个产品/工厂的生产能力在500到1500之间pcap = 1000*rand(F,P) + 500;%每个产品/仓库在P*400和P*800之间的仓库容量wcap = P*400*rand(W,1) + P*400;%每个产品的周转率在1到3之间= 1 *rand(1,P) + 1;%每件产品的运输成本在5到10之间tcost = 5*rand(1,P) + 5;%各销售网点的产品需求在200 - 500之间%的产品/出口d = 300*rand(S,P) + 200;

这些随机的需求和能力可能导致不可行的问题。换句话说，有时需求超过了生产和仓库容量的限制。如果你改变一些参数，得到一个不可行的问题，在解决过程中，你将得到一个退出标志-2。

生成变量和约束

要开始指定问题，请生成距离数组distfw (i, j)和distsw (i, j)．

distfw = 0 (F, W);按工厂-仓库距离分配矩阵为2 = 1: F为jj = 1:W disfw (ii,jj) = abs(xloc(ii) - xloc(F + jj)) + abs(yloc(ii))．..- yloc(F + jj);结束结束distsw = 0 (S, W);%分配销售网点-仓库距离矩阵为2 = 1: S为jj = 1:W dissw (ii,jj) = abs(xloc(F + W + ii) - xloc(F + jj))．..+ abs(yloc(F + W + ii) - yloc(F + jj));结束结束

为优化问题创建变量。x表示生产，一个连续变量，带有维度P——- - - - - -F——- - - - - -W．y表示销售渠道到仓库、仓库和仓库的二元分配年代——- - - - - -W变量。

x = optimvar (“x”, F P W,下界的, 0);y = optimvar (“y”,年代,W,“类型”，“整数”，下界的0,“UpperBound”1);

现在创建约束。第一个约束是生产能力的约束。

Capconstr = sum(x,3) <= pcap';

下一个约束是需求在每个销售网点得到满足。

Demconstr = squeeze(sum(x,2)) == d'*y;

每个仓库都有容量限制。

wrecap = sum(diag(1./turn)*(d'*y)，1) <= wcap';

最后，还要求每个销售网点精确地连接到一个仓库。

salesware = sum(y,2) = ones(S,1);

创造问题和目标

创造一个优化问题。

factoryprob = optimproblem;

目标函数由三部分组成。第一部分是生产成本的总和。

objfun1 =(金额(金额总和(x) 3)。* (pcost”),2),1);

第二部分是工厂到仓库的运输成本之和。

objfun2 = 0;为p = 1: p objfun2 = objfun2 + tcost (p) *金额(金额(挤压(x (p::)。* distfw));结束

第三部分是仓库到销售点的运输成本之和。

r =总和(distsw。* y, 2);% r是一个长度s的向量v = d * (tcost (:));objfun3 = (v * r)之和;

最小化的目标函数是这三部分之和。

factoryprob。对象= objfun1 + objfun2 + objfun3;

在问题中包含约束条件。

factoryprob.Constraints.capconstr = capconstr;factoryprob.Constraints.demconstr = demconstr;factoryprob.Constraints.warecap = warecap;factoryprob.Constraints.salesware = salesware;

解决这个问题

关闭迭代显示，这样就不会得到几百行输出。包含一个绘图功能来监视解决方案的进度。

选择= optimoptions (“intlinprog”，“显示”，“关闭”，“PlotFcn”, @optimplotmilp);

调用求解器来找到解决方案。

[溶胶,fval exitflag、输出]=解决(factoryprob,“选项”、选择);

图优化Plot函数包含一个轴。最佳目标:3.0952e+07，相对间隙:0。包含4个类型为line的对象。这些对象代表Root LB, Cuts LB, Heuristics UB, New Solution。

如果isempty (sol)如果问题不可行，或者你因为没有解决方案而提前停止disp (解算器没有返回解。)返回%停止脚本，因为没有要检查的内容结束

检查解决方案

检查退出标志和解决方案的不可行性。

exitflag

exitflag = OptimalSolution

infeas1 = max (max(不可行性(capconstr,索尔)))

infeas1 = 9.0949 e-13

infeas2 = max (max(不可行性(demconstr,索尔)))

infeas2 = 8.0718 e-12

infeas3 = max(不可行性(warecap,索尔))

infeas3 = 0

infeas4 = max(不可行性(salesware,索尔))

infeas4 = 2.4425 e15汽油

在y解的一部分是整数值。要理解为什么这些变量可能不是整数，请参见一些“整数”解不是整数万博尤文图斯．

sol.y =圆(sol.y);得到整数解万博 尤文图斯

每个仓库有多少销售网点?请注意，在本例中，有些仓库有0个关联出口，这意味着在最佳解决方案中没有使用这些仓库。

媒体=总和(sol.y, 1)

媒体=1×202 0 3 2 2 2 2 3 3 2 1 0 0 3 4 3 2 3 2 2 1

绘制每个销售网点与仓库之间的联系图。

图(h);持有在为ii = 1:S jj = find(sol.y(ii，:));与ii相关的仓库指数%xsales = xloc (F + W + 2);ysales = yloc (F + W + 2);xwarehouse = xloc (F + jj);ywarehouse = yloc (F + jj);如果兰特(1)< 0。5前半段时间画y方向情节([xsales、xsales xwarehouse], [ysales、ywarehouse ywarehouse),“g——”)其他的%其余时间先画x方向情节([xsales、xwarehouse xwarehouse], [ysales、ysales ywarehouse),“g——”)结束结束持有从标题(“销售网点到仓库的映射”)