问题概述

正如Markowitz所展示的(《投资组合选择》，J. Finance卷7，第1期，77-91页，1952年3月)，你可以用二次规划问题来表达许多投资组合优化问题。假设你有一组N要选择资产组合，要有资产搭配 $$x（我）$$这是你投资的一部分资产 $$我$$．如果你知道这个向量 $$r$$每个资产的平均收益，和协方差矩阵 $$问$$在一定的风险规避水平下 $$\lambda$$将风险调整后的预期收益最大化:

的quadprog求解器解决了这个二次规划问题。然而，除了简单的二次规划问题之外，你可能还想以各种方式限制一个投资组合，例如:

您不能将这些约束包含在quadprog．困难在于约束条件的离散性。此外，混合整数线性规划求解器intlinprog不处理离散约束，不处理二次目标函数。

本例构造了一系列满足约束条件的MILP问题，并逐渐逼近二次目标函数。虽然这种技术适用于本例，但它可能不适用于不同的问题或约束类型。

从约束建模开始。

离散约束建模

$$x$$是资产配置的分量，与 $$0\le x（我）\le 1$$为每一个 $$我$$．要对投资组合中的资产数量建模，您需要指标变量 $$v$$这样 $$v（我）＝0$$当 $$x（我）＝0$$, $$v（我）＝1$$当 $$x（我）>0$$．要获得满足此限制的变量，请设置 $$v$$向量是一个二进制变量，并施加线性约束

这些不平等都加强了这一点 $$x（我）$$而且 $$v（我）$$同时是零吗，他们也强制这么做吗 $$f米我n\le x（我）\le f米\mathrm{一个}x$$每当 $$x（我）>0$$．

此外，为了加强对投资组合中资产数量的约束，需要施加线性约束

目标和连续线性逼近

根据最初的公式，你要尽量使目标函数最大化。然而，所有优化工具箱™求解器都最小化。所以把这个问题表述为最小化目标的负面影响:

这个目标函数是非线性的。的intlinprogMILP求解器需要一个线性目标函数。有一种标准的技术可以将这个问题重新表述为具有线性目标和非线性约束的问题。引入松弛变量 $$z$$来表示二次项。

当您迭代求解MILP近似时，您将包含新的线性约束，每个约束都近似于当前点附近的局部非线性约束。特别是，对于 $$x＝x_0+\delta$$在哪里 $$x_0$$是常数向量和吗 $$\delta$$是一个变向量，约束的一阶泰勒近似是

替换 $$\delta$$通过 $$x-x_0$$给了

对于每个中间溶液 $$x_k$$引入一个新的线性约束 $$x$$而且 $$z$$如上面表达式的线性部分:

这是一个形式 $$\mathrm{一个}x\le b$$,在那里 $$\mathrm{一个}＝2x_k^T问$$，有一个 $$-1$$的乘数 $$z$$项, $$b＝x_k^T问x_k$$．

这种在问题中加入新的线性约束的方法叫做切平面法。详情请参阅小J. E.凯利。求解凸规划的切平面法。j . Soc。工业上。达成。数学。1960年12月，第八卷第四期，703-712页。

MATLAB®问题公式

表达问题intlinprog求解器，你需要做以下事情:

拥有第一个 $$N$$变量表示 $$x$$向量，下一个 $$N$$变量表示二进制 $$v$$向量，最后一个变量表示 $$z$$松弛变量。有 $$2N+1$$问题中的变量。

加载问题的数据。该数据在向量中有225个预期收益r225 × 225矩阵中收益的协方差问．数据与在投资组合优化问题上使用二次规划的例子相同。

负载port5R = mean_return;Q = Correlation .* (stdDev_return * stdDev_return');

将资产数量设置为N．

N =长度(r);

为变量设置索引

xvars = 1:N;vvars = N+1:2*N;zvar = 2*N+1;

的下界2 n + 1问题中的变量为零。第一个的上界2 n变量是一个，最后一个变量没有上界。

lb = 0 (2*N+1,1);ub = ones(2*N+1,1);ub(zvar) = Inf;

将解决方案中的资产数量设置为100到150之间。将这个约束合并到表单中的问题中，即

通过写出两个线性约束条件的形式 $$\mathrm{一个}x\le b$$：

M = 150;M = 100;A = 0 (1,2*N+1);%分配一个矩阵A(vvars) = 1;% A*x表示v(i)的和A = [A; -a];B = 0 (2,1);分配b向量b(1) = M;B (2) = -m;

包括半连续约束。取资产的最小非零部分为0.001对于每一种资产类型，最大的比例是0.05．

Fmin = 0.001;Fmax = 0.05;

包括不平等 $$x（我）\le f米\mathrm{一个}x（我）＊v（我）$$而且 $$f米我n（我）＊v（我）\le x（我）$$作为线性不等式。

Atemp =眼(N);Amax = horzcat(Atemp，-Atemp*fmax，零(N,1));A = [A;Amax];b = [b; 0 (N,1)];Amin = horzcat(-Atemp,Atemp*fmin，零(N,1));A = [A;Amin];b = [b; 0 (N,1)];

包括投资组合100%投资的约束，这意味着 $$\sum x_{我}＝1$$．

Aeq = 0 (1,2*N+1);分配Aeq矩阵Aeq(xvars) = 1;Beq = 1;

设置风险规避系数 $$\lambda$$来One hundred.．

λ = 100;

定义目标函数 $$\lambda z-r^{T}x$$作为一个向量。的乘数要包含零 $$v$$变量。

f = [-r; 0 (N,1);lambda];

解决问题

要迭代地解决这个问题，首先要用当前的约束条件来解决这个问题，这些约束条件还没有反映出任何线性化。整数约束在vvars向量。

选项= optimoptions(@intlinprog，“显示”，“关闭”）;%抑制迭代显示[xLinInt,fval,exitFlagInt,output] = intlinprog(f,vvars,A,b,Aeq,beq,lb,ub,options);

为迭代准备一个停止条件:当松弛变量时停止 $$z$$在真实二次值的0.01%内。设置比默认值更严格的公差，以帮助确保随着约束的积累，问题仍然严格可行。

Thediff = 1e-4;Iter = 1;%迭代计数器assets = xLinInt(xvars);% x变量真二分=资产的*Q*资产;zslack = xLinInt(zvar);%松弛变量值Options = optimoptions(Options，“LPOptimalityTolerance”1平台以及“RelativeGapTolerance”1 e-8.．.“ConstraintTolerance”1 e-9“IntegerTolerance”1 e-6);

保存计算出的真二次元和松弛变量的历史，以便绘图。

历史= [truequadratic,zslack];

计算二次元和松弛值。如果它们不一致，则添加另一个线性约束并再次求解。

在工具箱语法中，每一个新的线性约束 $$\mathrm{一个}x\le b$$来自于线性近似

你看，新的一行 $$\mathrm{一个}＝2x_k^T问$$新元素 $$b＝x_k^T问x_k$$，与 $$z$$的-1系数表示的项 $$\mathrm{一个}$$．

找到新解后，在新旧解之间使用一个线性约束。万博 尤文图斯这种包含线性约束的启发式方法比简单地采用新解更快。要使用该解决方案而不是中途启发式，请注释下面的“中途”行，并取消注释下面的行。

而Abs ((zslack - true equadatic)/true equadatic) > thediff相对误差%newArow = horzcat(2*assets'*Q, 0 (1,N)，-1);%线性化约束rhs =资产'*Q*资产;%在线性化约束的右边A = [A;newArow];B = [B;r];用新的约束条件解决问题。[xLinInt,fval,exitFlagInt,output] = intlinprog(f,vvars,A,b,Aeq,beq,lb,ub,options);assets = (assets+xLinInt(xvars))/2;从前到现在的中途。% assets = xLinInt(xvars);使用前一行或这一行true equadatic = xLinInt(xvars)'*Q* xLinInt(xvars);zslack = xLinInt(zvar);历史=[历史;真赤道，zslack];Iter = Iter + 1;结束

检验解和收敛速度

绘制松弛变量和目标函数的二次函数部分的历史图，看看它们是如何收敛的。

情节(历史)传说(“二次”，“松弛”)包含(的迭代次数)标题(“二次和线性逼近(松弛)”）

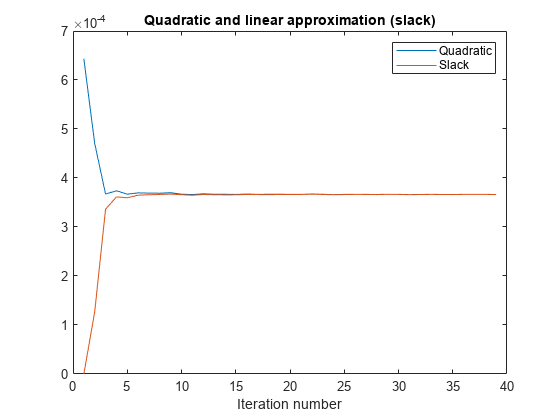
MILP解决方案的质量如何?的输出结构包含该信息。检查在解处目标上的内部计算边界之间的绝对间隙。

disp (output.absolutegap)

0

绝对差为零，说明MILP解是准确的。

绘制最优分配图。使用xLinInt (xvars),而不是资产,因为资产在使用中途更新时可能不满足约束。

栏(xLinInt (xvars))网格在包含(“资产指数”) ylabel (“投资比例”)标题(“最优资产配置”）

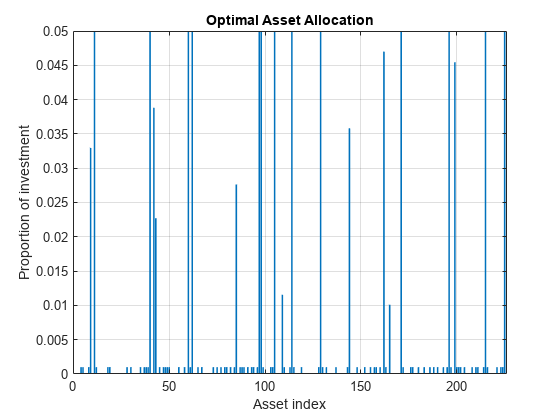
你可以很容易地看到，所有非零资产配置都在半连续边界之间 $$f米我n＝0．001$$而且 $$f米\mathrm{一个}x＝0．05$$．

有多少非零资产?限制是有100到150个非零资产。

sum (xLinInt (vvars))

Ans = 100

这个配置的预期收益是多少?风险调整后的收益值是多少?

流('预期收益为%g，经风险调整的收益为%g。\n'，.．.r * xLinInt (xvars)、-fval)

预期收益为0.000595107，风险调整后收益为-0.0360382。

通过使用Financial Toolbox™中专门为投资组合优化设计的特性，可以进行更详细的分析。有关演示如何使用Portfolio类直接处理半连续约束和基数约束的示例，请参见具有半连续和基数约束的投资组合优化(金融工具箱)．