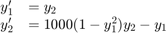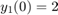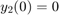主要内容
ode23t
求解中等刚度ODE和DAE-梯形规则
语法
描述
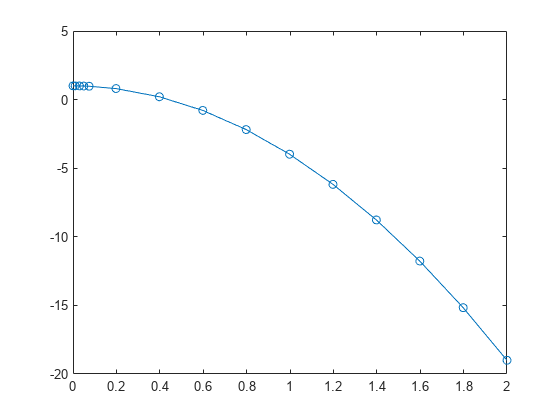
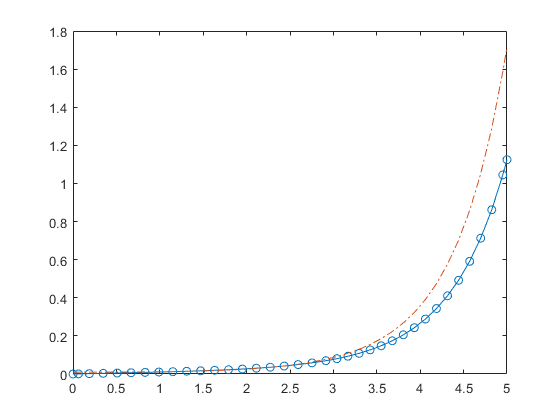
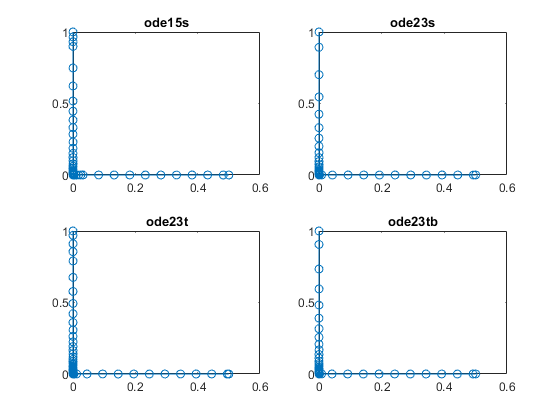
例子
输入参数
输出参数
参考文献
L. F., M. W. Reichelt, J.A. Kierzenka, "在MATLAB和Simulink中求解索引-1 DAE万博1manbetx",暹罗审查, 1999年第41卷,第538-552页。
[2] Shampine, L. F. and M. E. Hosea,“TR-BDF2的分析与实现”,应用数值数学20, 1996年。
另请参阅
之前介绍过的R2006a