设施位置

对于缩放参数的给定值 $$N$$，假设有以下内容：

这些设施在1之间的单独整数网格点上 $$N$$在里面 $$X$$和 $$y$$方向。为了使设施具有独立的位置，您需要 $$F+\mathrm{W.}+\mathrm{S.}\le .1$$。在这个例子中，采取 $$N=20.$$那 $$F=0.。0.5.$$那 $$\mathrm{W.}=0.。0.5.$$， 和 $$\mathrm{S.}=0.。1$$。

生产和分销

有 $$\mathrm{P.}$$s manbetx 845产品制造的产品。拿 $$\mathrm{P.}=20.$$。

对每个产品的需求 $$\mathrm{P.}$$在销售出口 $$\mathrm{S.}$$是 $$\mathrm{D.}（\mathrm{S.}那\mathrm{P.}）$$。需求是可以在时间间隔销售的数量。对模型的一个约束是满足需求，这意味着系统产生并分发需求中的数量。

每个工厂和每个仓库都有容量限制。

假设每个销售插座从一个仓库收到其耗材。部分问题是确定销售网点的最便宜映射到仓库。

成本

从工厂到仓库的产品的成本以及从仓库到销售店，取决于s manbetx 845设施与特定产品之间的距离。如果 $$\mathrm{D.}\mathrm{一世}\mathrm{S.}\mathrm{T.}（\mathrm{一种}那\mathrm{B.}）$$是设施之间的距离 $$\mathrm{一种}$$和 $$\mathrm{B.}$$，然后运送产品的成本 $$\mathrm{P.}$$这些设施之间是运输成本的距离次数 $$\mathrm{T.}C\mathrm{O.}\mathrm{S.}\mathrm{T.}（\mathrm{P.}）$$：

该示例中的距离是网格距离，也称为 $${\mathrm{L.}}_1$$距离。这是绝对差异的总和 $$X$$坐标和 $$y$$坐标。

制作产品单位的成本 $$\mathrm{P.}$$在工厂 $$F$$是 $$\mathrm{P.}C\mathrm{O.}\mathrm{S.}\mathrm{T.}（F那\mathrm{P.}）$$。

优化问题

给定一套设施位置，以及需求和容量约束，查找：

这些数量必须确保满足需求，并且总成本最小化。此外，每个销售渠道都需要从一个仓库中收到所有产品。s manbetx 845

优化问题的变量和方程

控制变量，这意味着您可以在优化中更改的变量

最小化的目标函数是

约束是

$$\underset{\mathrm{W.}}{\sigma .}X（\mathrm{P.}那F那\mathrm{W.}）\le .\mathrm{P.}C\mathrm{一种}\mathrm{P.}（F那\mathrm{P.}）$$（工厂的产能）。

$$\underset{F}{\sigma .}X（\mathrm{P.}那F那\mathrm{W.}）=\underset{\mathrm{S.}}{\sigma .}（\mathrm{D.}（\mathrm{S.}那\mathrm{P.}）\cdot y（\mathrm{S.}那\mathrm{W.}））$$（满足需求）。

$$\underset{\mathrm{P.}}{\sigma .}\underset{\mathrm{S.}}{\sigma .}\frac{\mathrm{D.}（\mathrm{S.}那\mathrm{P.}）}{\mathrm{T.}你\mathrm{R.}N（\mathrm{P.}）}\cdot y（\mathrm{S.}那\mathrm{W.}）\le .\mathrm{W.}C\mathrm{一种}\mathrm{P.}（\mathrm{W.}）$$（仓库的容量）。

$$\underset{\mathrm{W.}}{\sigma .}y（\mathrm{S.}那\mathrm{W.}）=1$$（每个销售分配给一个仓库）。

$$X（\mathrm{P.}那F那\mathrm{W.}）\ge 0.$$（非负生产）。

$$y（\mathrm{S.}那\mathrm{W.}）\mathrm{\epsilon .}\{0.那1\}$$（二进制 $$y$$）。

变量 $$X$$和 $$y$$线性出现在目标和约束函数中。因为 $$y$$仅限于整数值，问题是混合整数线性程序（MILP）。

生成随机问题：设施位置

设置值的值 $$N$$那 $$F$$那 $$\mathrm{W.}$$， 和 $$\mathrm{S.}$$参数，并生成设施位置。

RNG（1）重复性的％n = 20;似乎从10到30之间的％n工作。小心选择大值。n2 = n * n;f = 0.05;％密度的工厂w = 0.05;仓库密度％s = 0.1;销售网点的％密度f =地板（f * n2）;％的工厂数量W =地板（W * N2）;％仓库数量S =地板（S * N2）;％销售网点数量XYLOC = RANDPERM（N2，F + W + S）;％独特的设施位置[XLOC，YLOC] = IND2SUB（[N N]，XYLOC）;

当然，采取随机的设施的随机地点并不现实。此示例旨在显示解决方案技术，而不是如何生成良好的设施位置。

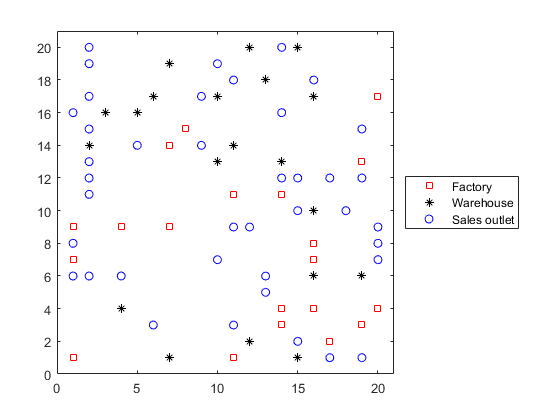
绘制设施。设施1到F是工厂，F + 1至F + W是仓库，F + W + 1至F + W + S是销售网点。

h =图;绘图（XLOC（1：F），Yloc（1：F），'rs'，XLOC（F + 1：F + W），YLOC（F + 1：F + W），'k *'那......XLOC（F + W + 1：F + W + S），YLOC（F + W + 1：F + W + S），'博'）;lgnd =图例（'工厂'那'仓库'那'销售出口'那'地点'那'eastoutside'）;lgnd.autoupdate =.'离开';XLIM（[0 n + 1]）; ylim（[0 n + 1]）

生成随机能力，成本和需求

产生随机生产成本，容量，营业额，需求。

p = 20;％20产品s manbetx 845％生产成本20到100之间pcost = 80 * rand（f，p）+ 20;每种产品/工厂的500平方程的产能率为500和1500PCAP = 1000 * RAND（F，P）+ 500;每个产品/仓库的P * 400和P * 800之间的％仓库容量WCAP = P * 400 * RAND（W，1）+ P * 400;每种产品的1和3之间的％产品变化率转= 2 * rand（1，p）+ 1;每种产品的每距离5到10的产品运输成本tcost = 5 * rand（1，p）+ 5;每次销售插座的产品需求量为200％至500％产品/出口d = 300 * rand（s，p）+ 200;

这些随机需求和容量可能导致不可行的问题。换句话说，有时需求超过了生产和仓库容量限制。如果您更改了一些参数并获得了一个不可行的问题，在解决方案期间，您将获得-2的ExitFlag。

生成目标和约束矩阵和向量

目标函数矢量obj.在Intlincon.由变量的系数组成 $$X（\mathrm{P.}那F那\mathrm{W.}）$$和 $$y（\mathrm{S.}那\mathrm{W.}）$$。所以天然存在p * f * w + s * w系数obj.。

生成系数的一种方法是从一个开始p-by-fy-w大批obj1.为了 $$X$$系数，和一个S-BY-W大批obj2.为了 $$y（\mathrm{S.}那\mathrm{W.}）$$系数。然后将这些阵列转换为两个向量并将它们组合成obj.通过呼叫

obj = [obj1（:); obj2（:)];

obj1 =零（p，f，w）;％分配阵列obj2 = zeros（s，w）;

在整体一代的客观和约束矢量和矩阵中，我们产生了 $$（\mathrm{P.}那F那\mathrm{W.}）$$阵列或阵列 $$（\mathrm{S.}那\mathrm{W.}）$$数组，然后将结果转换为向量。

要开始生成输入，请生成距离阵列distfw（i，j）和DISTSW（I，J）。

distfw =零（f，w）;％分配用于工厂仓库距离的矩阵为了II = 1：f为了JJ = 1：w distfw（ii，jj）= abs（xloc（ii） -  xloc（f + jj））+ abs（yloc（ii）......-  Yloc（F + JJ））;结尾结尾distsw =零（s，w）;％分配矩阵用于销售Outlet-Warehouse距离为了II = 1：s为了JJ = 1：W DISTSW（II，JJ）= ABS（XLOC（F + W + II） -  XLOC（F + JJ））......+ ABS（YLOC（F + W + II） -  YLOC（F + JJ））;结尾结尾

生成条目obj1.和obj2.。

为了II = 1：p为了JJ = 1：F为了KK = 1：W OBJ1（II，JJ，KK）= PCOST（JJ，II）+ TCOST（II）* DISTFW（JJ，KK）;结尾结尾结尾为了II = 1：s为了JJ = 1：W OBJ2（II，JJ）= DistSW（II，JJ）*和（D（II，：）。* Tcost）;结尾结尾

将条目组合成一个矢量。

obj = [obj1（:); obj2（:)];％obj是目标函数矢量

现在创建约束矩阵。

每个线性约束矩阵的宽度是obj.向量。

matwid =长度（obj）;

线性不等式有两种类型：生产能力约束，以及仓库容量约束。

有P * F.生产能力约束，和W.仓库容量约束。约束矩阵非常稀疏，大约1％非零的顺序，因此使用稀疏矩阵保存内存。

Aineq = spalloc（p * f + w，matwid，p * f * w + s * w）;％分配稀疏AEQbineq =零（p * f + w，1）;％将bineq分配完整尺寸方便的零矩阵：lemener1 = zeros（尺寸（obj1））;clearer12 = clearer1（:);lemener2 =零（尺寸（obj2））;Clearer22 = Clearer2（:);％首先生产容量约束计数器= 1;为了II = 1：f为了JJ = 1：p xtemp = lemener1;XTEMP（JJ，II，:) = 1;每个产品和工厂的仓库百分比xtemp =稀疏（[xtemp（:); clearer22]）;％转换为稀疏Aineq（计数器，:) = XTEMP';％填写Bineq（计数器）= PCAP（II，JJ）;计数器=计数器+ 1;结尾结尾百分比现在仓库容量约束vj =零（s，1）;％乘数为了JJ = 1：S VJ（JJ）= SUM（D（JJ，:) ./转弯）;％p元素的总和结尾为了II = 1：W XTEMP =更清晰;XTEMP（：，ii）= vj;xtemp =稀疏（[更清晰的12; xtemp（:)]）;％转换为稀疏Aineq（计数器，:) = XTEMP';％填写Bineq（计数器）= WCAP（II）;计数器=计数器+ 1;结尾

有两种类型的线性平等约束：满足需求的约束，以及每个销售插座对应于一个仓库的约束。

AEQ = spalloc（p * w + s，matwid，p * w *（f + s）+ s * w）;％分配为稀疏beq =零（p * w + s，1）;％分配向量计数器= 1;需求需求满足：为了II = 1：p为了JJ = 1：W XTEMP =更清晰;XTEMP（II，：，JJ）= 1;xtemp2 =更清晰的2;XTEMP2（：，JJ）= -D（：，II）;xtemp = sparse（[xtemp（:); xtemp2（:)]）;％变为稀疏行AEQ（计数器，:) = XTEMP;％填写计数器=计数器+ 1;结尾结尾每次销售渠道只有一个仓库：为了II = 1：S XTEMP =更清晰;XTEMP（II，:) = 1;XTEMP =稀疏（[透明器12; XTEMP（:)]）;％变为稀疏行AEQ（计数器，:) = XTEMP;％填写Beq（计数器）= 1;计数器=计数器+ 1;结尾

绑定约束和整数变量

整数变量是那些来自的变量长度（obj1）+ 1到最后。

INTCON = P * F * W + 1：长度（OBJ）;

上限来自长度（obj1）+ 1到底也。

lb =零（长度（obj），1）;UB = INF（长度（obj），1）;UB（P * F * W + 1：END）= 1;

关闭迭代显示，以便您没有获得数百行输出。包括监视解决方案进度的绘图功能。

opts = Optimoptions（'intlinprog'那'展示'那'离开'那'plotfcn'，@ Optimplotmilp）;

解决这个问题

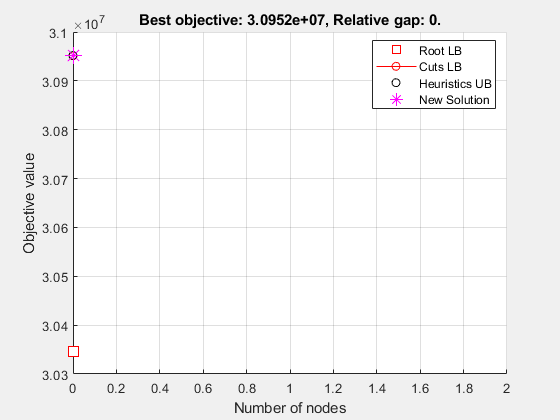
您生成了所有求解器输入。调用求解器查找解决方案。

[解决方案，FVAL，EXITFLAG，输出] = INTLINPROG（OBJ，INTCON，......Aineq，Bineq，AEQ，BEQ，LB，UB，OPTS）;

如果Isempty（解决方案）％如果问题是不可行的，或者您早期停止没有解决方案DISP（'intlinprog没有返回解决方案。）返回％停止脚本，因为没有什么可以检查结尾

检查解决方案

解决方案是可行的，在给定的公差范围内。

ExitFlag.

EXITFLAG = 1

Infeas1 = Max（Aineq *解决方案 -  Bineq）

Infeas1 = 8.2991e-12

Infeas2 = Norm（AEQ *解决方案 -  BEQ，INF）

Infeas2 = 1.6428E-11

检查整数组件是否真实整数，或者足够接近，舍入舍入。要了解为什么这些变量可能不是完全整数，请参阅一些“整数”解决方案不是整数万博 尤文图斯。

Diffint = Norm（解决方案（INTCON） - 圆形（解决方案（INTCON）），INF）

闪烁= 1.1990E-13

一些整数变量不是完全整数，但一切都非常接近。所以围绕整数变量。

解决方案（INTCON）=圆形（解决方案（INTCON））;

检查圆形解决方案的可行性以及客观函数值的变化。

Infeas1 = Max（Aineq *解决方案 -  Bineq）

Infeas1 = 8.2991e-12

Infeas2 = Norm（AEQ *解决方案 -  BEQ，INF）

Infeas2 = 5.8435e-11

diffrounding = norm（fval  -  obj（:)'* solution，inf）

Diffrounding = 1.8626E-08

舍入解决方案并未明显改变其可行性。

您可以通过重新恢复其原始尺寸来检查解决方案。

solution1 =解决方案（1：p * f * w）;％连续变量solution2 =解决方案（INTCON）;％整数变量solution1 = Rehape（Solution1，P，F，W）;solution2 =重塑（solution2，s，w）;

例如，每个仓库都关联多少个销售商店？请注意，在这种情况下，某些仓库具有0个相关插座，这意味着仓库不在最佳解决方案中使用。

Outlets = sum（solution2,1）销售商网点上的％总和

outlets =1×203 0 3 2 2 2 3 2 3 1 1 0 0 3 4 3 2 3 2 1

绘制每个销售插座和其仓库之间的连接。

图（h）;抓住在为了II = 1：S JJ =查找（解决方案2（II，:)）;与II相关的仓库的％指数XSALES = XLOC（F + W + II）;ysales = yloc（f + w + ii）;XWAREHOUSE = XLOC（F + JJ）;ywarehouse = yloc（f + jj）;如果兰特（1）<.5％在上半场抽出y方向plot（[xsales，xsales，xwarehouse]，[ysales，ywarehouse，ywarehouse]，'G - '）别的首先绘制X方向的其余时间plot（[xsales，xwarehouse，xwarehouse]，[ysales，ysales，ywarehouse]，'G - '）结尾结尾抓住离开标题（“销售网点绘制到仓库”）

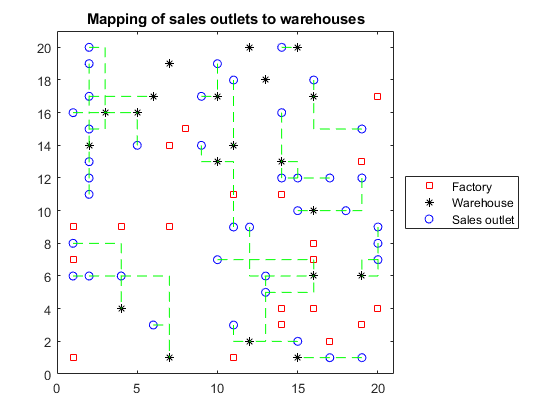
黑色*没有绿线代表未使用的仓库。