定义你的使用稀疏矩阵线性方程组GydF4y2Ba

当您使用GydF4y2Ba分散式GydF4y2Ba功能，MATLAB自动开始使用默认的群集设置一个平行的泳池。此示例使用Wathen矩阵从MATLABGydF4y2Ba画廊GydF4y2Ba功能。该矩阵是稀疏的，对称的，并与整体尺寸的随机矩阵GydF4y2Ba $$\mathrm{ñGydF4y2Ba}=GydF4y2Ba\mathrm{3GydF4y2Ba}{\mathrm{ñGydF4y2Ba}}^{\mathrm{2GydF4y2Ba}}+GydF4y2Ba\mathrm{4GydF4y2Ba}\mathrm{ñGydF4y2Ba}+GydF4y2Ba\mathrm{1GydF4y2Ba}$$。GydF4y2Ba

N = 400;分布A =（廊（GydF4y2Ba'wathen'GydF4y2Ba，N，N））;GydF4y2Ba

开始使用“本地”轮廓平行池（parpool）......连接到并行池（工号：6）。GydF4y2Ba

N = 3 * N ^ 2 + 4 * n + 1个GydF4y2Ba

N = 481601GydF4y2Ba

现在，您可以定义右手矢量GydF4y2Ba $$\mathrm{bGydF4y2Ba}$$。在这个例子中，GydF4y2Ba $$\mathrm{bGydF4y2Ba}$$被定义为行之和GydF4y2Ba $$\mathrm{一个GydF4y2Ba}$$，这导致精确解GydF4y2Ba $$\mathrm{一个GydF4y2Ba}\mathrm{XGydF4y2Ba}=GydF4y2Ba\mathrm{bGydF4y2Ba}$$形式GydF4y2Ba $${\mathrm{XGydF4y2Ba}}_{\text{精确GydF4y2Ba}}=GydF4y2Ba[GydF4y2Ba\mathrm{1GydF4y2Ba}，GydF4y2Ba。GydF4y2Ba。GydF4y2Ba。GydF4y2Ba，GydF4y2Ba\mathrm{1GydF4y2Ba}{]GydF4y2Ba}^{\mathrm{ŤGydF4y2Ba}}$$。GydF4y2Ba

B =总和（A，2）;GydF4y2Ba

以来GydF4y2Ba和GydF4y2Ba作用的分布式阵列上，GydF4y2BabGydF4y2Ba还分布和其数据存储在您的并行池的工人的记忆。最后，您可以定义使用迭代方法得到的解决方案相比精确解。万博 尤文图斯GydF4y2Ba

xExact =酮（N，1，GydF4y2Ba'分散式'GydF4y2Ba）;GydF4y2Ba

解决您的线性方程组的系统的共轭梯度法GydF4y2Ba

MATLAB函数GydF4y2BaPCGGydF4y2Ba提供了共轭梯度（CG）的方法，其中迭代地生成的一系列的近似解的万博 尤文图斯GydF4y2Ba $\mathit{XGydF4y2Ba}$，提高与每个步骤中的溶液。GydF4y2Ba

[xCG_1，flagCG_1，relres_CG1，iterCG_1，resvecCG_1] = PCG（A，B）;GydF4y2Ba

当系统被解决，可以检查所获得的结果的每个元件之间的误差GydF4y2BaxCG_1GydF4y2Ba和预期值GydF4y2BaxExactGydF4y2Ba。在计算的结果的误差是比较高的。GydF4y2Ba

errCG_1 = ABS（xExact-xCG_1）;图（1）保持GydF4y2Ba离GydF4y2Basemilogy（errCG_1，GydF4y2Ba'O'GydF4y2Ba）;标题（GydF4y2Ba“线性方程组与稀疏矩阵”GydF4y2Ba）;ylabel（GydF4y2Ba“绝对错误”GydF4y2Ba）;xlabel（GydF4y2Ba“元素中X”GydF4y2Ba）;GydF4y2Ba

迭代计算结束时的一系列近似解收敛到特定容差或迭代最大步数后。万博 尤文图斯对于分布式以及在客户端阵列，GydF4y2Ba $$\mathrm{pGydF4y2Ba}\mathrm{CGydF4y2Ba}\mathrm{GGydF4y2Ba}$$使用相同的默认设置：GydF4y2Ba

作为第二输出参数，该GydF4y2BaPCGGydF4y2Ba函数也返回一个收敛标志，让你对所获得的结果的更多信息，包括计算解决方案是否收敛到所需的公差。例如，值GydF4y2Ba0GydF4y2Ba表明该解决方案已适当收敛。GydF4y2Ba

flagCG_1GydF4y2Ba

flagCG_1 = 1GydF4y2Ba

在这个例子中，所述溶液不迭代的默认最大数量，这导致在高误差范围内收敛。GydF4y2Ba

为了提高收敛的可能性，你可以自定义宽容和迭代步最大数的设置。GydF4y2Ba

公差= 1E-12;麦克斯特= N;TCG =抽动;[xCG_2，flagCG_2，relresCG_2，iterCG_2，resvecCG_2] = PCG（A，B，公差，麦克斯特）;TCG = TOC（TCG）;flagCG_2GydF4y2Ba

flagCG_2 = 0GydF4y2Ba

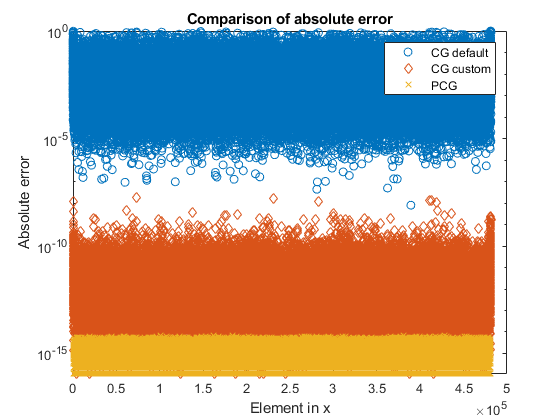
通过自定义设置，解收敛。相比之前的解决方案这种具有改进的绝对误差。GydF4y2Ba

errCG_2 = ABS（xExact-xCG_2）;图（2）保持GydF4y2Ba离GydF4y2Basemilogy（errCG_1，GydF4y2Ba'O'GydF4y2Ba）;保持GydF4y2Ba上GydF4y2Basemilogy（errCG_2，GydF4y2Ba'd'GydF4y2Ba）;标题（GydF4y2Ba“绝对误差的比较”GydF4y2Ba）;ylabel（GydF4y2Ba“绝对错误”GydF4y2Ba）;xlabel（GydF4y2Ba“元素中X”GydF4y2Ba）;传说（GydF4y2Ba“默认宽容和迭代”GydF4y2Ba，GydF4y2Ba“改进的耐受性和迭代”GydF4y2Ba）;保持GydF4y2Ba离GydF4y2Ba

该GydF4y2BaPCGGydF4y2Ba方法还在每个迭代步骤中返回剩余范数的向量，GydF4y2Ba范数（B-A * X）/常态（b）中GydF4y2Ba。相对剩余范示出了连续的迭代步骤之间的精度的比率。残差在迭代过程的演变可以帮助你理解为什么该解决方案也并非没有自定义设置收敛。GydF4y2Ba

图（3）F = semilogy（resvecCG_2./resvecCG_2（1））;保持GydF4y2Ba上GydF4y2Basemilogy（f.Parent.XLim，[1E-6 1E-6]，GydF4y2Ba' - 'GydF4y2Ba）semilogy（[20 20]，f.Parent.YLim，GydF4y2Ba' - 'GydF4y2Ba）semilogy（f.Parent.XLim，[1E-12 1E-12]，GydF4y2Ba' - 'GydF4y2Ba）标题（GydF4y2Ba“相对残余的演变”GydF4y2Ba）;ylabel（GydF4y2Ba“相对残余”GydF4y2Ba）;xlabel（GydF4y2Ba“迭代步骤”GydF4y2Ba）;传说（GydF4y2Ba“CG的残差”GydF4y2Ba，GydF4y2Ba“默认公差”GydF4y2Ba，GydF4y2Ba“默认步数”GydF4y2Ba，GydF4y2Ba“自定义容忍”GydF4y2Ba）保持GydF4y2Ba离GydF4y2Ba

很显然，步骤的默认数量是不够的，实现这个系统很好的解决。GydF4y2Ba

解决您的线性方程组与预处理共轭梯度法GydF4y2Ba

你可以提高使用预处理共轭梯度（PCG）方法解决你的系统的效率。首先，前提你使用预条件矩阵的线性方程组的系统GydF4y2Ba $\mathit{中号GydF4y2Ba}$。其次，解决了使用CG方法的预处理系统。该PCG方法可以比CG方法迭代少得多。GydF4y2Ba

MATLAB函数GydF4y2BaPCGGydF4y2Ba也用于PCG方法。你可以提供一个合适的预条件矩阵GydF4y2Ba $\mathit{中号GydF4y2Ba}$作为一个额外的输入。GydF4y2Ba

一个理想的预条件矩阵是一个矩阵，它的逆GydF4y2Ba ${\mathit{中号GydF4y2Ba}}^{-GydF4y2Ba\mathrm{1GydF4y2Ba}}$是非常近似的系数矩阵的逆矩阵，GydF4y2Ba ${\mathit{一个GydF4y2Ba}}^{-GydF4y2Ba\mathrm{1GydF4y2Ba}}$，但更容易计算。本例使用对角线GydF4y2Ba $$\mathrm{一个GydF4y2Ba}$$线性方程组，以前提的系统。GydF4y2Ba

M = spdiags（spdiags（A，0），0，N，N）;tPCG =抽动;[兵团，flagPCG，relresPCG，iterPCG，resvecPCG] = PCG（A，B，公差，麦克斯特，M）;tPCG = TOC（tPCG）;图（4）保持GydF4y2Ba离GydF4y2Ba;semilogy（resvecCG_2./resvecCG_2（1））保持GydF4y2Ba上GydF4y2Ba;semilogy（resvecPCG./resvecPCG（1））标题（GydF4y2Ba“相对残余的演变”GydF4y2Ba）;ylabel（GydF4y2Ba“相对残余”GydF4y2Ba）;xlabel（GydF4y2Ba“迭代步骤”GydF4y2Ba）;传说（GydF4y2Ba“CG的残差”GydF4y2Ba，GydF4y2Ba'其中M \约DIAG（A）的PCG残差'GydF4y2Ba）GydF4y2Ba

上图显示了PCG方法需要显着更少的步骤收敛相比nonpreconditioned系统。该结果也反映在执行时间。GydF4y2Ba

fprintf中（[GydF4y2Ba...GydF4y2Ba'\ n时间来解决系统CG：％d s' 的GydF4y2Ba，GydF4y2Ba...GydF4y2Ba'\ n时间来解决系统PCG：％d s' 的GydF4y2Ba]，TCG，tPCG）;GydF4y2Ba

时间解决系统CG：1.244593e + 01 s时间解决系统PCG：7.657432e-信息01 SGydF4y2Ba

以及在较少的迭代步骤解决该示例系统中，PCG方法也返回更准确的解决方案。GydF4y2Ba

errPCG = ABS（xExact-兵团）;图（5）保持GydF4y2Ba离GydF4y2Basemilogy（errCG_1，GydF4y2Ba'O'GydF4y2Ba）;保持GydF4y2Ba上GydF4y2Basemilogy（errCG_2，GydF4y2Ba'd'GydF4y2Ba）;semilogy（errPCG，GydF4y2Ba'X'GydF4y2Ba）;标题（GydF4y2Ba“绝对错误的比较”GydF4y2Ba）;ylabel（GydF4y2Ba“绝对错误”GydF4y2Ba）;xlabel（GydF4y2Ba“元素中X”GydF4y2Ba）;传说（GydF4y2Ba“CG默认”GydF4y2Ba，GydF4y2Ba“CG自定义”GydF4y2Ba，GydF4y2Ba'PCG'GydF4y2Ba）;GydF4y2Ba

你与你的计算完成后，您可以删除您的并行池。该GydF4y2BaGCPGydF4y2Ba函数返回当前并行池对象，所以你可以删除当前池。GydF4y2Ba

删除（GCP（GydF4y2Ba'nocreate的'GydF4y2Ba））GydF4y2Ba

在这个例子中使用Wathen矩阵是如何一个良好的预条件可以大大提高解决方案的效率了很好的示范。该Wathen矩阵具有相对小关角分量，所以选择GydF4y2Ba $$\mathrm{中号GydF4y2Ba}=GydF4y2Ba\text{诊断GydF4y2Ba}（GydF4y2Ba\mathrm{一个GydF4y2Ba}）GydF4y2Ba$$给出了一个合适的预处理器。对于任意矩阵GydF4y2Ba $\mathit{一个GydF4y2Ba}$，找到一个预处理器可能不那么简单。GydF4y2Ba

有关如何通过线性系统来近似微分方程，并利用具有多网格预分布式迭代求解器解决它的一个示例，请参见GydF4y2Ba解微分方程使用多网格预分布式离散GydF4y2Ba。GydF4y2Ba