高斯消去法和部分旋转
在极少数情况下,高斯消元法与部分旋转是不稳定的。但情况是我们不太可能继续使用算法作为矩阵计算的基础。
内容
主的增长
我几乎犹豫地把这个。高斯消去法和部分旋转可能是不稳定的。我们知道一个特定的测试矩阵,并知道它多年来,在解决线性方程组计算我们的标志性的反斜杠符是比我们通常认为的不准确。受到污染的解决方案是让人难以接受大舍入误差与消除过程中遇到较大的元素。的矩阵是由以下功能,它的一个特例gfpp函数在尼克•海厄姆的MATLAB测试矩阵的集合。
类型gfpp
函数= gfpp (n) % = gfpp (n)主的增长部分旋转。=眼(n, n) -下三角阵((n, n), 1);(:,n) = 1;
这是8-by-8。
n = 8 = gfpp (n)
n = 8 A = 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
高斯消去法和部分旋转不做任何与这个特定的旋转矩阵。第一行是添加到每个其他的行介绍第一列中的零。这在最后一列生产2。当类似的步骤重复创建一个上三角U在最后一列元素和每一步的两倍。生长在最后三角因子的元素U是2 ^ (n - 1)。
陆[L U] =(一个);U
U = 1 0 0 0 0 0 0 1 0 1 0 0 0 0 0 2 0 0 1 0 0 0 0 4 0 0 0 1 0 0 0 8 0 0 0 0 1 0 0 16 0 0 0 0 0 1 0 32 0 0 0 0 0 0 1 64 0 0 0 0 0 0 0 128
如果矩阵的顺序n将浮点词的的比特数(+ 1),最后对角元素U将增长1 /每股收益。
n = 53 = gfpp (n);陆[L U] =(一个);unn = U (n, n)
n = 53 unn = 4.5036 e + 15
如果我们试图使用反斜杠来解决线性系统涉及这个矩阵和一个随机的右手边,后面的替换将开始U (n, n)。舍入误差可以将一样大每股收益(U (n, n))和沼泽的解决方案本身。
b = randn (n, 1);x = \ b;
通常,我们希望解决方案计算高斯消去法有残余的舍入误差。但在这种情况下,许多数量级较大的残余。反斜杠已经失败了。
r = b - x *;relative_residual =规范(r) /(规范(A) *规范(x))
relative_residual = 3.7579 e-05
交换行
任何我们做的这个矩阵在消除引发旋转将防止元素的增长U。一种可能性是交换的前两行。
一个= gfpp (n);((1 2):)= ((2 - 1):);陆[L U] =(一个);unn = U (n, n)
unn = 2
这是更好的。现在使用反斜杠看看剩余。
x = \ b;r = b - x *;relative_residual =规范(r) /(规范(A) *规范(x))
relative_residual = 1.7761 e-17
所以现在剩余的舍入相对一个和x。反斜杠是否按预期运行。
引入噪声
引发旋转的另一种方法是扰乱矩阵与白噪声。
一个= gfpp (n);一个= A + randn (n, n);陆[L U] =(一个);unn = U (n, n)
unn = -3.8699
所以U表现得很好。让我们看看关于反斜杠。
x = \ b;r = b - x *;relative_residual =规范(r) /(规范(A) *规范(x))
relative_residual = 1.2870 e-16
再剩余的舍入的订单,反斜杠是否按预期运行。
生长因子
假设我们使用高斯消去法与任何旋转过程解决涉及矩阵的线性方程组美元美元。让美元现代{i, j} ^ {(k)} $表示矩阵中的元素k美元后一步的消除。的生长因子旋转过程的数量
$ $ \ρ= {\ max_ {i, j, k} |现代{i, j} ^ {(k)} | \ / \ max_ {i, j} |现代{i, j} |} $ $
这种生长因子数量威尔金森的舍入误差分析至关重要。如果\ρ美元不是太大,然后消除算法是稳定的。不幸的是,这个矩阵我们刚刚看到的,gfpp表明,生长因子的局部旋转至少2美元^ {n} $。
当时他提出他的分析在1970年代早期,威尔金森知道这个矩阵。但他说,这是一个非常特殊的情况。他说:
我们的经验是,任何连续大幅增加的元素的大小是非常罕见的即使有部分旋转……没有例子,自然出现了在我的经验增加16一样大。
LINPACK的开发过程中在1970年代末,一个同事在阿贡,j·t·古德曼,用随机矩阵和我做了一些实验来检查元素增长与部分旋转。我们使用不同的元素分布和矩阵的温和秩序,即$ n的值有10至50美元。我们发现的最大生长因子是一个矩阵的0和1的订单40。价值\ρ= 23美元。我们从未看见一样大的线性增长,美元$ \ρ= n,更不用说指数,美元\ρ= 2 ^ {n} $。
平均情况下增长
尼克Trefethen和罗伯·施赖伯发表了一篇重要的文章,“平均情况稳定高斯消去法”,在1990年。他们提出了两种理论和概率模型,并且广泛的实验的结果。他们表明,许多不同类型的矩阵,典型的生长因子偏旋转不会增加指数矩阵n美元。它甚至不线性增长。它实际上变得像$ n ^ {2/3} $。最后一节中,“结论”,开始:
高斯消去法和局部平均旋转稳定吗?一切我们知道在这个问题上着重表明答案是是的,,不需要假设之外的统计特性来解释这个算法的成功在近半个世纪的数字计算。
坏的情况下成长
海厄姆兄弟,尼克和Des海厄姆,1989年发表了一篇论文高斯消去法的生长因子。大多数纸适用于任何类型的旋转和涉及增长这是O (n)美元。但他们确实有一个定理只适用于部分旋转和矩阵描述所有美元\ρ= 2 ^ {n} $。本质上这些矩阵必须有行为我们已经看到gfpp,即没有实际旋转和每一步添加一行以后的所有行,最后一列中的值翻倍。
指数增长在实践中
在两个不同的文件,斯蒂芬·赖特在1993年和莱斯福斯特1994年,作者展示了类的矩阵计算实践中遇到的高斯消元法与部分旋转吹了指数级增长的最后几列的元素U。赖特的应用程序是一个常微分方程的两点边值问题。离散近似产生一个乐队矩阵。福斯特的应用程序是一个种群动态沃尔泰拉积分方程模型。离散近似产生较低的梯形矩阵。在这两种情况下,矩阵是增强了最后一列。某些参数的选择原因消除继续没有旋转,导致指数增长在最后一列。类似的行为gfpp海厄姆定理和最坏的情况下增长。
完整的旋转
完整的旋转需要O (n ^ 3)美元的比较,而不是O (n ^ 2)所需的美元部分旋转。更重要的是,重复访问整个矩阵完全改变了内存访问模式。随着现代计算机存储层次结构,包括缓存和虚拟内存,这是一个重要的考虑因素。
生长因子\ρ与美元完成旋转是有趣的,我计划在我的下一个调查的博客。
lugui
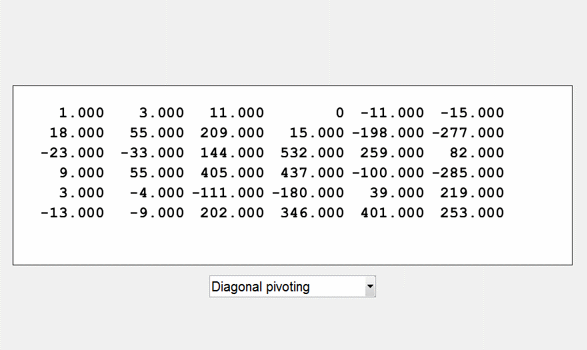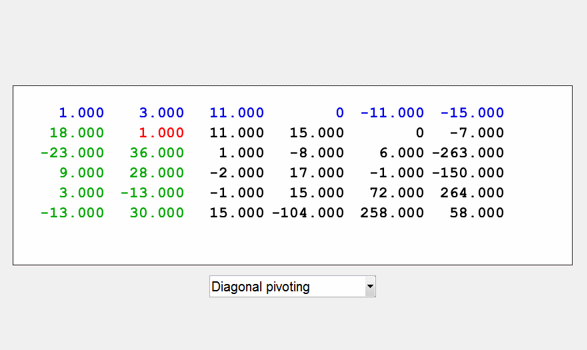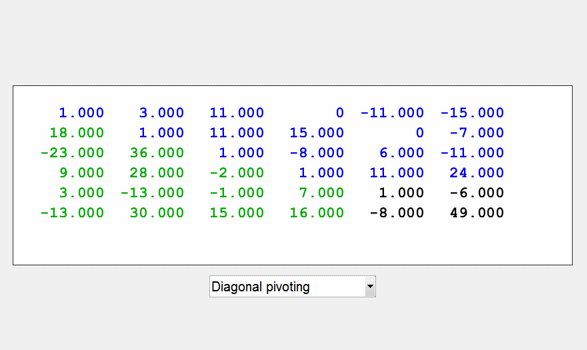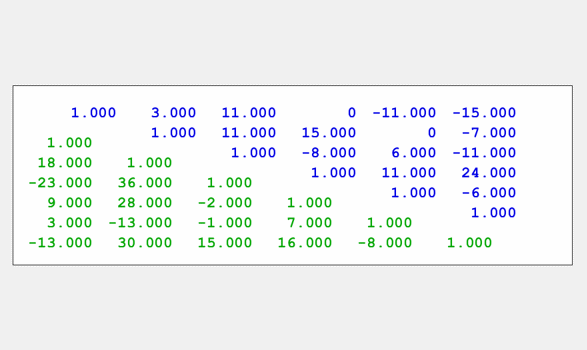
lugui附带的示范项目之一与MATLAB数值计算。我也会在我的下一篇博客中描述它。现在,我只会用它来为这个博客生成图形。这是分解的结果,下三角的因素l在绿色和上三角的因素U蓝色的。
一个= gfpp (6);lugui (,“部分”)

引用
尼古拉斯·j·海厄姆和德斯蒙德·j·海厄姆“大型生长因子与旋转高斯消去法”,< http://www.maths.manchester.ac.uk/ ~海厄姆/论文/ hihi89.pdf>,暹罗j .矩阵肛门。达成。155 - 164年,1989年。
劳埃德·n . Trefethen和罗伯特·s·施赖伯高斯消去法的平均情况稳定,暹罗j .矩阵肛门。335 - 360年达成。11日,1990年。
斯蒂芬·j·赖特的集合问题的高斯“消除部分旋转不稳定”,< ftp://info.mcs.anl.gov/pub/tech_reports/reports/P266.ps.Z>,暹罗j .科学。中央集权。231 - 238年第一版。14日,1993年。
莱斯利·福斯特“高斯消去法可以在实践中失败”,< http://www.math.sjsu.edu/福斯特/ geppfail.pdf>,暹罗j .矩阵肛门。:15,1354 - 1362,1994。














 克里夫的角落:克里夫硅藻土在数学和计算
克里夫的角落:克里夫硅藻土在数学和计算 MATLAB的博客
MATLAB的博客 史蒂夫与MATLAB图像处理
史蒂夫与MATLAB图像处理 人在仿真软件万博1manbetx
人在仿真软件万博1manbetx 深度学习
深度学习 开发区域
开发区域 斯图尔特的MATLAB视频
斯图尔特的MATLAB视频 在标题后面
在标题后面 文件交换的选择
文件交换的选择 汉斯在物联网
汉斯在物联网 学生休息室
学生休息室 MATLAB社区
MATLAB社区 MATLABユーザーコミュニティー
MATLABユーザーコミュニティー 创业、加速器,和企业家
创业、加速器,和企业家 自治系统
自治系统





评论
留下你的评论,请点击在这里MathWorks账户登录或创建一个新的。