MATLAB函数对积分的数值求值是由四,通过quadl而且quadgk，到今天的积分．

内容

交

几年前，我自认为是逼近积分的数值方法方面的专家。但后来我有一段时间没再注意了。所以这是一个重新认识的机会。该任务涉及一个实变量$x$的实值函数$f(x)$，它定义在区间$a \le x \le b$上。我们试图计算定积分的值，$$ \int_a^b \ f(x) \ dx $$关于这个主题我在课本上写了一章MATLAB数值计算．这是该章节的链接．这一章的标题是“正交”。我在这一章要做的第一件事就是解释这一点交定积分是一个老式术语，源于这样一种概念，即定积分的值可以通过在图形纸上绘制函数，然后计算落在图形下面的小方块的数量来近似。这是一张粗略的图片。

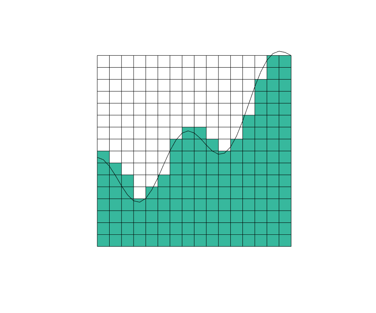
Adaptive Simpson的方法和四

从MATLAB开始的大部分时间里，直到12年前我写关于正交的那一章，求定积分的MATLAB函数被命名为四．它基于自适应辛普森方法(adaptive Simpson’s method)，由我的研究生伙伴Bill McKeeman首创，用于展示Algol中的递归。这两个图说明了自适应辛普森方法的基础。该算法在原始区间[a,b]的子区间上递归地工作。如果从3点辛普森法则和5点复合辛普森法则得到的值在指定的公差范围内一致(对于这些数字，它们显然不是)，那么从这两个值中得出的外推值被接受为子区间上的积分值。如果不是，则将算法递归应用于子区间的两半。

的线条而且quadgui

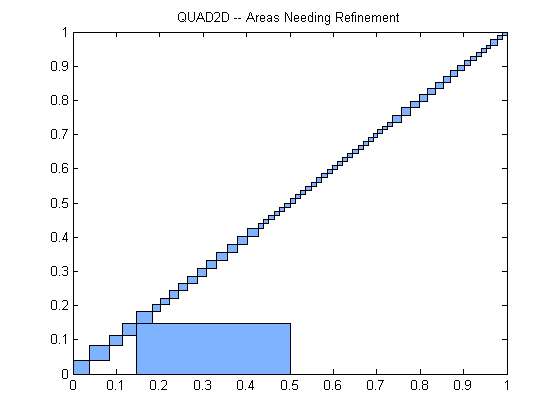
我使用了一个名为的线条来证明数值积分。它在x = 0.3处有一个强烈的峰值，在x = 0.9处有一个温和的峰值。它在MATLAB中也有应用演示目录，所以你在自己的机器上有它。如下图所示。$$ h(x) = \frac{1}{(x-0.3)^2+。01} + \frac{1}{(x-0.9)^2+。04} - 6 $$ An interactive graphical app namedquadgui是包括在程序MATLAB数值计算，可从MATLAB中央文件交换．它显示了四在行动。这是一个快照四部分通过计算的积分的线条在区间[0,1]内。在区间1/4左边的积分就完成了。在子区间[1/4,3/8]上的积分已经成功地完成了。在初始化过程中计算了3/8右侧的几个样本。被积函数求了19次。这是最终结果。的默认容差四$10^{-6}$，六位有效数字的积分值为29.8583。被积函数求了93次。大多数评估都是在峰值附近进行的的线条迅速变化。这表明自适应按预期工作。 的线条是有理函数。利用“符号工具箱”可以解析地先求不定积分，再求定积分。

信谊xh = 1 / ((x-3/10) ^ 2 + 1/100) + 1 / ((x-9/10) ^ 2 + 4/100) - 6 int I = (h, x) D =潜艇(我,1)潜艇(我,0)格式长Q = double(D)

h = 1 / ((x - 9/10) ^ 2 + 1/25) + 1 / ((x - 3/10) ^ 2 + 1/100) - 6 I = 10 * (10 * x - 3) -每股6 * x + 5 * (5 * x - 9/2)每股D = 5 *(1/2) +每股10 *:(3)+ 10 *(7)每股+ 5 *(9/2)——每股6 Q = 29.858325395498674

这证实了所显示的六位数的价值quadqui

洛巴托，克朗罗德和quadl

大约在2004年的时候，我正在写交章的不合格品,quadl函数出现了。这使用了Lobatto规则。$ $ \ int_ {1} ^ 1 \ f (x) \ dx \ \大约\ w_1 f (1) + w_2 f (-x_1) + w_2 (x_1) + w_1 f (1) $ $ $ x_1 = 1 / \√,{5}\ w_1 = 1/6 \ w_2 = 5/6美元。Quadl也使用了相关的Kronrod规则，该规则提供了13个额外的非理性横坐标和权重。Lobatto-Kronrod规则的阶数要高得多，因此比辛普森规则更准确。结果是quadl通常比?更快更准确四．但我在书中只做了几个练习quadl．我认为它从来没有变得很受欢迎。

高斯，克朗罗德，还有quadgk

在数学软件业务中，当我们使用Fortran或C开发库时，我们通过计算函数求值的次数来评估数值求积的成本。2006年，新加坡管理大学教授Larry Shampine，他是MathWorks的顾问，也是我们ODE Suite的主要作者，发表了下面引用的论文，他在MATLAB环境中改变了正交函数的基本规则。由于MATLAB函数求值是向量化的，我们应该计算向量化求值的个数，而不是单个求值的个数。这可以更好地预测执行时间。Shampine的论文中包含了一个他调用的MATLAB函数quadva,在那里弗吉尼亚州代表“向量化自适应”。他的代码使用15点高斯-克朗罗德公式。高斯公式不仅在点数相同的情况下比Lobatto公式高阶，它还有一个额外的优点，那就是它不需要在区间的端点处计算被积函数。这使得在端点处处理无限区间和奇点成为可能。当我们加入香波的时候quadva到MATLAB，我们称之为quadgk，表示“高斯-克朗罗德”。

比较的线条．

我们仪器的线条在一个简单的测试用例上研究我们的正交例程的行为。的函数四而且quadl使用vector参数调用被积函数一次以初始化积分，然后在自适应过程中使用较短的vector参数调用多次。这是一个如此简单的问题quadgk获取初始化期间所需的所有信息。在下表中，“init”是初始化调用中向量的长度，“kount”是初始化调用的次数的线条初始化后调用，“length”是这些调用中vector参数的长度，“err”是最终结果中的错误，“time”是执行时间(以毫秒为单位)。$$\begin{array}{lrrrrr} & \mbox{init} & \mbox{kount} & \mbox{length} & \mbox{err\ \\ \} & \mbox{quad} & 7 & 69 & 2 & 7.3 \cdot 10^{-7} & 0.87 \\ \mbox{quadl} & 13 & 37 & 5 & 1.8 \cdot 10^{-10} & 0.78 \\ \mbox{quadgk} & 150 & 0 & - & 2.5 \cdot 10^{-14} & 0.34 \end{array}$$我们看到这三个函数在这个实验中的表现非常不同。最古老的函数，四，实际上需要最少的总函数计算，如果我们在传统的标量意义上计算它们，但它是最不准确和最慢的。最新的函数，quadgk，只需要一次向量化函数求值，是最快和最准确的。

quadgk就变成了积分

在2012年，随着2012a版本的发布，我们意识到大多数想要计算积分的MATLAB新用户都很难找到名为“quadgk”的函数来完成这项工作。这些年来，我们这些数字分析师一直在向世界其他地方解释我们这个古怪的术语交．如果这还不够，我们还得加上数学家名字的首字母。我们介绍了积分．实际上quadgk仍然可用。积分只是一个更容易找到和更容易使用的版本quadgk．

参考

L.F. Shampine， "矢量化自适应正交的MATLAB，计算与应用数学杂志211(2006)，第131 - 140页，载于< http://faculty.smu.edu/shampine/rev2vadapt.pdf>

获取MATLAB代码发布与MATLAB®R2016a