ode15i
求解全隐式微分方程-变阶法
语法
描述
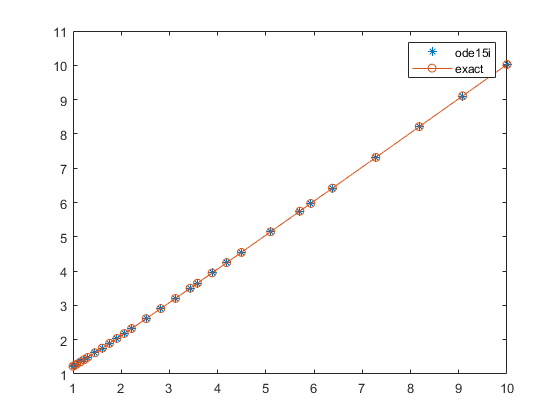
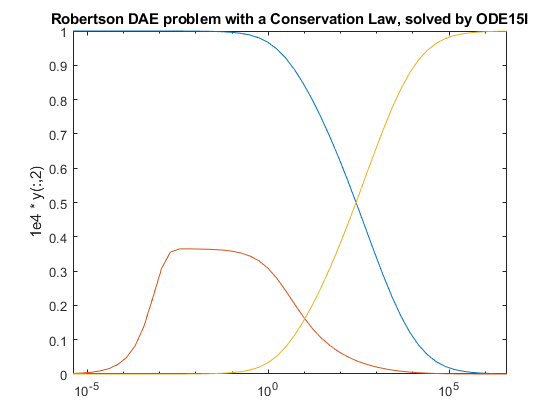
例子
输入参数
输出参数
提示
提供了雅可比矩阵
ode15i是可靠性和效率的关键。或者,如果系统是大的和稀疏的,那么提供雅可比矩阵稀疏模式也帮助求解者。在任何情况下,使用odeset方法传入矩阵雅可比矩阵要么JPattern选项。
算法
ode15i是一种基于1 ~ 5阶反向微分公式(BDFs)的变步变序(VSVO)求解器。ode15i被设计用于全隐式微分方程和指数-1微分代数方程(DAEs)。辅助函数decic计算适于与其一起使用一致的初始条件ode15i[1]。
参考文献
[1]劳伦斯F. Shampine,“解决0 = F(T,Y(t)的,Y'(t))的在MATLAB,”杂志数值数学,10卷,第4期,2002年,第291-310。