典型的优化问题

这个例子展示了如何使用基于问题的方法来解决一个约束非线性优化问题。该示例演示了典型的工作流程:创建目标函数、创建约束、解决问题，并检查结果。

注意:

如果你的目标函数或非线性约束不是由初等函数组成的，你必须将非线性函数转换为最优化表达式fcn2optimexpr．请参阅本示例的最后一部分，使用fcn2optimexpr替代配方,或将非线性函数转换为优化表达式．

关于这个问题的基于求解器的方法，请参见求解一个约束非线性问题，基于求解器．

问题公式化:罗森布罗克函数

考虑最小化罗森布罗克函数的问题

在单位圆，即圆心为原点，半径为1的圆盘。换句话说，就是找到 $$x$$使函数最小化 $$f（x）$$在一组 $$x_1^2+x_2^2\le 1$$．这个问题是受非线性约束的非线性函数的极小化问题。

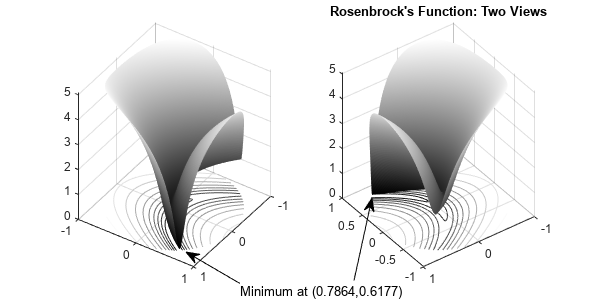
罗森布罗克函数是优化中的一个标准测试函数。它在这一点有一个唯一的最小值0[1]．寻找最小值对于某些算法来说是一个挑战，因为函数在一个深弯曲的山谷中有一个浅的最小值。这个问题的解决办法还没有到关键的时候[1]因为这个点不满足约束条件。

该图显示了Rosenbrock在单位磁盘中的功能的两个视图。纵轴为对数比例;换句话说，情节显示 $$\mathrm{日志}（1+f（x））$$．等高线在平面图下面。

Rosenbrock = @(x)100*(x(:，2) - x(:，1).^2)。^2 + (1 - x(:，1))%矢量化函数图1 =图(“位置”，[1 200 600 300]);colormap (“灰色”）;轴广场；R = 0: .002:1;TH = 2 *π* (0:.002:1);X = R ' * cos (TH);Y = R ' * sin (TH);Z = log(1 + rosenbrock([X(:)，Y(:)])));Z =重塑(Z,大小(X));%创建次要情节subplot1 =次要情节(1、2、1,“父”,图1);视图([124 34]);网格(“上”）;持有在；%建立表面冲浪(X, Y, Z,“父”subplot1,“线型”，“没有”）;%创建轮廓轮廓(X, Y, Z,“父”, subplot1);%创建次要情节subplot2 =次要情节(1、2、2、“父”,图1);视图([234 34]);网格(“上”）;持有在%建立表面冲浪(X, Y, Z,“父”subplot2,“线型”，“没有”）;%创建轮廓轮廓(X, Y, Z,“父”, subplot2);%创建textarrow注释(图1,“textarrow”(0.4 - 0.31),．..(0.055 - 0.16),．..“字符串”, {的最低(0.7864,0.6177)})；%创建箭头注释(图1,“箭头”(0.59 - 0.62),．..[0.065 - 0.34]);标题(“罗森布罗克的功能:两种观点”)举行从

的。函数句柄在任意数量的二维点上计算Rosenbrock函数。这向量化加快了函数的绘图速度，并且在其他环境中可以用于在多个点上加快函数的计算速度。

这个函数 $$f（x）$$被称为目标函数。目标函数就是你想要最小化的函数。的不平等 $$x_1^2+x_2^2\le 1$$被称为约束。约束限制的集合 $$x$$求解器在上面寻找最小值。你可以有任意数量的约束条件，也就是不等式或方程。

使用优化变量定义问题

基于问题的优化方法使用优化变量来定义目标和约束。有两种方法可以使用这些变量创建表达式:

对于这个问题，目标函数和非线性约束都是多项式，所以可以直接用优化变量的形式来表示。创建一个2-D优化变量“x”．

x = optimvar (“x”、1、2);

在优化变量中创建一个多项式的目标函数。

= 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;

创建一个名为概率有obj作为目标函数。

概率= optimproblem (“目标”、obj);

在优化变量中创建一个多项式的非线性约束。

Nlcons = x(1)^2 + x(2)^2 <= 1;

在问题中包含非线性约束。

prob.Constraints.circlecons = nlcons;

回顾这个问题。

显示(概率)

优化问题:求x最小化:((100 .* (x(2) - x(1).^2).^2) + (1 - x(1)).^2)服从圆:(x(1).^2。^2 + x(2) ^2 <= 1

解决问题

为了解决优化问题，调用解决．问题需要一个初始点，初始点是一个给出优化变量初值的结构。创建初始点结构x0拥有一个 $$x$$价值的[0 0]．

x0。x＝[0 0]；[溶胶,fval exitflag、输出]=解决(x0概率)

使用fmincon解决问题。找到满足约束条件的局部最小值。优化完成是因为目标函数在可行方向上不减小到最优性公差的值内，约束条件满足到约束公差的值内。

索尔=结构体字段:x (0.7864 - 0.6177):

fval = 0.0457

exitflag = OptimalSolution

输出=结构体字段:第一个迭代:24 funcCount: 34 construct: 0 stepsize: 6.9161e-06 algorithm: ' internal -point' firstderopt: 2.1625e-08 cgiterations: 4 message: '…* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *

检查解决方案

解决方案展示exitflag = OptimalSolution．此退出标志表明该解决方案是局部最优的。有关尝试找到更好的解决方案的信息，请参见当求解成功时．

退出消息表明解决方案满足约束条件。您可以用几种方法检查解决方案是否确实可行。

infeas = output.constrviolation

infeas = 0

0的不可行性表明解是可行的。

infeas =不可行性(nlcons sol)

infeas = 0

同样，0的不可行性表明解是可行的。

nx =规范(sol.x)

nx = 1.0000

的输出结构提供了关于解决过程的更多信息，例如迭代次数(24次)、求解器(fmincon)，函数求值次数(84)。有关这些统计信息的更多信息，请参见公差和停止标准．

替代配方使用fcn2optimexpr

对于更复杂的表达式，为目标函数或约束函数编写函数文件，并使用fcn2optimexpr．例如，非线性约束函数的基在disk.m文件:

类型磁盘

函数radsqr = disk(x) + x(2)^2;

将此函数文件转换为优化表达式。

radsqexpr = fcn2optimexpr (@disk x);

此外，您还可以转换。在绘图例程开始时定义的函数句柄，转换为优化表达式。

rosenexpr = fcn2optimexpr(。,x);

使用这些转换后的优化表达式创建优化问题。

convprob = optimproblem (“目标”rosenexpr,“约束”radsqexpr < = 1);

查看新问题。

显示(convprob)

优化问题:解:x最小化:anonymousFunction2(x) where: anonymousFunction2 = @(x)100*(x(:，2)-x(:，1).^2).^2+(1-x(:，1)).^2;Subject to: disk(x) <= 1

解决新问题。解决方案基本上和之前一样。

[溶胶,fval exitflag、输出]=解决(x0 convprob)

使用fmincon解决问题。找到满足约束条件的局部最小值。优化完成是因为目标函数在可行方向上不减小到最优性公差的值内，约束条件满足到约束公差的值内。

索尔=结构体字段:x (0.7864 - 0.6177):

fval = 0.0457

exitflag = OptimalSolution

输出=结构体字段:第一个迭代:24 funcCount: 84 construct: 0 stepsize: 6.9162 -06 algorithm: ' internal -point' firstderopt: 2.4373e-08 cgiterations: 4 message: '…最佳可行:[1x1 struct] objective - derivative:“有限差分”constraint - derivative:“有限差分”solver:“fmincon”

有关支持的函数列表，请参见万博1manbetx万博1manbetx支持优化变量和表达式的操作．