Kuramoto振荡器的稳定性
我使用Indika Rajapakse和史蒂夫·斯梅尔调查描述Kuramoto振子的动态系统的稳定性。Indika和史蒂夫感兴趣Kuramoto振荡器有两个原因;自同步提供了一个模型的细胞在跳动的心脏和动态系统是Morse-Smale理论的一个例子。我个人感兴趣的Kuramoto模型相关脑深部电刺激(DBS)开环控制的人类运动障碍。我的kuramoto程序演示了稳定和不稳定的临界点。舍入误差可能会破坏一个不稳定的临界点。
内容
潜在的
n美元Kuramoto模型是一个系统的常微分方程描述的时间进化,美元\ theta_k美元(t),振动组件。我们的分析的关键是表达方程势函数的梯度,
$ $ v (t) = \压裂{4}{n ^ 2} \ sum_k {\ sum_ {j > k}{\罪^ 2{\压裂{\ theta_j (t) - \ theta_k (t)} {2}}}} $ $
4美元/ n ^ 2美元可实现潜在的这样
le v $ $ 0 \ \ 1 $ $
当所有的美元\ theta_k (t)是相等的,美元的振荡器是完全同步和v (t) = 0美元。另一方面,如果美元\ theta_k (t)是等距的美元在整个区间[0,2π\],美元的振荡器不同步和v(1) = 1美元。
五美元的梯度,写$ \微分算符v $,是向量的分量是偏导数,
$ $ \压裂{\部分v}{\部分\ theta_k} = - \压裂{2}{n ^ 2} \ sum_j{\罪{(\ theta_j - \ theta_k)}} $ $
一个临界点任何潜在的梯度为零。
Kuramoto模型
Kuramoto传统形式的方程
$ $ \压裂{d \ theta_k} {dt} = \ omega_k + \压裂{\ kappa} {n} \ sum_j{\罪{(\ theta_j - \ theta_k)}}, \ k = 1,…, n $ $
这里\ omega_k美元是一个常数,k th美元的固有频率振荡器,和\ kappa美元的耦合系数是非线性同步。写的潜力,成为Kuramoto向量形式的方程
$ $ \压裂{d \θ}{dt} = \ω- \压裂{\ kappa n} {2} \ v微分算符(\θ)$ $
参数的顺序
一个振荡器\ theta_k美元往往是与单位圆上的点$ e ^{我\ theta_k} $。认为这是振荡器的改变自我。
的一般振荡器,被定义为\ psi美元
$ $ | z | e ^{我\ psi} = \压裂{1}{n} \ sum_k e ^{我\ theta_k} $ $
z | |提供了另一种衡量美元级的同步命令参数。与频率旋转参考系\ psi美元经常方便。
当\ theta_k美元上等距的初始化(0,2 \π)美元,他们的平均应该是零,所以z | |应该零美元\ psi美元并不是唯一地定义。但在实践中,有限精度算法,π并不完全等于\π和美元最初\ theta_k并不完全等距的美元。即使他们,会有舍入误差计算的平均水平。因此,计算z | |不是零,美元计算ψ可以在几乎任何价值和旋转参考系可能表现不正常。
潜力和订单参数提供补充措施的同步性;当其中一个等于零等于1。我们想知道两者之间的定量关系。
kuramoto.m
我的程序kuramoto让你尝试Kuramoto的模型。关键参数的同步卡巴和固有频率的传播β。五个单选按钮标签预设对应这五本博客文章的其余部分中描述的情况。
kappa = 0,β= 0
这个例子说明了舍入误差对仿真的影响。与β等于零,所有的固有频率都等于1。和卡巴等于零,不存在同步。动力系统是简单
$ $ \压裂{d \ theta_k (t)} {dt} = 1, \ k = 1,…, n $ $
美元的初始条件,分配\ theta_k(0)的时间间隔内平均美元[0,2π\]美元,
$ $ \ theta_k(0) = \压裂{2 k \π}{n} $ $
那么,确切的解决方案
$ $ \ theta_k (t) = t + \压裂{2 k \π}{n} \ k = 1,…, n $ $
这是一个不稳定的临界点。美元\ theta_k (t)将保持等距的美元(0,2 \π)和改变自我美元e ^{我\ theta_k (t)} $将均匀分布在单位圆,除非扰乱他们的东西。
但是,因为我们是预测系统没有这样简洁的解决方案,我们使用古老的MATLAB ode求解器进行求解万博 尤文图斯数值为了计算数值解。万博 尤文图斯这可能引入了扰动的自由裁量权数值方法的误差和舍入误差的有限精度算法。让我们看看结果gif动画。仔细看。

你注意到小晃动起来吗?小精灵在工作吗?他们是无害的,但是很有趣。我还没挖到的细节数值。它是集成一个常数,所以不应该有任何离散误差。但仍存在舍入误差。
考虑一个简单的替身——欧拉方法。有一个固定的步长h。有常数向量
ω= 1 (n, 1)
微分方程非常简单;导数不依赖t或θ。
f (t,θ=ω
初始值
theta0 = (1: n) / n * 2 *π
t = 0
θ= theta0
欧拉只会积累标量时间
t = t + h
和向量解决方案
θ=θ+ h *ω
会有舍入误差,提供h两个不是一个逆功率,但就像我们的老朋友吗0.1。
这是实际的观察与错误kuramoto使用数值。确切的解决方案
θ= = t + theta0
我已经出了相对误差在单位的每股收益(θ),一个单一的舍入误差的计算解决方案。
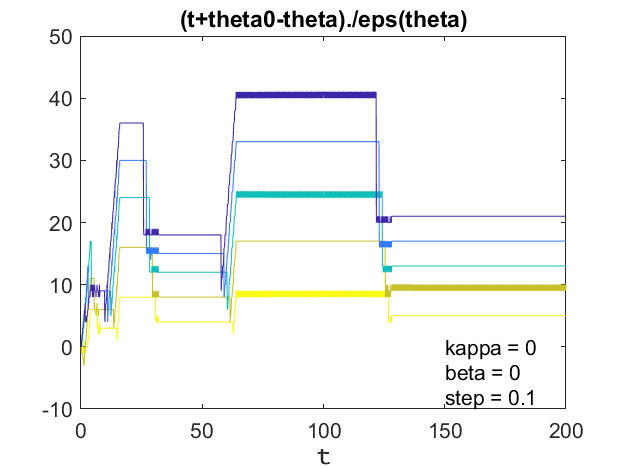
有行动时t经过2的幂- 8,16日,32岁,64年,128年。它会永远这样。临时脉冲数十舍入误差。回顾gif动画。它晃动起来的时候t2的幂。
舍入误差很少是重要的常微分方程的数值解。它出现在这里只是因为没有其他正在发生的事情。
kappa =综合β= 0
这是一个干净的同步的例子。欧米伽是相同的,有一种强烈的耦合系数。振荡器落入锁步和潜在迅速下降到零。
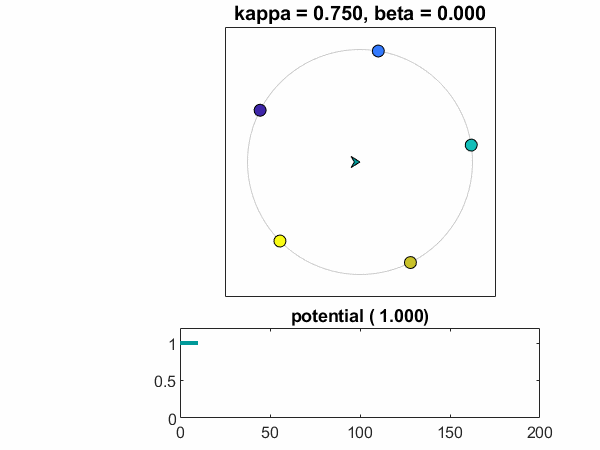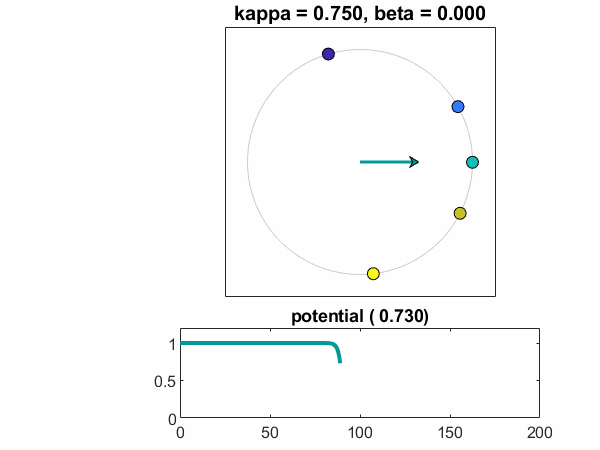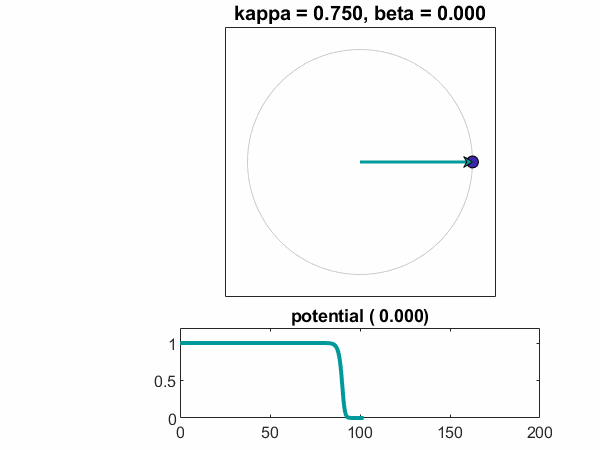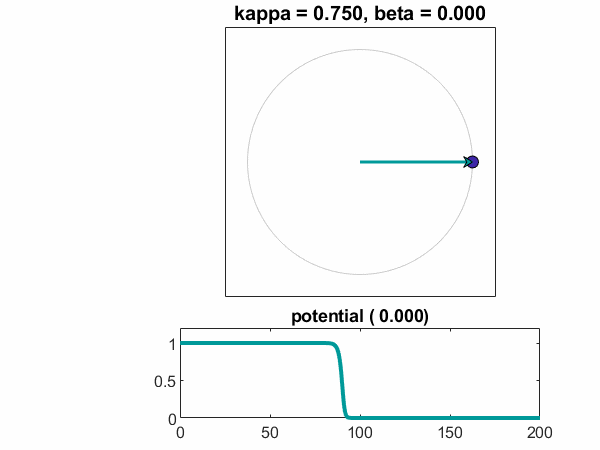
的一块θt与t显示了振荡器同意满足他们的平均值。
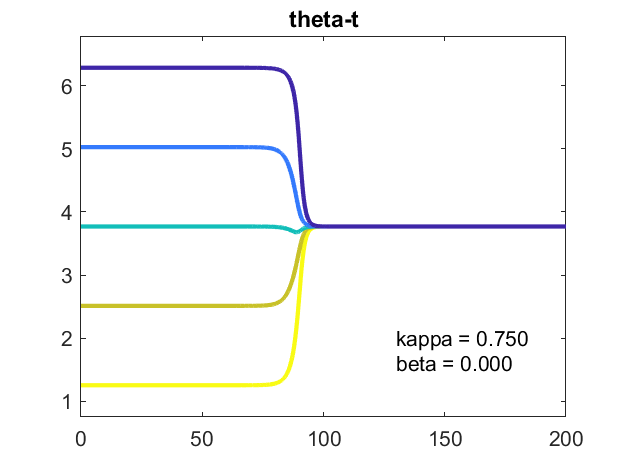
这是强度的非线性同步,潜在的梯度。
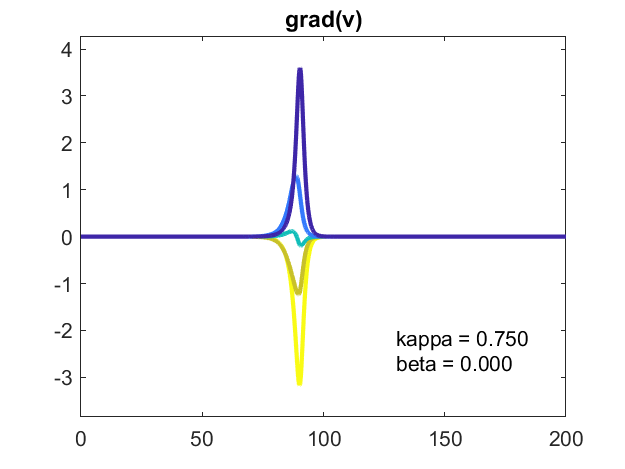
这是仔细看看研究生(v)。这是一个签署了对数图。两个组成部分研究生(v)是积极的,两个是负面的和一个彩色的蓝绿色,改变的迹象。我绘制的对数绝对值与分离轴反映了组件的迹象。大多数时候,图表的对数直线,表明相应的组件或腐烂的指数增长,开始或结束在很小的值。这些组件达到临界尺寸时,振子同步。
我还没有分析这些对数的山坡上,所以我不知道指数增长的利率或腐烂。我把这个作业。请让我知道如果你想出什么。

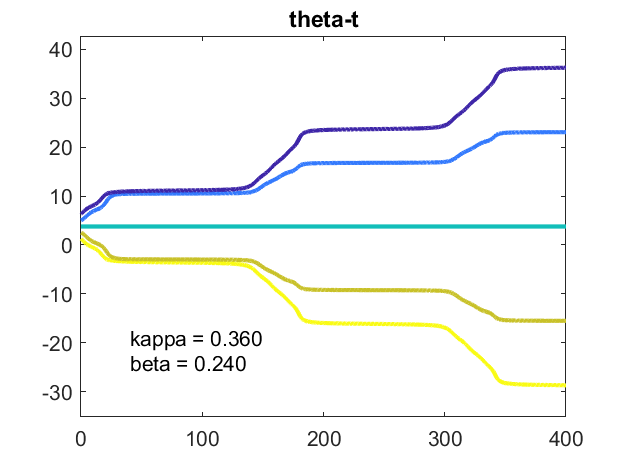
kappa = 36,β=。
其余病例在这篇文章中都有非零的值β固有频率,在向量ω不都等于1,但中均匀间隔的时间间隔(1测试版,1 +β)。在这种特殊情况下,间隔β是非线性耦合强度足够大,卡巴,不能强迫同步。振荡器几乎无法达成一个共同的频率。

当美元e ^{我\ theta_k} $是绘制在单位圆振子似乎定期方法中一种普遍的价值观。但美元的阴谋\ theta_k (t) - t与台币美元显示,它们是相互背离。单位圆运动是基于美元\ theta_k (t) 2 \ \ mbox {mod} \ \π美元。
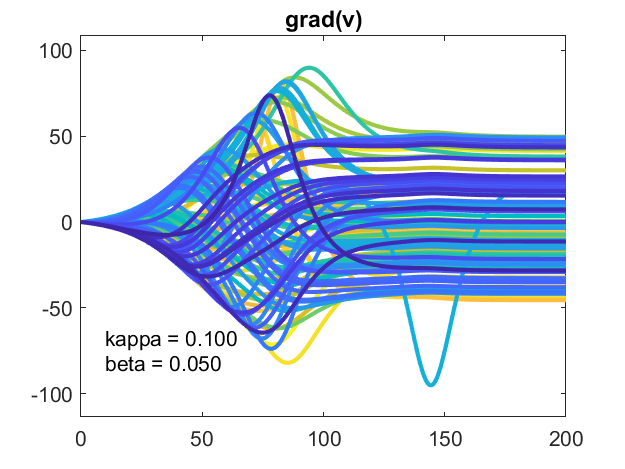
研究生(v)是很忙。
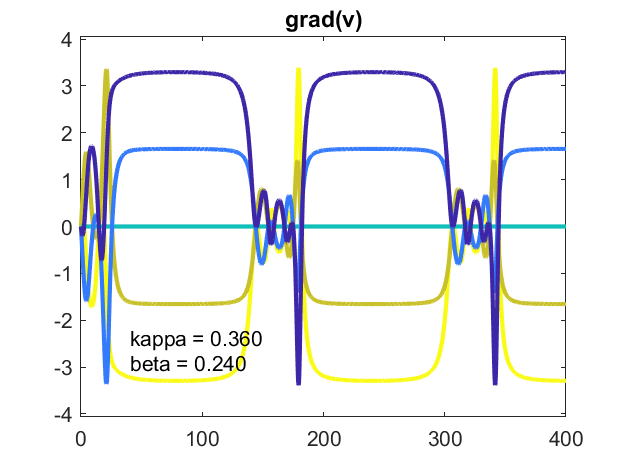
kappa = 36,β= 23)
减少固有频率的传播从一点β=。来β= 23)导致振荡器的方法,但没有达到同步。分歧保持不变,所以可能是常数,但不为零。系统是稳定的。他们是锁相。

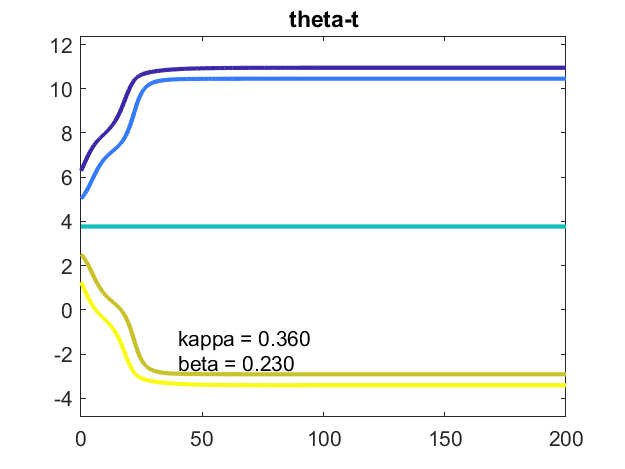
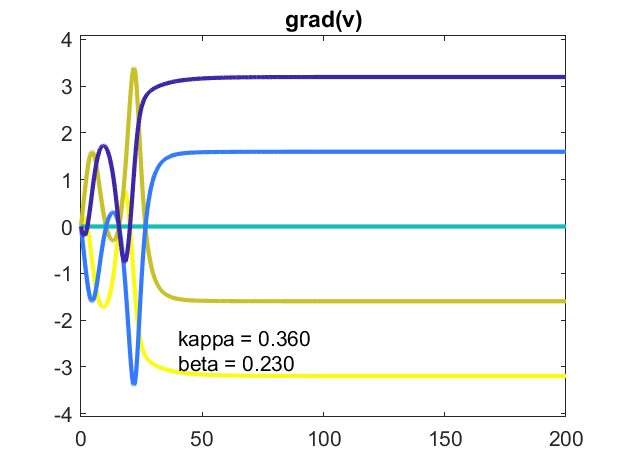
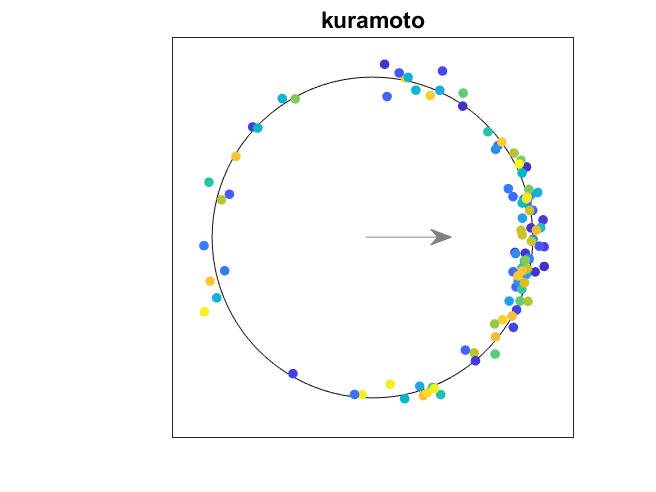
k = n = 100年,β= . 05
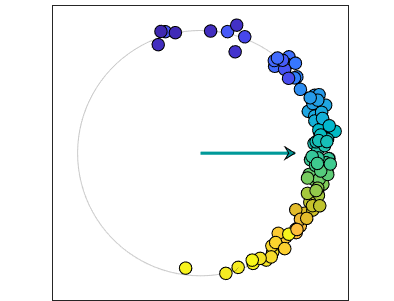
最后,让我们增加人口的规模n = 100。,第一个病例在这篇文章中,介绍一些随机性。ω从正态分布采样,集中在一个标准偏差β。随机数生成器已设置rng这样我得到同样的样本在每个运行。看一个振荡器,彩色的蓝绿色,赶上别人。振荡器的方法稳定、锁相配置。可能趋于一个常数,非零值。
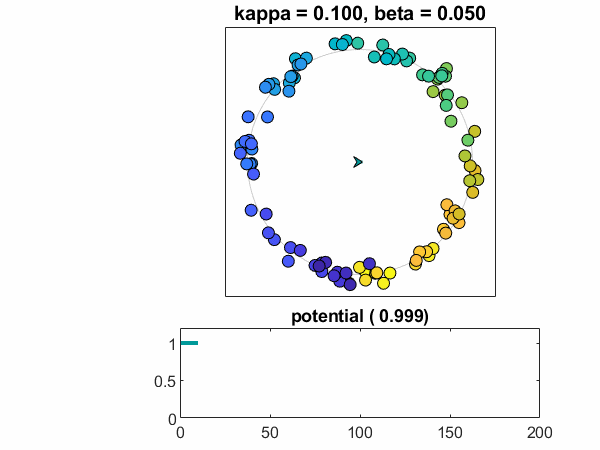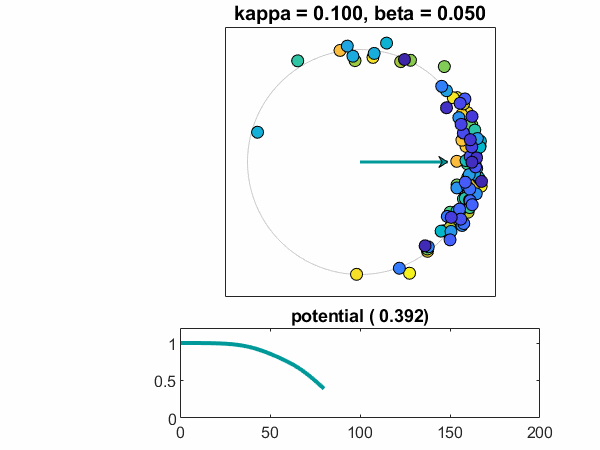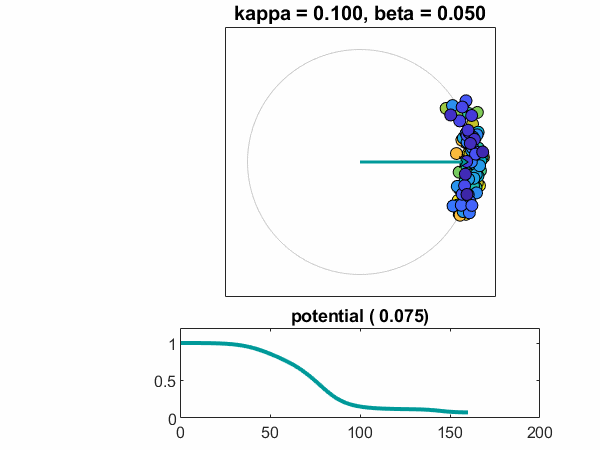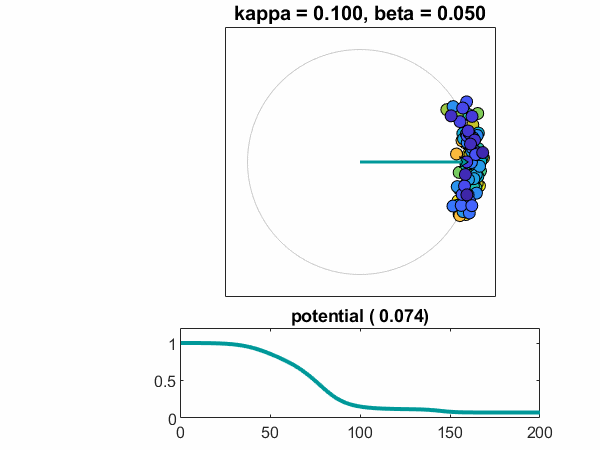
的情节θt显示了振荡器的演变分为三个稳定的团,由2 \π美元的倍数。许多快速振荡,颜色的深浅的蓝色线,形成一丛。一些缓慢的振荡器,颜色的不同深浅的黄色,形成一个缓慢的包。大多数是在一个中央组。蓝绿色的家伙比别人慢决定哪一丛加入。世界动画视图国防部2 \π,因此只能看到美元一丛。(如果我是仍然使用我们飞机彩色地图,快和慢组将红色和蓝色,唤起一个政治类比。我不去那里。)
这张照片强烈依赖于随机抽样。再次运行仿真可能产生不同的块的数量。
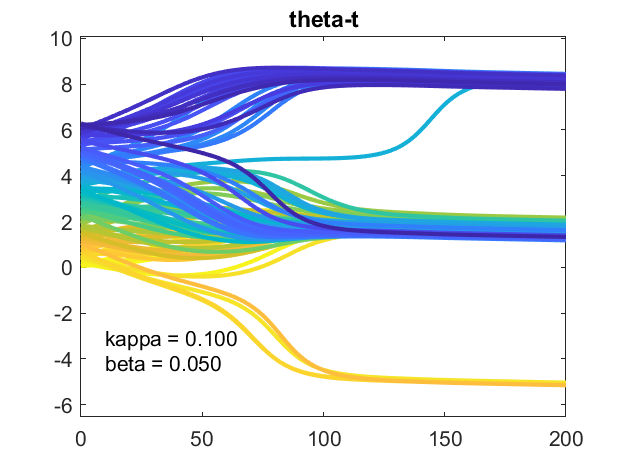
一块的梯度可能显示一个常数向量安定下来。它也暗示了结构有待探索。
软件
我有更新kuramoto在MATLAB上中央文件交换。这里是链接。我也包括克里夫的4.80版本的实验室。
链接
维基百科,Kuramoto模型,https://en.wikipedia.org/wiki/Kuramoto_model。
德克布鲁克曼和Steven strogat,“骑Kuramotocycle”,https://www.complexity-explorables.org/explorables/ride-my-kuramotocycle。
克里夫硅藻土,“Kuramoto同步振荡器模型”,https://blogs.mathworks.com/cleve/2019/08/26/kuramoto-model-of-synchronized-oscillators。
克里夫硅藻土,“与Kuramoto振荡器实验”,https://blogs.mathworks.com/cleve/2019/09/16/experiments-with-kuramoto-oscillators。
 克里夫的角落:克里夫硅藻土在数学和计算
克里夫的角落:克里夫硅藻土在数学和计算 MATLAB的博客
MATLAB的博客 史蒂夫与MATLAB图像处理
史蒂夫与MATLAB图像处理 人在仿真软件万博1manbetx
人在仿真软件万博1manbetx 人工智能
人工智能 开发区域
开发区域 斯图尔特的MATLAB视频
斯图尔特的MATLAB视频 在标题后面
在标题后面 文件交换的选择
文件交换的选择 汉斯在物联网
汉斯在物联网 学生休息室
学生休息室 MATLAB社区
MATLAB社区 MATLABユーザーコミュニティー
MATLABユーザーコミュニティー 创业、加速器,和企业家
创业、加速器,和企业家 自治系统
自治系统 定量金融学
定量金融学




评论
留下你的评论,请点击在这里MathWorks账户登录或创建一个新的。