Kuramoto振荡器的稳定性

张贴了克里尔那2019年10月30日

70次观看（过去30天）| 0.喜欢| 0评论

我正在使用Indika Rajapakse和Steve Smale来研究描述Kuramoto振荡器的动态系统的稳定性。Indika和Steve对Kuramoto振荡器感兴趣，原因有两个;自同步提供了在跳动心中的细胞模型，动态系统是莫尔斯气候理论的示例。我对Kuramoto模型个人感兴趣，因为它涉及对人类运动障碍的开环控制的深脑刺激（DBS）。我的库拉莫托程序演示了稳定和不稳定临界点。舍入误差可能使一个不稳定临界点失稳。

内容

潜力

Kuramoto模型是一个$ N $常微分方程的系统，描述了振荡组件的时间演进，$ \ theta_k（t）$。我们分析的关键是在潜在功能的梯度方面表达方程，

$$ v（t）= \ frac {4} {n ^ 2} \ sum_k {\ sum_ {j> k} {\ sin ^ 2 {\ frac {\ theta_j（t） - \ theta_k（t）} {2}}}} $$

$ 4 / n ^ 2 $正常化潜力

$$ 0 \ Le V \ Le 1 $$

当所有$ \ theta_k（t）$相等时，振荡器完全同步，$ v（t）= 0 $。另一方面，如果$ \ theta_k（t）$在整个间隔中同样间隔，则振荡器不同步，并且$ v（1）= 1 $。

$ V $的梯度，写入$ \ nabla v $，是零件是部分衍生品的矢量，

$$ \ frac {\ partial v} {\ partial \ theta_k} = - \ frac {2} {n ^ 2} \ sum_j {\ sin {（\ theta_j- \ theta_k）}} $$

一种临界点是潜在梯度为零的任何一点。

kuramoto模型

传统的Kuramoto方程式是

$$ \ frac {d \ theta_k} {dt} = \ oomega_k + \ frac {\ kappa} {n} \ sum_j {\ sin {sin {（\ theta_j- \ theta_k）}}，\ k = 1，...，$$

在这里$ \ omega_k $是一个常数，$ k $ --th振荡器的自然频率，$ \ kappa $是非线性同步术语的耦合系数。以潜力编写，克鲁莫托等式的矢量形式变成了

$$ \ frac {d \ theta} {dt} = \ oomega - \ frac {\ kappa n} {2} \ nabla v（\ theta）$$

订单参数

振荡器$ \ theta_k $通常用单位圈子$ e ^ {i \ theta_k} $的点标明。将此视为振荡器改变自我。

这平均振荡器，$ \ psi $，定义为

$$ | z | z | e ^ {i \ psi} = \ frac {1} {n} \ sum_k e ^ {i \ theta_k} $$

幅度$ | z | $提供另一种同步度量，命令参数。使用频率$ \ psi $旋转的参考帧经常方便。

当$ \ theta_k $初始化为在$ [0,2 \ pi] $同样间隔时，它们的平均值应为零，因此$ | $ | $应该为零，$ \ psi $没有唯一定义。但在实践中用有限精度算术，PI.不完全等于$ \ pi $，初始$ \ theta_k $不完全平等。即使他们是，在计算平均值时会有循环误差。结果，计算的$ | z | $不是完全零，计算Psi.可以接受几乎任何值，并且旋转参考帧可能表现不正当。

潜力和订单参数提供同步性的互补措施;当其中一个等于零时，另一个等于一个。我们想知道两者之间的数量关系。

`kuramoto.m.`

我的计划库拉莫托允许您尝试Kuramoto的模型。关键参数是同步项的强度kappa.以及内在频率的传播bet。标有五个单选按钮预设对应于本博文的其余部分中描述的五种情况。

kappa = 0，beta = 0

此示例说明了循环误差对模拟的影响。和bet等于零，所有内在频率等于1。与kappa.等于零，没有同步术语。所以动态系统简单

$$ \ frac {d \ theta_k（t）} {dt} = 1，\ k = 1，...，n $$

对于初始条件，在间隔中分发$ \ theta_k（0）$ [0,2 \ pi] $，

$$ \ theta_k（0）= \ frac {2k \ pi} {n} $$

那么，确切的解决方案是

$$ \ theta_k（t）= t + \ frac {2k \ pi} {n}，\ k = 1，...，n $$

这是一个不稳定的临界点。$ \ theta_k（t）$将保持同样超过$ [0,2 \ pi] $及其alter EGO $ e ^ {i \ theta_k（t）} $将均匀地分布在单位圈周围，除非有些东西扰乱了它们。

但是，由于我们预计没有具有这样的整洁解决方案的系统，我们使用Veneral Matlab Ode Solver万博尤文图斯ODE45.，计算数字解决方案。万博尤文图斯这可能引入了数值方法的自由判断和有限精度算术的循环误差的扰动。让我们看看这个动画GIF的结果。仔细观察。

你注意到了小摇晃吗？Gremlins在工作？它们是无害的，但有趣。我没有挖掘过细节ODE45.。它是集成的常量，因此不应该有任何离散化错误。但仍有圆形错误。

考虑更简单的拔罐的方法。有一个固定的步骤步骤尺寸H。有恒定的矢量

omega =那些（n，1）

微分方程非常简单;衍生物不依赖于任何一种T.要么θ.。

f（t，theta）= omega

初始值是

theta0 =（1：n）/ n * 2 * pi

t = 0.

Theta = theta0.

欧拉将只是积累标量时间

t = t + h

和矢量解决方案

Theta = Theta + H * Omega

提供了循环错误，提供H不是两个反力的两个，但就像我们的老朋友0.1。

这是观察到的实际错误库拉莫托使用ODE45.。确切的解决方案应该是

theta == t + theta0

我已经绘制了相对错误以单位为单位eps（θ），计算解决方案中的单个舍入误差。

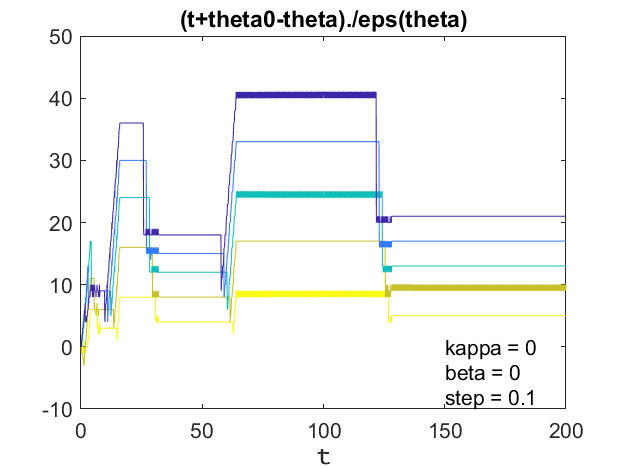
每当有行动T.通过了两到8,16,32,64,128的力量。它会永远如此。几十个舍入错误的临时脉冲。回顾动画gif。它是摇晃的时候T.通过两个力量。

循环误差在常微分方程的数值解中很少重要。它在这里出现在这里，因为没有别的事情发生了。

kappa = .75，beta = 0

这是一个干净的同步示例。所有OMEGA都相同，并且存在强烈的耦合系数。振荡器落入锁定步骤，电位迅速下降到零。

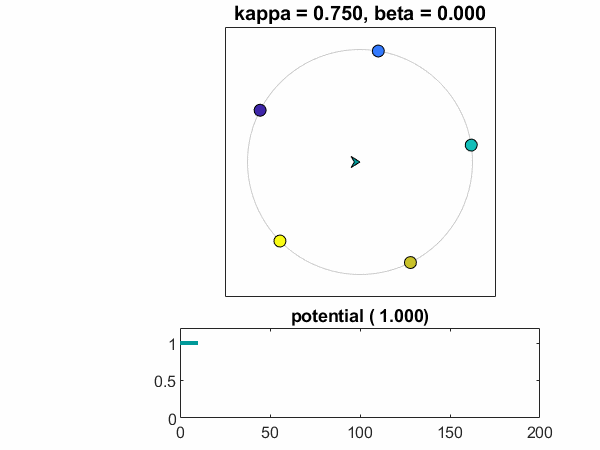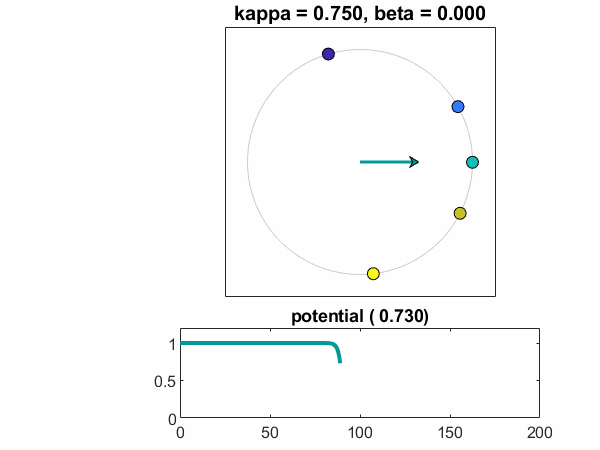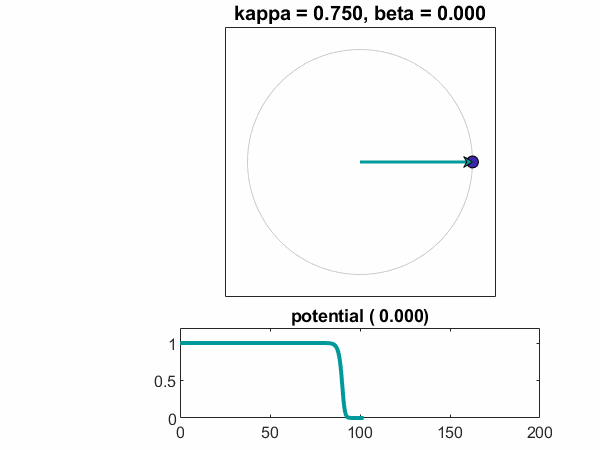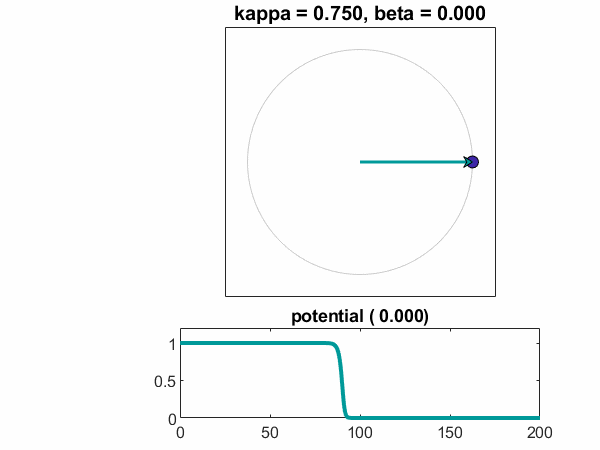
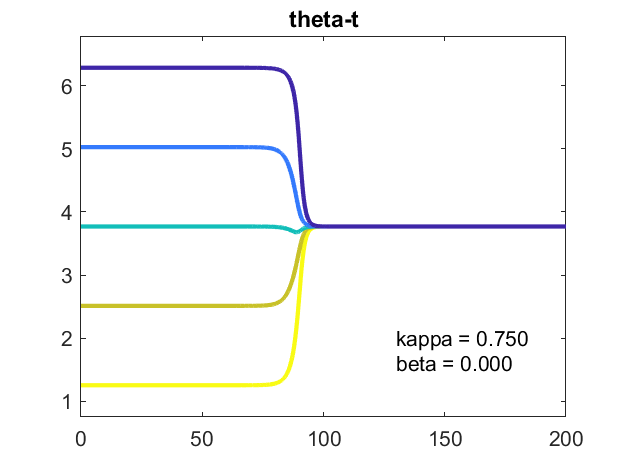
一个图Theta-T.相对T.显示振荡器同意以平均值满足。

这里是非线性同步项的强度，潜力的梯度。

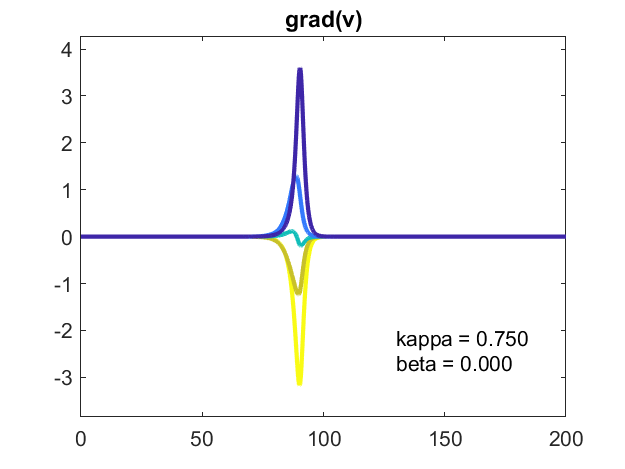
这是一个仔细的看毕业（v）。这是一个签名的对数图。两个组件毕业（v）是积极的，两个是消极的，一个，彩色的蓝绿色，变化标志。我绘制了绝对值的对数，其拆分y轴反映了组件的符号。大多数情况下，对数的图形是直线，指示相应的组件正在呈指数增长或衰减，以微小值开始或结束。当这些组件达到临界大小时，振荡器同步。

我还没有分析这些对数的斜坡，所以我不知道指数增长或腐烂的率。我会把它留给家庭作业。如果你想出任何东西，请告诉我。

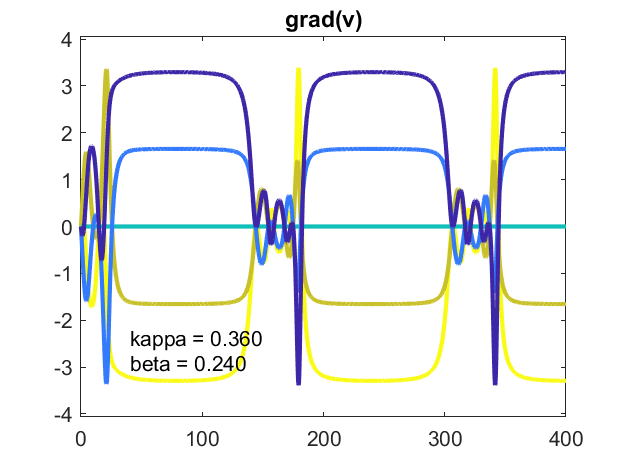
kappa = .36，beta = .24

这篇文章中的其余情况所有都有非零值bet，所以内在频率，在向量中欧米茄，并不等于一个，但在间隔中均匀间隔[1-beta，1 + beta]。在这种特殊情况下，间距bet足够大的是非线性耦合强度，kappa.，不能强制同步。振荡器几乎无法达成普通频率。

当$ e ^ {i \ theta_k} $围绕单位圆圈绘制，振荡器似乎定期接近共同值。但是，$ \ theta_k（t）-t $与$ $的情节显示它们彼此分歧。单位圆圈运动基于$ \ theta_k（t）\ \ mbox {mod} \ 2 \ pi $。

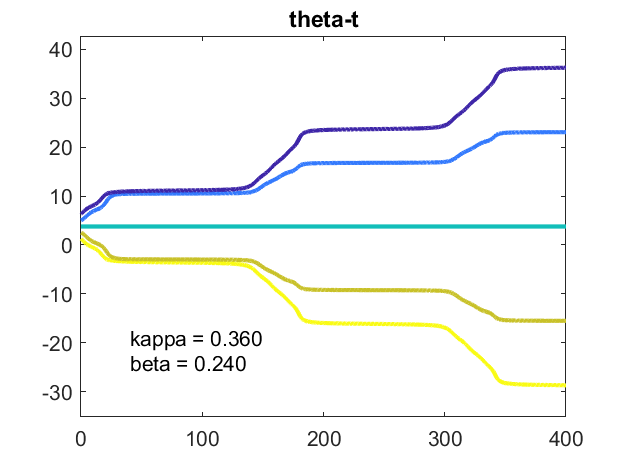
毕业（v）是很忙。

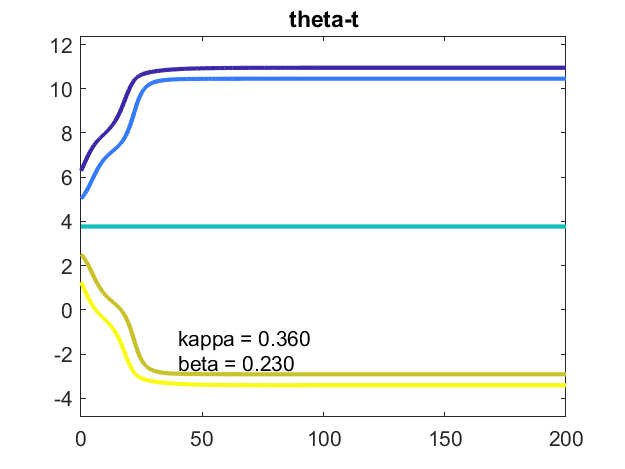
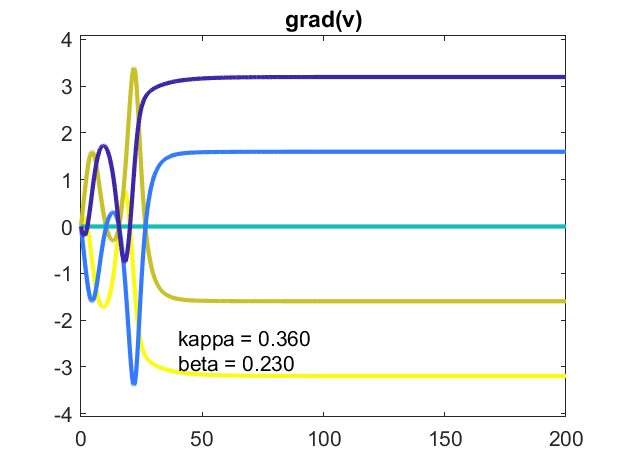
kappa = .36，beta = .23

从中减少内在频率的传播Beta = .24到beta = .23使振荡器接近，但未达到同步性。它们的差异保持不变，因此潜力是恒定的，但不是零。系统是稳定的。他们是阶段锁定。

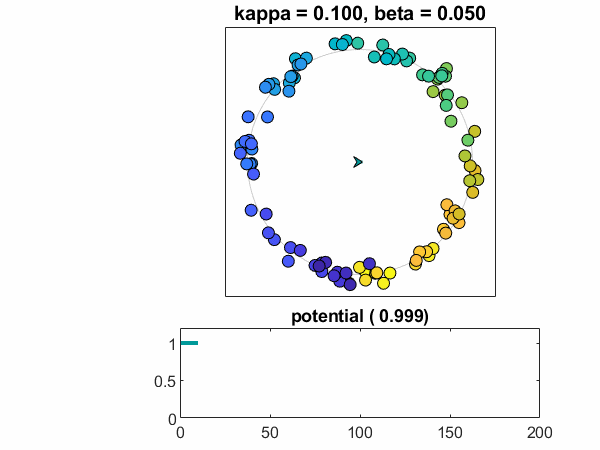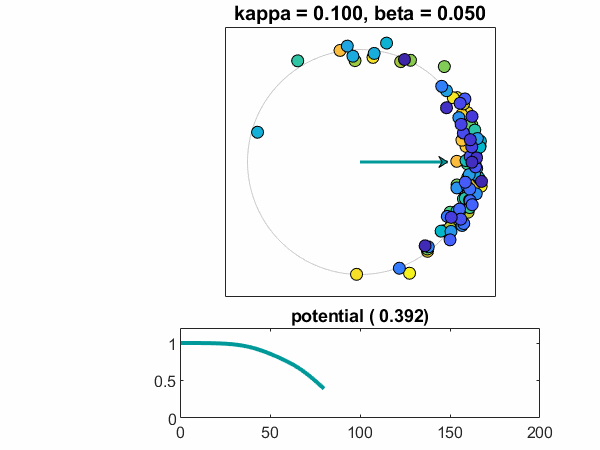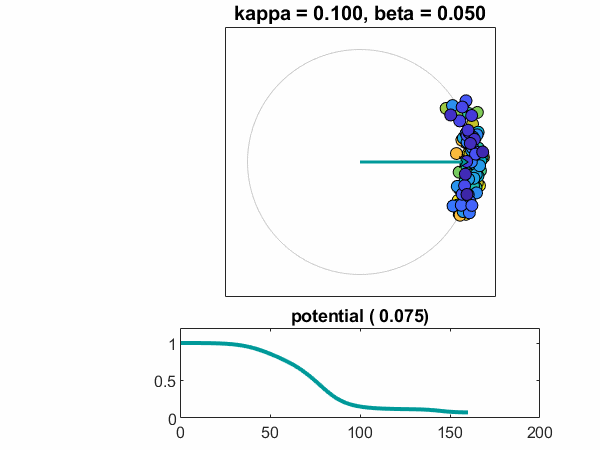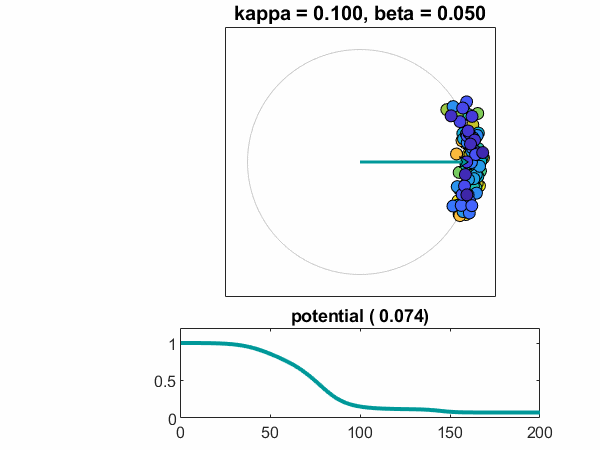
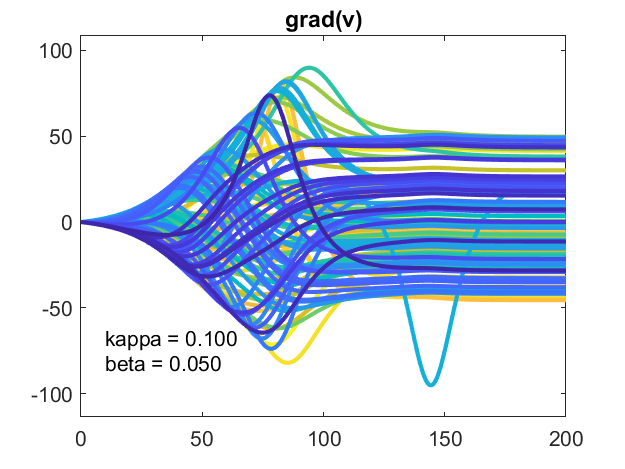
n = 100，kappa = .10，beta = .05

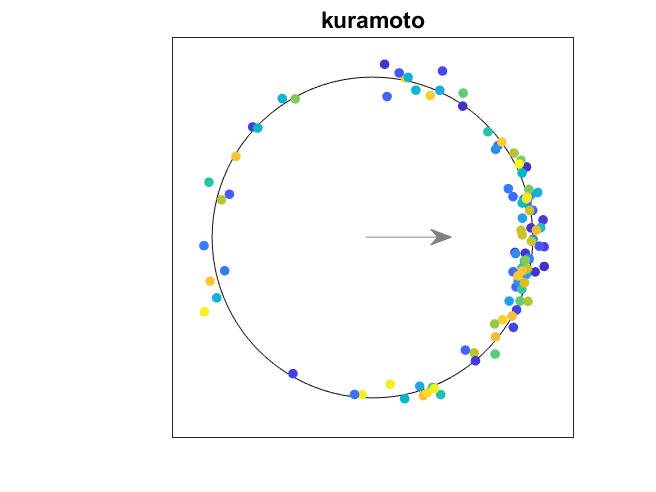
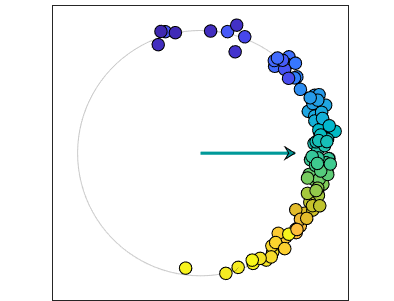
最后，让我们增加人口的大小n = 100.。而且，对于此帖子中的第一个案例引入了一些随机性。欧米茄从正态分布中采样，以围绕一个为中心，标准偏差bet。随机数发生器已设置RNG.因此，我在每次运行时都会获得相同的样本。观看单个振荡器，彩色蓝绿色，赶上其他振荡器。振荡器接近稳定，锁相配置。潜力接近常数非零值。

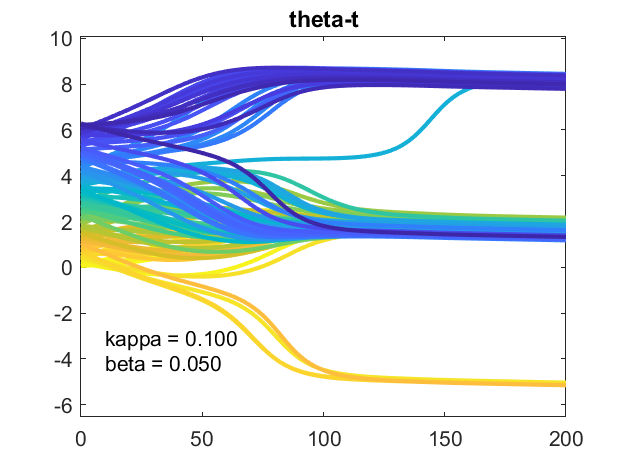
的情节Theta-T.显示振荡器的演变为三个稳定的团块，用2 \ pi $的倍数分开。许多快速振荡器，彩色的蓝色色调，形成一个丛。一些慢振荡器，彩色的黄色色调，形成慢的包装。大多数是在一个中央组织。蓝绿色的家伙比决定加入哪个丛的其他人慢。动画观看世界mod $ 2 \ pi $，因此只看到一个丛。（如果我还在使用我们的喷射彩色地图，快速和慢群将是红色和蓝色的，唤起政治比喻。我不会去那里。）

这张照片在随机抽样中强烈取决于。再次运行模拟可以产生不同数量的团块。