兰伯特W函数值得我们更好地了解。它出现在各种各样的地方。我们用MATLAB函数来求函数值是哈雷法的一个很好的应用。

内容

约翰·兰伯特

约翰·亨里奇·兰伯特于1728年出生在当时位于瑞士的米卢斯，但现在在法国。他是著名的瑞士数学家莱昂纳德·欧拉的同代人。他的兴趣非常广泛。他是第一个证明$\pi$是非理性的人。他引入了双曲三角函数。他对光学做出了如此重要的贡献，以至于光度单位是以他的名字命名的。他还在物理学、天文学、逻辑学和哲学方面做出了贡献。

兰伯特没有明确地描述这个现在以他的名字命名的函数。他考虑了各种方程，包括$x = q + x^m$这种形式的方程。欧拉随后发表了关于兰伯特工作的论文。分析这类方程所涉及的思想构成了我们今天所说的兰伯特W函数的基础。

枫木的连接

在20世纪90年代早期，Maple符号代数软件的开发人员，包括Rob Corless, Gaston Gonnet, d.e. Hare和David Jeffrey，开始意识到这个函数在这些年里已经被重新发现了很多次。他们把这个函数命名为“W”，在Maple技术通讯上发表了一篇注释，并开始开发参考书目。Don Knuth通过贡献涉及树木枚举的应用程序加入了该组织。1996年，他们五人写了一篇32页的论文，成为朗伯特W函数的权威参考文献。他们的参考书目有72条。

初等函数

让我们画一个初等函数，用$w$作为自变量。函数是$w \mbox{e}^w$。

F = @(w) w.*exp(w);Ezplot (f，[-4 1]) xlabel(' w ')轴([-4 1 -。5 1])轴广场

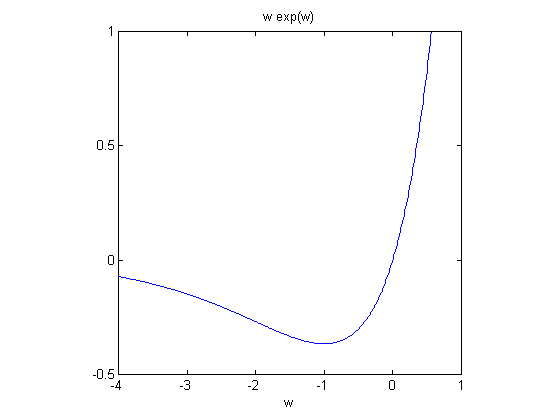
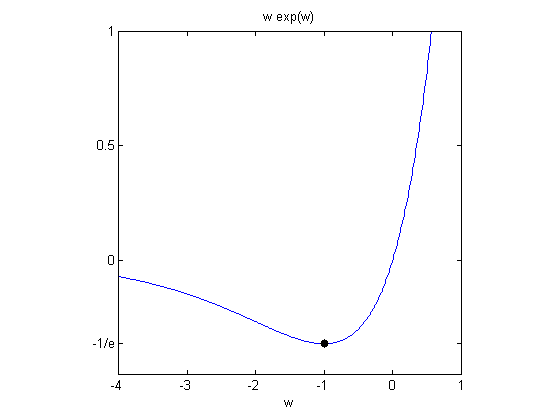
您可以看到，函数在$w = -1$处达到全局最小值。这个最小值在这里很重要，所以我们给它起个名字。

$$ \bar{\mbox{e}} = -1/\mbox{e} $$

Ebar = -1/exp(1) line([-1，-1]，[Ebar, Ebar]，“标记”，“。”，“markersize”, 18岁,“颜色”，“黑”甘氨胆酸)组(,“ytick”, ebar 0、0.5、1)集(gca,“yticklabel”, {“1 / e”，' 0 '，“0.5”，' 1 '})

Ebar = -0.367879441171442

功能逆

朗伯特W函数$W(x)$是$W \mbox{e}^ W $的函数逆。换句话说，$w$ = w ($x$)是方程的解

$$ x = w \mbox{e}^w $$

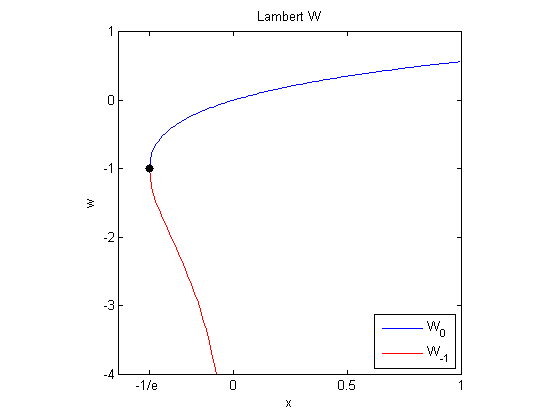
$W(x)$的图在概念上是通过将上面图的纵轴标记为“x”然后互换水平轴和垂直轴。(你可以在下面的实际图中看到一个峰值，在我们看到如何计算函数后生成。)

点$x = \bar{\mbox{e}} = -1/\mbox{e}$是至关重要的。在区间$\bar{\mbox{e}} <= x <= 0$上有两个实数解，因此$W(x)$是双值。万博 尤文图斯一个解是递增的，是定义为所有$x >= \bar{\mbox{e}}$，是已知的主要分支，用$W_0(x)$表示。另一个解是递减的，只对负$x$有定义，在0处有一个极点，用$W_{-1}(x)$表示。(还有其他复值分支$W_k(x)$，我们在这里不考虑。)

哈雷的方法

哈雷法是一种求具有连续二阶导数且易于计算的实值函数零点的方法。它是以一位以发现彗星而闻名的英国天文学家命名的。

牛顿方法用一个具有相同斜率的线性函数局部逼近一个函数，并逐步逼近该近似的零点。哈雷的方法是用斜率和曲率相同的双曲线局部逼近函数，并逐步逼近该近似的最近零点。迭代是

$ $ w_ {n + 1} = w_n-f左(w_n) / \ [f ' (w_n) - \压裂{(w_n) f”(w_n)} {2 f ' (w_n)} \] $ $

你可以通过忽略方括号中的第二项来了解牛顿的方法。你可以看到，如果比率$f' (w)/f'(w)$恰好是一个简单的形式，那么Halley的方法是特别有效的。但我们不认为Halley方法是一种通用方法，因为它需要二阶导数的知识。

申请兰伯特W

对于给定值$x$计算$W(x)$需要求解这个方程

$$ f(w) = w \mbox{e}^w - x = 0 $$

w美元。我们可以使用哈雷方法，因为所需的导数是现成的。

$ $ f ' (w) = w \ mbox {e} ^ w + w = \ \ mbox {e} ^ mbox {e} ^ w (w + 1) $ $

$ $ f”(w) = w \ mbox {e} ^ w + w \ mbox {e} ^ w + w = \ \ mbox {e} ^ mbox {e} ^ w (w + 2) $ $

请注意,

$$ f''(w)/f'(w) = (w+2)/(w+1) $$

这为我们提供了以下迭代步骤来计算给定值$x$时的兰伯特W。

$$ f_n = w_n \mbox{e}^{w_n} - x $$

$ $ w_ {n + 1} = w_n-f_n /左\ [\ mbox {e} ^ {w_n} (w_n + 1) - (w_n + 2) fn / (2 w_n + 2) \] $ $

起始值

很多人在我之前写过程序用哈雷法计算兰伯特W。他们相当重视减少最终迭代次数的起始值。我决定另辟蹊径。我愿意有计算采取更多的迭代，如果程序可以简化。实际上，我用了最简单的初始值。

对于主分支，对于任意$x$，从$w = 1$开始。完全不要尝试近似$W(x)$。对于任何$x$，迭代结果在大约六次迭代中收敛到双精度浮点精度，除了非常靠近分支点$\bar{\mbox{e}}$的值。更精确的起始值可以将迭代次数减少一半，但我更喜欢更简单的代码。

对于较低的分支，从任何小于$-1$的值开始。我选择了$w = -2$，但我认为这无关紧要。同样，大约需要六次迭代，除非$x$非常接近分支点$\bar{\mbox{e}}$或极点$0$。

停止值

哈雷法在单根附近是立方收敛的，也就是这个。一旦我们靠近了，就会很快靠近。如果连续两次迭代一致1.0 e-8，那么你就可以很确定第二个是准确的1.0 e-16．我甚至可以替换1. e-8通过Eps ^(1/3) = 6e-6．

Lambert_W.m

这是for的整个m文件函数Lambert_W．这将在适当的时候从MATLAB中央文件交换中提供。(2013年9月16日新增:见这个链接）

类型Lambert_W

function w = Lambert_W(x,branch) % Lambert_W x的函数逆= w*exp(w)。% w = Lambert_W(x)，与Lambert_W(x,0) % w = Lambert_W(x,0)主分支或上分支，W_0(x) % w = Lambert_W(x，-1)下分支，W_{-1}(x) % %参见:https://blogs.mathworks.com/cleve/2013/09/02/the-lambert-w-function/ %版权2013 The MathWorks, Inc. %有效的起始猜测如果nargin < 2 ||分支~= -1 w = ones(size(x));%从-1开始，否则w = -2*ones(size(x));%从-1开始结束v = inf*w;% Haley方法while any(abs(w - v)./abs(w) > 1.e-8) v = w;E = exp(w);F = w.*e - x;%迭代使这个量0 w = w - f / ((e。* (w + 1)——(w + 2)。* f / w + (2 * 2)));结束

兰伯特W地块

我们现在可以使用这段代码来生成兰伯特W函数的两个分支的图。

%主分支X = ebar:.01:1;情节(x, Lambert_W (x, 0))%下支持有在X = ebar:.01:0;情节(x, Lambert_W (x, 1),“r”)举行从%注释轴([-。51-4 1]) axis广场Line ([ebar ebar]，[-1 -1]，“标记”，“。”，“markersize”, 18岁,“颜色”，“黑”甘氨胆酸)组(,“xtick”，[ebar 0 .5 1]) set(gca，“xticklabel”, {“1 / e”，' 0 '，“0.5”，' 1 '})集(gca,“ytick”4:1)包含(“x”) ylabel (' w ')标题(“兰伯特W”)({传奇“W_0”，“W_{1}”}，“位置”，“东南”）

确认

感谢彼得·科斯塔重新唤起了我的兴趣，感谢罗伯·科利斯一如既往地让我了解最新情况。

兰伯特W海报

点击这个链接，可以看到由科利斯和杰弗里领导的西安大略大学的小组制作的兰伯特W函数的海报。

进一步的阅读

Corless, R.， Gonnet, G.， Hare, D.， Jeffrey, D.， Knuth, Donald(1996)。"关于兰伯特W函数"计算数学进展(柏林，纽约:Springer-Verlag) 5: 329-359。< http://link.springer.com/article/10.1007%2FBF02124750>

Corless, R.， Gonnet, G.， Hare, D.， Jeffrey, D.， Knuth, Donald(1996)。"关于兰伯特W函数"PDF预印本。https://cs.uwaterloo.ca/research/tr/1993/03/W.pdf

维基百科文章。< http://en.wikipedia.org/wiki/Lambert_W_function>

NIST数学函数数字图书馆。< http://dlmf.nist.gov/4.13>

哈雷方法:达尔奎斯特，G.，比约克，A.。科学计算中的数值方法，第一卷，第648页，SIAM，费城，2008年。

获取MATLAB代码

发布与MATLAB®R2013b

发布与MATLAB®R2013b