矩阵特征值定年服务

邮寄人克里尔那2019年5月28日

14意见（过去30天）| 0.喜欢| 1条评论

这是我在会议上谈话的摘要庆祝詹姆斯·H·威尔金森诞辰一百周年在曼彻斯特大学，5月29日。

吉姆·威尔金森（Jim Wilkinson）知道，条件恶劣的简单特征值矩阵必须接近具有多重特征值的矩阵。你如何找到最近的矩阵，其中一些特征值找到了它们的配偶？

这篇演讲的大部分内容是我对2011年论文由Rafikul Alam、Shreemaye Bora、Ralph Byers和Michael Overton撰写的《通过伪光谱成分的合并来表征和构建最近的缺陷矩阵》，年线性代数及其应用，第435卷，第494-513页。奥弗顿随附代码近德福特超过1000行的MATLAB®可从他的网页。

内容

一个3乘3的例子

在上周的博文中，“特征值灵敏度示例”，我从1980年的《用户指南》中重现了这个例子。让我们暂时忘记它是如何构造的，从

A=[-64 82 21；144-178-46；-771 962 248]

A=-648221144-178-46-771962248

计算的特征值为

总体安排长的λ=eig（A）

lambda=3.000000000003868 0.99999998212 1.999999999978

精确特征值为1、2和3。我们损失了大约四位数。这是通过特征值条件数预测的，

总体安排短的Kappa = Condeig（a）

kappa=833.1092 450.7228 383.7564

这些条件数来自右特征向量矩阵

[X，~]=eig（A）

X=0.0891 0.0735-0.1089-0.1782-0.1923 0.1634 0.9800 0.9786-0.9805

和左特征矢量矩阵

y = inv（x）

Y = -521.9612 628.5984 162.7621 265.12.7621 265.1820 -353.5760 -888.3940 -257.0058 275.3634 73.4302

一排y是左特征向量。它们被归一化，所以它们和右特征向量的点积是一。

Y*X

ANS = 1.0000 -0.0000 -0.0000 -0.0000 1.0000 -0.0000 -0.0000 0.0000 1.0000

在2017b中引入了一个函数，用于计算矩阵列的2-范数。

kappa=（向量范数（Y'）.*向量范数（X））'

kappa=833.1092 450.7228 383.7564

EigTool是一个开放的MATLAB软件，用于分析矩阵的特征值、伪谱和相关谱特性。它由Thomas Wright在Nick Trefethen的指导下于1999-2002年在牛津开发。现在由Mark Embree维护。

这是我们示例矩阵的伪谱。

eigtool（A）

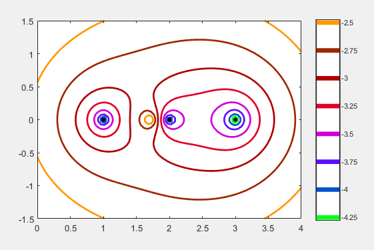
你可以看到1，2和3的三个特征值。当矩阵受到一定量的扰动时，轮廓线勾勒出特征值可以移动的区域。

此动画gif调整2和3处特征值周围的区域，直到区域合并到2.4附近的鞍点。

为了更准确地看到它们在哪里结合，我们使用函数近德福特，最近的叛逃矩阵，由纽约州教授Michael Outton撰写。输出来自近德福特是B.，最近的缺陷矩阵，以及Z.，由此产生的双重特征值。默认情况下近德福特打印有关计算的一些有用细节。

总体安排长的[B，z]=neardefmat（A）

近Defmat：距离下限为0.000299834，上限为0.00618718近Defmat：已完成，找到最低的鞍座为2.41449 + 0 i，带Dist = 0.000375171，Mu = 0，| U'* V |= 3.67335E-06奇异矢量残余规范是1.8334E-13，5.17298E-14在搜索＃3中找到了距离最近缺陷矩阵B的距离为0.000375171近Defmat：B最近的B的B型相差0.00269716和条件这些特征值的数字是272230，272669 B = 1.0E + 02 * -0.639999774916363 0.819999582124016 0.210002343527353 1.439999736641696 -1.779999511065701 -0.460002742035793 -7.710000068576393 9.620000127314574 2.479999285995845 Z = 2.414492300748820

B.是由Z.，一个svd和一个排名的一个扰动一种。

I=眼睛（3）；[U，S，V]=svd（A-z*I）；总体安排短的sigma=S（3,3）u=u（：，3）v=v（：，3）格式长的b = a  -  sigma * u * v'

西格玛=3.7517e-04 u=-0.6373 0.7457 0.1942 v=0.0941-0.1748 0.9801 B=1.0e+02*-0.639999774916363 0.8199582124016 0.210002343527353 1.43999736641696-1.7799511065701-0.460002742035793-7.7100000657639.620000031452.47992855845

这基本上就是我用来构造的扰动一种在上周的博客文章。扰动的大小是

西格玛=S（3,3）西格玛=norm（B-A）

西格玛=3.751705175569800e-04西格玛=3.751705175556183e-04

通过建设,，B.具有双重特征值，但特征值的条件是无限的，因此无法精确计算。

环境影响评估（B）

ans=2.417189453582737 2.414492295643361 1.168318252152021

弗兰克（9）

威尔金森对弗兰克矩阵家族很感兴趣。当然，我们可以在陈列室。

帮助私人/弗兰克

坦率弗兰克矩阵。f =画廊（'Frank'，N，K）是坦率的顺序矩阵N.它是具有决定因素的Upper Hessenberg 1.如果k = 1，则元素围绕抗对角线（1，n）反射 - （n，1）。F的特征值可以根据Hermite多项式的零获得。它们是阳性的并且发生在互惠成对中;因此，如果n是奇数，则1是特征值。F有地板（N / 2）不良特征值---较小的地板

9x9 Frank矩阵非常适合页面。

F=画廊('坦率'，9）

F = 9 8 7 6 5 4 3 2 11 8 8 7 6 5 4 3 2 11 0 7 7 6 5 4 3 2 11 0 0 0 6 6 5 4 3 2 11 0 0 0 0 0 00 4 4 3 2 1 0 0 0 0 0 3 3 2 1 0 0 0 0 0 0 2 2 1 0 0 0 0 0 0 0 0 1 1

矩阵显然是不对称的。因为它几乎是上三角形，你可能会认为特征值靠近对角线元素，但它们不是。在这里，分类好了。

总体安排长的[lambda，p]=排序（eig（F））；lambda

lambda=0.04480272185067 0.082015890201792 0.1625827294486328 0.3741211409126000.999999966 2.672931012564413 6.150714797051293 12.192759202150013 22.320072505788492

这里是相应的条件编号。

总体安排短的E.kappa=condeig（F）；kappa=kappa（p）

kappa=1.4762e+04 2.5134e+04 1.1907e+04 1.5996e+03 6.8615e+01 3.6210e+00 1.5268e+00 2.3903e+00 1.9916e+00

三个最小的特征值具有最大的条件数。我们期望最近的缺陷矩阵将其中两个合并在一起。

弗兰克矩阵的eigtool。

Eigtool（f）

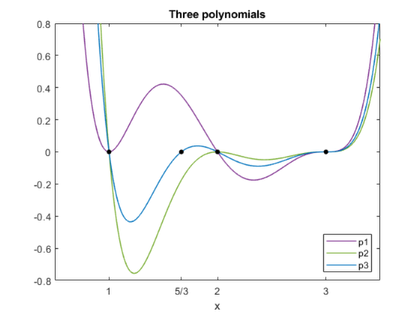
关注三个最小的特征值。红色轮廓显示包含两个合并的区域。

找到最近的有缺陷矩阵。

总体安排长的[B，z]=neardefmat（F）；

neardefmat：距离的下限为3.4791e-07，上限为8.76938e-05 neardefmat：完成后，发现的最低鞍座为0.06104+0 i，距离=5.01214e-07，μ=0，|u'*v |=6.09133e-10奇异向量残差范数为3.6435e-15，6.12511e-16该鞍点是在搜索中发现的#1到最近缺陷矩阵B的距离为5.01214e-07 neardefmat：B的两个最近计算特征值相差1.7808e-06，这些特征值的条件数为3.62946e+08，3.62937e+08

两个最小的特征值已经合并，但它们是超敏感的。

分拣（eig（B））

ans=0.061039353359070 0.061041134158948 0.168054858422710 0.373370423277969 1.000016557229929 2.672931171283966 6.150714794349185 12.1927592021295722.320722505788680

如果我们对公差不太严格，特征向量矩阵X排名缺陷，暗示矩阵B.有缺陷。

[X，~]=eig（B）；等级（X，1.e-8）

ans=8

我们可以得到一张微扰的图片ImagesC.作用首先，矩阵本身。你可以看到它的上海森堡（接近上三角形）结构。

ImagesC（F）

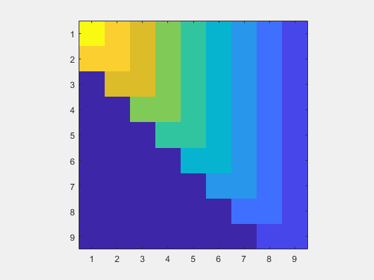
现在，扰动的图片表明它集中在右上角。

图像SC（F-B）

威尔金森（9）

对称矩阵的什么扰动使其特征值合并？威尔金森自己提供了一个很好的例子。

帮助威尔金森w = wilkinson（9）

威尔金森-威尔金森特征值检验矩阵。W=WILKINSON（n）是J.H.WILKINSON的特征值检验矩阵，Wn+。它是一个对称的三对角矩阵，其特征值对几乎相等，但并不完全相等。最常用的案例是威尔金森（21）。W=WILKINSON（n，CLASSNAME）返回类CLASSNAME的矩阵，该矩阵可以是“single”或“double”（默认值）。示例：威尔金森（7）是文档中心文档中的3 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 3参考页威尔金森W=4 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 4

W.在非对角线上是对称和三角形的。为了具有多个特征值，这种矩阵必须在子和超对角线上的某处具有一对零。但是该矩阵没有任何小的非对角线元素。然而，两个最大的特征值彼此非常接近。

λ=eig（W）

lambda=-1.125422415673319 0.254718759825861 0.95258421905215 1.822717080887109 2.178284739549981 3.1772829112892 3.24739647578982 4.745281240174140 4.747156984469142

由于矩阵是对称的，因此左和右特征向量是正交的和彼此的转子。所有特征值都是完全良好的条件。我们应该在哪里寻找聚结的特征值？

卡帕=康泰格（W）

KAPPA = 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.000000000000000 1.0000000000000001

Eigtool威尔金森（9）。9x9矩阵只有七个圆——右边的两个圆各包含两个特征值。

eigtool（西）

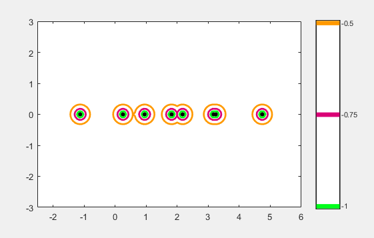
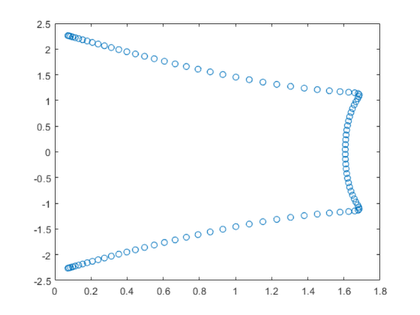
让我们放大最右边的圆圈。

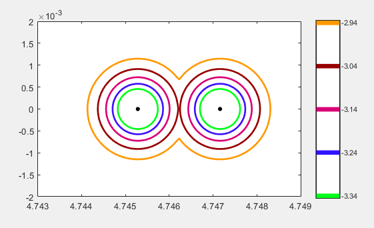
-3.04的轮廓只是勉强接吻。这是另一种鞍点，一种非光滑鞍点。你得研究一下阿拉姆等看看这为什么如此重要。

让我们看看是什么近德福特必须对威尔金森的矩阵说。

[B，z]=neardefmat（W）；

neardefmat:A在距离最近的缺陷矩阵B的公差范围内正常。B为0.000937872 neardefmat:B的两个最近的计算特征值相差2.01677e-09，这些特征值的条件数为465036、465036

果然，W.是对称的，因此是正常的。需要一种完全不同的算法。

扰动的特征值有小的虚部。

环境影响评估（B）

ans=-1.125422415673318+0.000000000i 0.254718759825861+0.000000000i 0.952584219075214+0.000000000i 1.822717080887109+0.000000000i 2.178284739549983+0.000000000i 3.177282919112890+0.000000000i 3.2473964772578982+0.000000000i 4.746219112321641+0.0010000000008i 4.746219112321641-0.000000001008386i

最后，这里是对称、三对角矩阵W和非常非对称扰动的图像W-B.这将两个特征值在一起。