罗兰关于MATLAB的艺术

将想法转化为MATLAB

锥规划与最优离散动力学

发布的罗兰美国舒尔，

638次浏览(过去30天 喜欢| 0评论
今天的客座博主是Alan Weiss，他为最优化工具箱™和其他数学工具箱编写文档。

锥编程

嗨,各位。今天的主题是圆锥规划，以及圆锥规划在火箭优化控制中的应用。自从R2020b coneprog 求解器已被用于解决圆锥规划问题。什么是圆锥规划?我认为它是二次规划的推广。所有二次规划问题都可以表示为锥规划问题。但有些锥规划问题不能用二次规划来表示。
那么，什么是圆锥规划?它是一个具有线性目标函数和线性约束的问题，类似于线性规划或二次规划。但它也包含圆锥约束。在三维[x, y, z]中，你可以将一个圆锥表示为，例如，一个圆在x-y方向上的半径小于或等于z，换句话说，圆锥约束是不等式约束
$ x^2+y^2\ z^2 $ ，
或者同样的
$ |[x,y]\|\le z $ 为非负 z ．
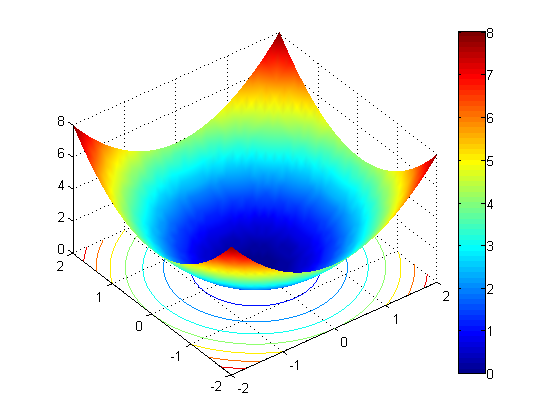
这是圆锥的边界图 $ |[x,y]\|\le z $ 为非负 z ．
(X, Y) = meshgrid (2:0.1:2);
Z =√X。^ 2 + y ^ 2);
冲浪(X, Y, Z)
视图(8,2)
包含(“x”）
ylabel (“y”）
zlabel (“z”）
当然，您可以缩放、平移和旋转圆锥约束。一般锥约束的形式定义使用一个矩阵 Asc 向量, 二元同步通信 和 d 和标量 γ 约束条件为 x 表示为
范数(Asc*x - bsc) <= d'*x - gamma;
的 coneprog 中的求解器要求您使用 secondordercone 函数表示圆锥约束。例如,
Asc =诊断接头([1,1/2,0]);
二元同步通信= 0 (3,1);
d = [0, 0, 1];
γ= 0;
socConstraints = secondordercone (Asc,二元同步通信,d,γ);
f = (1 2 0);
Aineq = [];
bineq = [];
Aeq = [];
说真的= [];
磅=(负负0);
乌兰巴托=(正,正无穷,2);
[x, fval] = coneprog (f socConstraints Aineq、bineq Aeq,说真的,磅,乌兰巴托)
找到最优解。
x = 3×1
0.4851 3.8806 2.0000
fval = -8.2462
使用基于问题的方法访问锥规划可以更简单。这个功能是在R2021a中添加的。对于前面使用基于问题的方法的示例:
x = optimvar (“x”3,“下界”(负负0),“UpperBound”,正正2);
Asc =诊断接头([1,1/2,0]);
概率= optimproblem (“客观”x - x (1) 2 * (2));
概率。约束条件= norm(Asc*x) <= x(3);
[溶胶,fval] =解决(问题)
用coneprog解决问题。找到最优解。
索尔=结构体字段:
x(3×1双):
fval = -8.2462
注意，与大多数非线性求解器不同，您不需要指定初始点 coneprog ．这在下面的示例中非常有用。

具有锥约束的离散动力学

假设你想用最少的燃料控制火箭在一个特定的地点轻轻地着陆。假设所使用的燃料与施加的加速度乘以时间成正比。不要模拟燃烧燃料时火箭重量的变化;我们假设这种控制是相对较短的时间，重量没有明显变化。负z方向有重力加速度g = 9.81。火箭上也有线性阻力作用于负速度方向，系数为1/10。这意味着时间过后 t 在没有施加任何加速度或重力的情况下，速度从 v 来 v \ exp (- t / 10)美元 ．
在连续时间中，位置的运动方程 p (t)美元 、速度 v (t)美元 ，应用加速度 美元(t)美元 是
$ {dp}{dt} = v(t) $
$ v(t) = -v(t)/10 + a(t) + g*[0,0，-1 ．
这里有一些近似的运动方程，用离散时间 N 等长步 $ t = t /N $ ：
$ p(i+i) = p(i) + t*(v(i) + v(i+1))/2 (梯形规则)
美元v (i + 1) =(我)* \ exp (- t / 10) + t *((我)+ g *[0, 0, 1])美元 (欧拉积分)。
因此,
$ p (i + 1) = p (i) + t * v (i) * (1 + \ exp (- t / 10)) / 2 + t ^ 2 *((我)+ g *[0, 0, 1]) / 2美元 ．
现在是圆锥编程的部分。假设每一步施加的加速度以一个常数为界 Amax ．这些约束
$ |a(i)\| \le {rm Amax} 对所有 我 ．
最小化的成本应该是加速度时间的规范的总和 t ．锥规划要求优化参数的目标函数是线性的。您可以通过引入新的优化变量，将此成本重新表述为线性 (我) 它们受到一组新的锥约束:
$ {rm cost} = sum s(i)*t $
$ |s(i)\| \le a(i) $ ．
假设火箭以初始速度飞行 $ v0 = [100,50，-40] $ 在位置 $ p0 = [-1000，-800,1200] $ ．计算将火箭带到指定位置所需的加速度 (0, 0, 0)美元 与速度 (0, 0, 0)美元 在时间 $ t = 40 $ ．将计算分解为100步( t = 40/100美元 ）.假设最大加速度 $ rm{Amax} = 2g $ ．
的 makeprob 函数在 脚本结束 接受的时间 T ,初始位置 p0 ，初速度 半 ，并返回一个描述离散动力学和成本的问题。
p0 =(-1000、-800、1200);
v0 = (100, -40);
概率= makeprob (p0, v0)
概率=
描述:“ObjectiveSense:‘最小化’变量:[1×1 struct] containing 4 OptimizationVariables Objective: [1×1 OptimizationExpression] Constraints: [1×1 struct] containing 4 OptimizationConstraints参见problem formulation with show。
使用比默认值小100倍的最优公差来设置选项来解决圆锥编程问题。使用 “舒尔” 线性求解器，可以更精确地求解这个问题。
选择= optimoptions (“coneprog”，“OptimalityTolerance”1 e-8“LinearSolver”，“舒尔”）;
(溶胶、成本)=解决(概率,选择=选择)
用coneprog解决问题。找到最优解。
索尔=结构体字段:
A: [99×3 double] p: [100×3 double] s: [99×1 double] v: [100×3 double]
成本= 312.7740
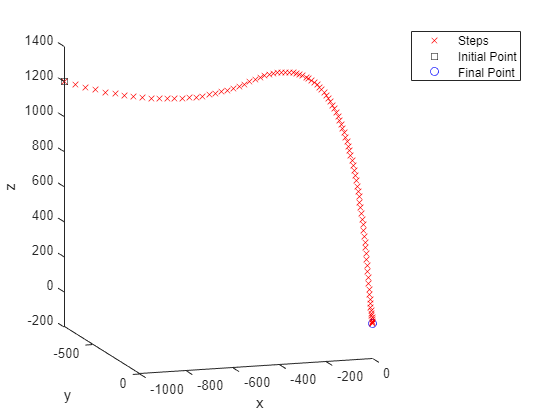
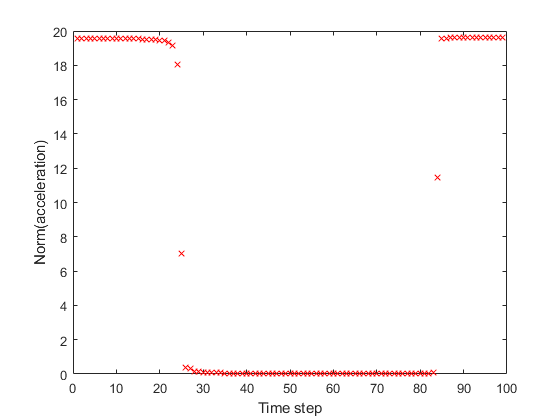
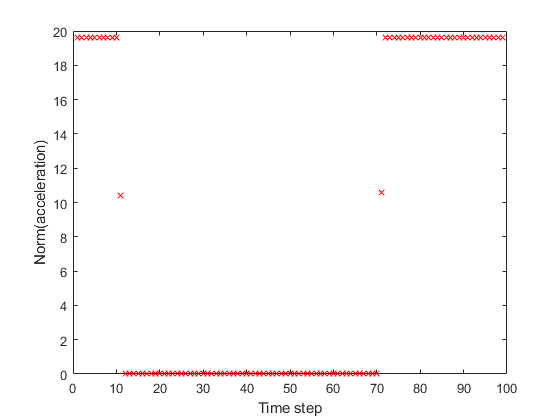
的 plottrajandaccel 函数 在这个脚本的结尾 将加速度的轨迹和范数作为时间步长的函数绘制出来。
plottrajandaccel (sol)
最佳加速度几乎是“砰砰”的。火箭加速到大约 2 g美元 起初，然后有接近零的加速度，直到近终点。接近尾声时，火箭以最大速度加速以减慢下降速度并以零速度着陆。这项控制的总成本约为313。

找到最佳的时间

找出火箭着陆的最佳时间T，这意味着火箭使用尽可能少的燃料的时间。的 findT 函数 在这个脚本的结尾 调用 fminbnd 确定成本最小的时间。我做了简单的实验，发现[20,60]是一个合理的时间范围 T 求最小值，我在 fminbnd 调用。如果你花的时间远远少于20分钟你就会遇到一个不可行的问题:
badprob = makeprob (15 p0 v0);
badsol =解决(badprob选项=选择)
用coneprog解决问题。问题是不可行的。
badsol =结构体字段:
A: [] p: [] s: [] v: []
(顺便说一句，如果你想 T 一个优化变量，那么问题就不再是 coneprog 问题。相反，这是一个问题 fmincon ，在本例中需要更长的时间来解决，并且需要您提供一个初始点。)
Topt = findT(选择)
解决……完成
Topt = 22.3294
绘制最佳轨迹和加速度。
probopt = makeprob (p0, Topt v0);
[solopt, costopt] =解决(probopt选项=选择)
用coneprog解决问题。找到最优解。
solopt =结构体字段:
A: [99×3 double] p: [100×3 double] s: [99×1 double] v: [100×3 double]
costopt = 171.1601
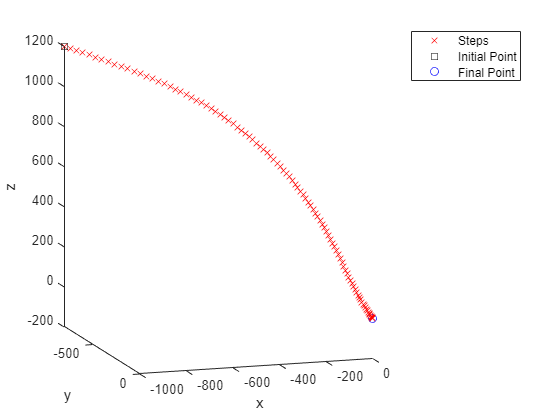
plottrajandaccel (solopt)
最优成本约为171，大约是原始参数成本的一半。这一次，控制更接近于砰的一声。火箭开始以最大速度加速，然后停止加速一段时间。同样，在最后时刻，火箭以最大速度加速，以零速度着陆。

最终的想法

圆锥规划是解决许多凸优化问题的通用框架。关于另一个重要的例子，请参见 基于问题的分段线性质量-弹簧系统的锥规划能量最小化 ．其他可以放在圆锥编程框架中的问题，请参阅Lobo、Miguel Sousa、Lieven Vandenberghe、Stephen Boyd和Hervé Lebret。“二阶锥规划的应用”。 线性代数及其应用 284年,没有。1-3(1998年11月):193-228。 https://doi.org/10.1016/s0024 - 3795 (98) 10032 - 0
你觉得锥规划或离散动力学有用吗?你有自己的例子分享吗?让我们知道 在这里 ．

辅助函数

此代码创建 makeprob 函数。
函数trajectoryproblem = makeprob (T, p0, v0)
N = 100;
g = 9.81;
pF = [0 0 0];
Amax = 2 * g;
p = optimvar (“p”N 3);
v = optimvar (“v”N 3);
一个= optimvar (“一个”n - 1 3);
s = optimvar (“s”n - 1,“下界”，0，“UpperBound”, Amax);
trajectoryproblem = optimproblem;
t = t / N;
trajectoryproblem。目标= (s)和* t;
您= optimconstr (n - 1);
为i = 1: (n - 1)
Scons (i) = norm(a(i，:)) <= s(i);
结束
acons = optimconstr (n - 1);
为i = 1: (n - 1)
acons(i) = norm(a(i，:)) <= Amax;
结束
vcons = optimconstr (N + 1, 3);
Vcons (1，:) = v(1，:) == v0;
vcons (2: N:) = v (2: N:) = = v (1: (N - 1):) * exp (- t / 10) + t * (a + repmat ([0 0 - g), N - 1, - 1));
vcons(N+1，:) = v(N，:) == [0 0 0];
pcons = optimconstr (N + 1, 3);
Pcons (1，:) = p(1，:) == p0;
pcons (2: N:) = p (2: N:) = = p (1: (N - 1):) + (1 + exp (- t / 10)) / 2 * t * v (1: (N - 1):) + t ^ 2/2 * (a + repmat ([0 0 - g), N - 1, - 1));
pcons((N+1)，:) = p(N，:) == pF;
trajectoryproblem.Constraints.acons = acons;
trajectoryproblem.Constraints.scons =您;
trajectoryproblem.Constraints.vcons = vcons;
trajectoryproblem.Constraints.pcons = pcons;
结束
此代码创建 plottrajandaccel 函数。
函数plottrajandaccel (sol)
数字
psol = sol.p;
: p0 = psol (1);
pF = psol(结束:);
plot3 (psol (: 1) psol (:, 2), psol (:, 3),“处方”）
持有在
plot3 (p0 (1), p0 (2), p0 (3),“ks”）
pF plot3 (pF (1), (2), pF (3),“波”）
持有从
视图([-10]18)
包含(“x”）
ylabel (“y”）
zlabel (“z”）
传奇(“步骤”，“起点”，“最后一点”）
数字
asolm = sol.a;
nasolm =√sum (asolm。^ 2,2));
情节(nasolm“处方”）
包含(“时间步”）
ylabel (“规范(加速度)”）
结束
此代码创建 fvalT 函数，使用的是 findT ．
函数Fval = fvalT (T,选择)
p0 =(-1000、-800、1200);
v0 = (100, -40);
tprob = makeprob (T, p0, v0);
选择= optimoptions(选择,“显示”，“关闭”）;
[~, Fval] =解决(tprob选项=选择);
结束
此代码创建 findT 函数。
函数Tmin = findT(选择)
disp (“解决……”）
Tmin = fminbnd (@ (T) fvalT (T,选择),20岁,60);
disp (“完成”）
结束
版权所有:The MathWorks, Inc.
|
类别:
新特性,
优化
  • 打印
  • 发送电子邮件

另请参阅

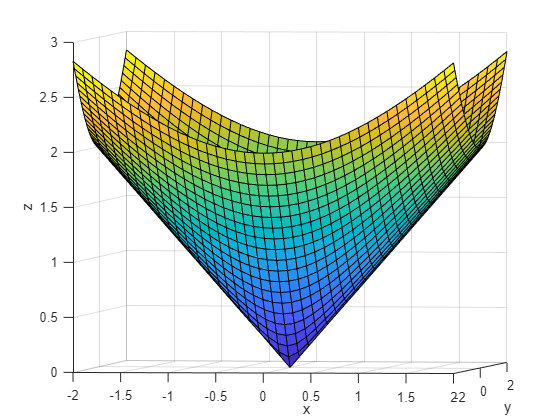
评论

要留下评论，请点击在这里登录到您的MathWorks帐户或创建一个新帐户。