确定马尔可夫链的渐近性质
这个例子展示了如何计算一个马尔可夫链的平稳分布，估计它的混合时间，并确定该链是否遍历和可约。这个例子还展示了如何在不妥协渐近行为的情况下从链中删除周期性。
考虑这个理论上的随机过程的右随机转移矩阵。
创建以转移矩阵为特征的马尔可夫链P．绘制链的有向图，并使用边缘颜色表示转移概率。
P = [0 0 1/4 1/4 0 0;0 0 1/3 0 2/3 0 0;0 0 0 0 1/3 2/3;0 0 0 0 0 1/2;0 0 0 0 3/4;1/2 0 0 0 0 0 0;1/4 3/4 0 0 0 0 0 0];mc = dtmc (P);图;graphplot (mc,“ColorEdges”,真正的);
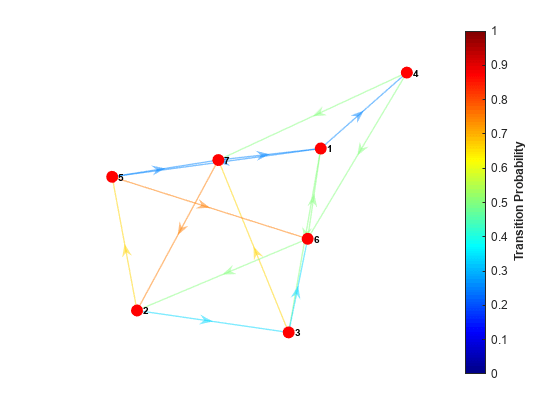
由于转移矩阵是正确随机的，马尔科夫链具有平稳分布 这样 ．
确定马尔可夫链是否不可约。
总和生育率= isreducible (mc)
总和生育率=逻辑0
总和生育率= 0表示链是不可约的。这个结果表明
是独一无二的。
确定马尔可夫链是否遍历。
tfErg = isergodic (mc)
tfErg =逻辑0
tfErg = 0表示该链不是遍历的。这个结果表明
不是任意初始分布的极限分布。
你可以用两种方法来确定一个马尔可夫链是否具有周期性。
不可约而非遍历的链是周期性的。前一节的结果表明马尔可夫链是周期性的。
检查复平面上特征值的曲线图。特征值图表明了马尔科夫链是否具有周期性，并揭示了该链的周期。
绘制复平面上的马尔可夫链的特征值。
图;eigplot (mc);
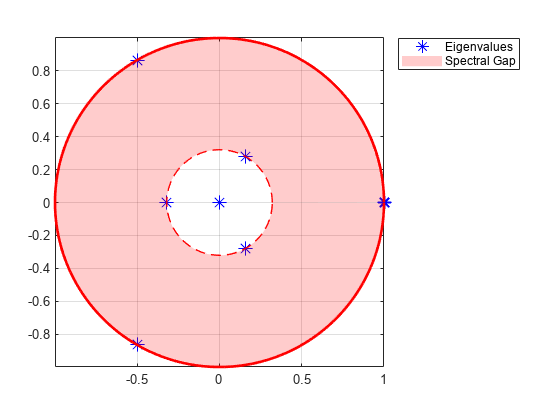
特征值图的显著特征包括:
加粗的星号是Perron-Frobenius特征值。它的大小为1，对于非负转移矩阵是保证的。
单位根处的所有特征值都表示周期性。因为单位圆上有三个特征值，所以链的周期是3。
谱间隙是单位圆的周长与以第二大特征值大小为半径的圆的周长之间的面积。谱隙的大小决定了马尔可夫链的混合率。
一般来说，光谱决定了链的结构性质。
计算马尔科夫链的平稳分布。
xFix =渐近(mc)
xFix =1×70.1300 0.2034 0.1328 0.0325 0.1681 0.1866 0.1468
xFix是链的唯一平稳分布，但不是任意初始分布的极限分布。
利用两个20步重分布，可视化马尔可夫链状态分布的两个演化。对于第一次重新分发，使用默认的统一初始分发。对于第二次再分配，指定将所有权重都放在第一个状态上的初始分配。
X1 =重新分配(mc, 20);图;distplot (mc, X1);
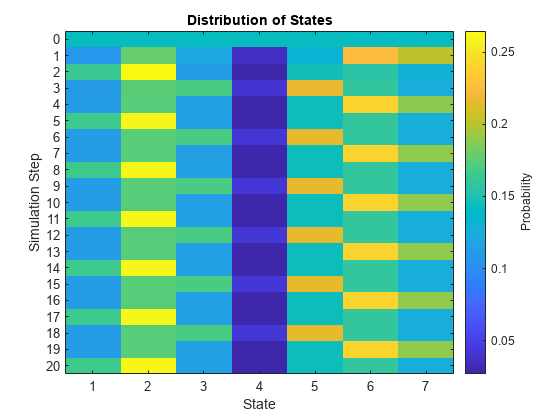
X2 =重新分配(mc 20“X0”，[1 0 0 0 0 0 0 0 0]);图;distplot (mc X2);
图中，周期性明显，状态分布不易稳定。同样，不同的初始值产生不同的演化。
通过将马尔可夫链转化为“惰性”链来消除周期性。绘制懒惰链的有向图。确定惰性链是否不可约和遍历。
lc =懒惰(mc);图;graphplot (lc);
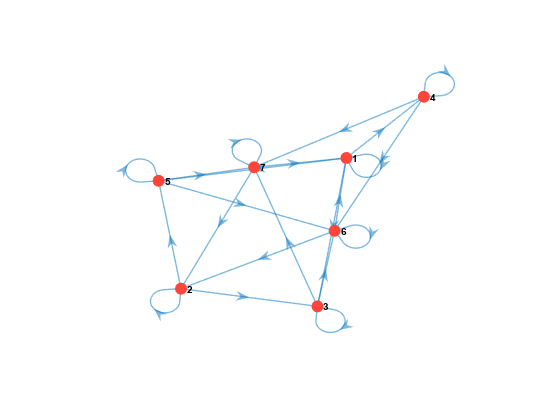
tfRedLC = isreducible (lc)
tfRedLC =逻辑0
tfErgLC = isergodic (lc)
tfErgLC =逻辑1
观察有向图中的自循环。为了消除周期性，惰性链强制状态持久性。惰性链是不可约的和遍历的。
在复平面上画出懒惰链的特征值。
图;eigplot (lc);
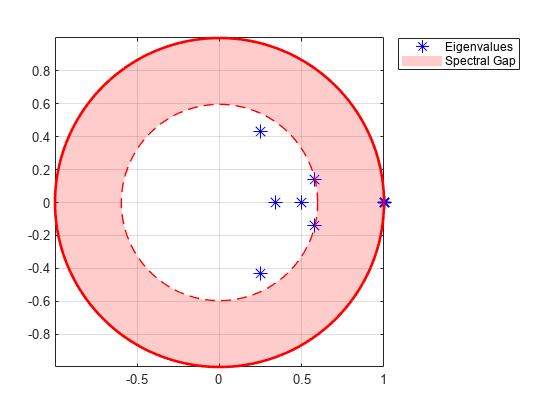
懒惰链在单位根没有任何特征值，除了Perron-Frobenius特征值。因此，惰性链的周期为1。因为惰性链的谱隙比未转化链的谱隙要小，所以惰性链比未转化链混合得更慢。
计算懒惰链的平稳分布。
xFixLC =渐近(lc)
xFixLC =1×70.1300 0.2034 0.1328 0.0325 0.1681 0.1866 0.1468
xFixLC是链的唯一平稳分布，是给定任意初始分布的极限分布。同时,xFixLC和xFix都是相同的。
通过使用10步再分配来可视化惰性链的状态分布的演变。
XLC =重新分配(lc, 10);图;XLC distplot (lc)
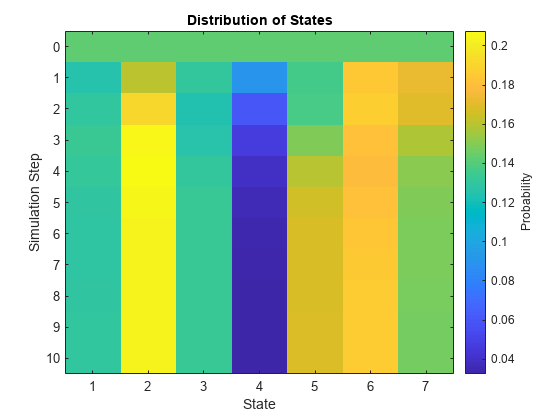
状态分布由均匀分布演化为平稳分布的时间步数小于10。注意，最后一步的颜色与中值匹配xFixLC．
另请参阅
对象
功能
相关的话题
你也可以从以下列表中选择一个网站:
