主要内容
lsqr
解线性方程组-最小二乘法
语法
描述
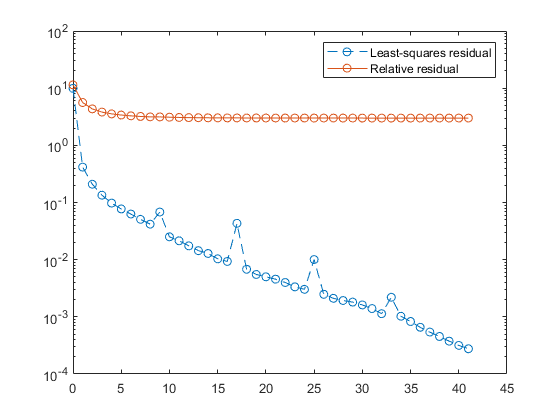
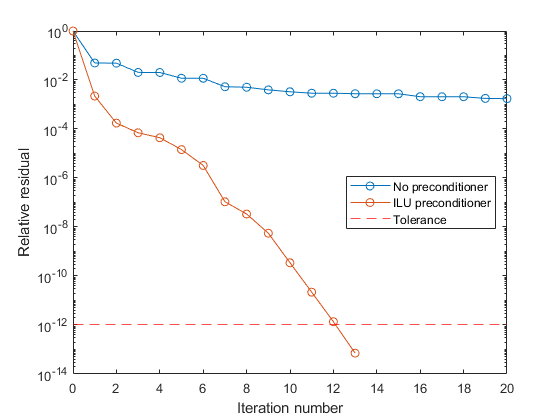
例子
输入参数
输出参数
更多关于
提示
大多数迭代方法的收敛性取决于系数矩阵的条件数,
条件(A).您可以使用平衡改进的条件数一个,这使大多数迭代解算器更容易收敛。然而,使用平衡当你随后分解均衡矩阵时,也会得到质量更好的预处理矩阵B = R * P * * C.您可以使用矩阵重新排序功能,例如
解剖和symrcm为了释放系数矩阵的行和列,并使系数矩阵被考虑为生成预处理器时最小化非安利斯数的数量。这可以减少随后解决预处理线性系统所需的存储器和时间。
工具书类
[1] Barrett, R., M. Berry, t.f. Chan, et al.,线性系统解的模板:迭代方法的构建块,暹罗,费城,1994年。
[2] Paige,C. C.和M. A. Saunders,“LSQR:稀疏线性方程和稀疏最小二乘算法,”ACM反式。数学。柔软。, 1982年第8卷,43-71页。
扩展能力
在R2006A之前介绍