QR分解通常是求解许多不同矩阵问题(包括线性系统、特征值和奇异值)的算法的第一步。住户反映是计算QR分解的首选工具。

内容

阿尔斯通户主

Alston Householder(1904-1993)是现代数值线性代数的先驱之一。从1946年到1969年，他在橡树岭国家实验室的数学部门工作了20多年，也是田纳西大学的一名教授。

阿尔斯通同时担任暹罗和ACM的主席。他介绍了他所谓的基本的埃尔米特矩阵在1958年ACM杂志的一篇论文中。

阿尔斯通是加特林堡数字代数会议组织委员会的负责人。1964年委员会的照片可以在MATLAB中找到演示目录中。

负载卡特林图像(X) colormap(地图)

加特林堡会议现在被称为户主会议。我在MATLAB新闻与笔记。

皮特•斯图尔特

我的同事和朋友G. W. Stewart是马里兰大学计算机科学系的名誉教授。大家都叫他“皮特”。他从来没有能向我满意地解释“皮特”的起源。不知何故，他的父亲、祖父甚至曾祖父都给他起了个外号叫“皮特”。

皮特是户主博士就读于田纳西大学。

皮特写了几本关于数值线性代数的书。我今天博客的参考资料是他的书“矩阵算法，卷一:基本分解”，由SIAM出版。他的伪代码已经准备好了MATLAB。

QR分解

QR分解将矩阵表示为正交矩阵和上三角矩阵的乘积。字母Q代替了“正交”中的字母O，字母R代替了“右”中的字母“上”。

分解可以从MATLAB函数中显式得到qr。但更重要的是，分解是用反斜杠表示的基本MATLAB线性方程求解器的一部分。”\，以及两者eig和圣言会稠密矩阵的函数。

对于任何矩阵，我们写

$$ A = QR $$

基于正交矩阵的运算在数值计算中是非常理想的，因为它们不会放大错误，无论是从底层数据继承的错误，还是由浮点运算引入的错误。

一个很好的例子，选自维基百科页面上的“QR分解”，是不寻常的，因为$A$， $R$，和一个重整化的$Q$都有整数项。

A = [12 -51 4;6 167 -68;-4 24 -41] [Q,R] = qr(A)

A = 12 -51 4 6 167 -68 -4 24 -41 Q = -0.8571 0.3943 0.3314 -0.4286 -0.9029 -0.0343 0.2857 - 0.17429 R = -14.0000 -21.0000 14.0000 0 -175.0000 00 -35.0000

缩放$Q$以获得整数。

cQ = 175 * Q

cQ = -150.0000 69.0000 58.0000 -75.0000 -158.0000 -6.0000 50.0000 -30.0000 165.0000

让我们检查$Q$和$R$复制$A$。

QR = Q * R

QR = 12.0000 -51.0000 4.0000 6.0000 167.0000 -68.0000 -4.0000 24.0000 -41.0000

户主反射

户主映像的特征是向量$u$，根据Pete的约定，它是标准化的

$$ ||u|| = \sqrt{2} $$

通常用矩阵来定义户主反射。但我想用另一种方式来定义它，用MATLAB的匿名函数。

H = @(u,x) x - u*(u'*x);

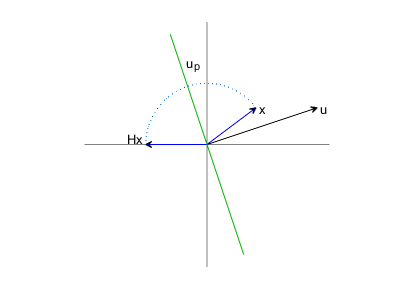
这强调了计算反射的方法。对于任意向量，求它在向量u上的投影，然后从向量x中减去它的倍数。在下面的图中，$u_p$是一条垂直于$u$的线。在更多的维度中，$u_p$是通过垂直于$u$的原点的平面。使用$u$的$\sqrt{2}$标准化，$H$的作用是将任何向量$x$转换成它在平面另一边的镜像$Hx$。(平面上的向量还剩下$H$)

house_pic

house_gen

我们从哪里得到这个向量u这就是反射的特征?我们想要对一个矩阵的列进行运算来引入对角线以下的0。我们从第一列开始，称它为x。我们想要找到u这Hx = H (u, x)是第一个元素下面的0。而且，由于反射是为了保持长度，所以它是唯一的非零元素Hx应该有abs (Hx (1)) (x) = =标准。

开始x标准化为长度为1。

u = x /规范(x)

现在添加+ 1或1来u (1)，选择匹配的符号。另一种选择是取消，在数字上不太可取。

u(1) = u(1) + (u(1))

最后,规模u通过√abs (u (1))。

u = u /√(abs (u (1)))

结果是规范(u)等于√6 (2)。再做一点代数运算，就会得到除第一个元素外的所有反射都归零的结果x。

上图说明了这种情况，因为Hx只有一个非零分量。

下面是代码，包括下面的例子x已经是0了。

类型house_gen

函数u = house_gen(x) % u = house_gen(x) %生成住户反射。% u = house_gen u (x)返回与规范(u =√(2),和% H (u (x) = x - u * (u ' * x) = - +规范(x) * e_1。修改符号函数，使符号(0)= 1。sig = @(u)符号(u) + (u==0);ν=规范(x);如果nu ~= 0 u = x/nu;u(1) = u(1) + sig(u(1));u = u /√(abs (u (1)));否则u = x;u (1) = sqrt (2); end end

让我们在矩阵的第一列试试维基百科例子

x = [12 6 -4]'

x = 12 6 -4

向量u生成的是

u = house_gen (x)

u = 1.3628 0.3145 -0.2097

产生的反射具有期望的效果。

Hx = H (u, x)

Hx = -14.0000 -0.0000 0.0000

Hx (1)等于规范(x)和其他元素Hx为零。

户主矩阵

我们的匿名函数可以用矩阵表示。这是定义户主反思的通常方式

我眼睛= (3);M = H (u,我)

M = -0.8571 -0.4286 0.2857 -0.4286 0.9011 0.0659 0.2857 0.0659 0.9560

在一般情况下

$M = I - uu'$$

与此矩阵相乘产生与匿名函数相同的反射，但需要$n^2$操作，而不是$2n$。

回想一下，高斯消去法可以用矩阵乘法的序列来描述，但它实际上是通过从其他行中减去行的倍数来实现的。这个消去操作有一个匿名函数，但它不太容易表达旋转。

house_qr

现在我们可以计算QR分解了。通过输入矩阵的列，使用户主反射在对角线下面引入0。这就得到了R矩阵。它是低效的，通常不需要实际计算qu的年代。

在这里，我们表达匿名函数的方式很重要。当x是一个矢量,u ' * x是一个标量我们可以把它写在前面u,像这样。

H = @(u,x) x - (u'*x)*u;

但我们想申请H一个矩阵同时有几列，所以我们写(u ' * x)后u,像这样,

H = @(u,x) x - u*(u'*x);

类型house_qr

函数[R,U] = house_qr(A) %户主对QR分解的反映。% [R,U] = house_qr(A)返回% R(上三角因子)和% U (house_apply使用的反射器生成器)。H = @(u,x) x - u*(u'*x);[m, n] =大小(一个);U = 0 (m, n);R =一个;对于j = 1:min(m,n) u = house_gen(R(j:m,j));U (j: m j) = U;R (j: m j: n) = H (u R (j: m j: n));R (j + 1: m j) = 0; end end

幻方的例子

以魔方为例。

=魔法(6)

A = 35 1 6 26 19 24 3 32 7 21 23 25 31 9 2 22 27 20 8 28 33 17 10 15 30 5 34 12 14 16 4 36 29 13 18 11

计算其分解。

[R U] = house_qr (A)

R = -56.3471 -16.4693 -30.0459 -39.0969 -38.0321 -38.6710 -54.2196 -34.8797 -23.1669 -25.2609 -23.2963 0 0 32.4907 -8.9182 -11.2895 -7.9245 0 0 0 0 0 0 0 -7.6283 3.9114 -7.4339 -3.4197 - -6.8393 -0.0000 U = 1.2732 0 0 0 0 0 0 0 0 0 0 0.0418 - 1.2568 0 0 0 0 0.1115 0.3884 0.4557 1.0739 0.4321 0.0451 -1.1661 0 0 0 0 0 0.4182 -0.0108 0.5942 -0.6455 1.0796 0.0558 0.5171 0.2819 -0.6558 -0.9135 1.4142

这一事实R (6,6)等于0告诉我们，6阶的幻方的秩小于6，所以是奇异的

house_apply

类型house_apply类型house_apply_transpose

函数Z = house_apply(U,X) %应用户主反射。% Z = house_apply(U,X)，使用来自house_qr %的U计算Q*X，而不实际计算Q. H = @(U,X) X - U *(U '* X);Z = X;(~ n) = (U)大小;对于j = n:-1:1 Z = H(U(:，j)，Z);端端函数Z = house_apply_转置(U,X) %应用户主转置反射。% Z = house_apply(U,X)，使用来自house_qr %的U计算Q'*X，而不实际计算Q'。H = @(u,x) x - u*(u'*x);Z = X;(~ n) = (U)大小; for j = 1:n Z = H(U(:,j),Z); end end

最后问

我们可以使用house_apply通过对单位矩阵进行变换得到QR分解的矩阵Q。

我=眼睛(大小(U));Q = house_apply (U,我)

Q = -0.6211 0.1702 - 0.4970 - 0.2062 0.5000 -0.5740 - 0.3329 - 0.3329 0.5000, 0.4560 - 0.4560 0.4562 -0.1420 -0.1420 - 0.3763 - 0.3329 -0.5324 - 0.695 0.6287 0.2096 - 0.0.220 -0.0000 -0.0710 - 0.1373 - 0.4501 - 0.3329 0.5000

检查问是正交的。

QQ =问' * Q

QQ = 1.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000—0.0000

这Q * R重新生成我们的魔方。

QR = Q * R

QR = 35.0000 1.0000 6.0000 26.0000 3.0000 32.0000 21.0000 23.0000 25.0000 9.0000 20.0000 20.0000 8.0000 28.0000 33.0000 17.0000 10.0000 30.0000 5.0000 34.0000 30.0000 16.0000 4.0000 36.0000 29.0000 18.0000 11.0000

参考

刘建民，“矩阵的三角化”，中国科学院学报，第5期，第339- 442页，1958年。< http://dl.acm.org/citation.cfm?doid=320941.320947>

g·w·斯图尔特,矩阵算法:第1卷:基本分解， SIAM, xix+458, 1998年。< http://epubs.siam.org/doi/book/10.1137/1.9781611971408>

得到MATLAB代码

发表与MATLAB®R2016a