这是一个后续我以前的帖子。经典的gramm - schmidt和改进的gramm - schmidt是向量集合正交化的两种算法。户主基本反射器可以用于相同的任务。这三种算法具有非常不同的舍入误差性质。

内容

皮特·斯图尔特

正如我在前一篇文章中所做的，我正在使用Pete Stewart的书矩阵算法，第I卷：基本分解。他的伪代码MATLAB准备。

经典gram - schmidt

经典的革兰氏施密特算法是你可能会用于生产正交向量集想到的第一件事情。对于数据集中的每个向量，删除其投影到数据集，规范还剩下什么，并将其包含在正交集。下面是代码。X是原始的向量集合，问是所得正交向量的集合，和R是一组系数，组织成一个上三角矩阵。

类型GS

函数[Q,R] = gs(X) %古典格拉姆施密特。(Q, R) = gs (X);“矩阵算法”，第1卷，1998年。(氮、磷)= (X)大小;Q = 0(氮、磷);R = 0 (p, p);对于k = 1:p Q(:，k) = X(:，k);如果k ~= 1 R(1:k-1,k) = Q(:，k-1)'*Q(:，k);Q(:，k) = Q(:，k) - Q(:，1:k-1)*R(1:k-1,k);end R(k,k) = norm(Q(:，k)); Q(:,k) = Q(:,k)/R(k,k); end end

修改gram - schmidt

这是一个相当不同的算法，不只是经典的施密特的简单修改。我们的想法是对正交新兴的向量集，而不是对原来的设置。有两种型号，面向列的一个和面向行的一个。它们产生相同的结果，在不同的顺序。这里是列版本，

类型毫克

函数[Q,R] = mgs(X) % Modified Gram-Schmidt。(Q, R) =毫克(X);“矩阵算法”，第1卷，1998年。(氮、磷)= (X)大小;Q = 0(氮、磷);R = 0 (p, p);对于k = 1:p Q(:，k) = X(:，k);对于i = 1:k-1 R(i,k) = Q(:，i)'*Q(:，k);Q(:，k) = Q(:，k) - R(i,k)*Q(:，i);end R(k,k) = norm(Q(:，k))'; Q(:,k) = Q(:,k)/R(k,k); end end

一家之主思考

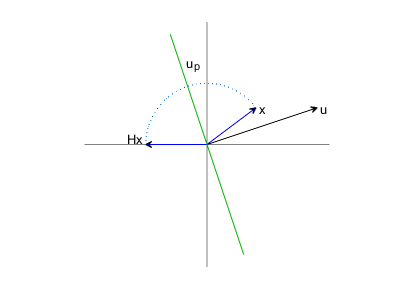
计算R通过对户主的反思X一次一列。不需要计算问，只需保存产生反射的向量。查看描述和代码我以前的文章。

类型house_qr

函数[U,R] = house_qr(A) %户主对QR分解的反映。% [U,R] = house_qr(A)返回% U，即house_apply使用的反射器生成器。% R，上三角因子。H = @(u,x) x - u*(u'*x);[m, n] =大小(一个);U = 0 (m, n);R =一个;对于j = 1:min(m,n) u = house_gen(R(j:m,j));U (j: m j) = U;R (j: m j: n) = H (u R (j: m j: n)); R(j+1:m,j) = 0; end end

比较

对于各种矩阵X，让我们来看看这三种算法在准确性和正交性这两个任务上的表现。有多亲密Q * [R来X？而且，多么接近问‘*问来我。

类型compare.m

函数比较(X);% (X)进行比较。比较三个QR分解。我=眼睛(大小(X));qrerr = 0 (1、3);ortherr = 0 (1、3);%%经典Gram Schmidt [Q,R] = gs(X);qrerr(1) =规范(Q * r×,正)/规范(X,正);ortherr(1) =规范(Q *我,正);g施密特[Q,R] = mgs(X); qrerr(2) = norm(Q*R-X,inf)/norm(X,inf); ortherr(2) = norm(Q'*Q-I,inf); %% Householder QR Decomposition [U,R] = house_qr(X); QR = house_apply(U,R); QQ = house_apply_transpose(U,house_apply(U,I)); qrerr(3) = norm(QR-X,inf)/norm(X,inf); ortherr(3) = norm(QQ-I,inf); %% Report results fprintf('\n Classic Modified Householder\n') fprintf('QR error %10.2e %10.2e %10.2e\n',qrerr) fprintf('Orthogonality %10.2e %10.2e %10.2e\n',ortherr)

好空调。

首先，尝试一个好的条件矩阵，奇数阶的幻方。

n = 7;X =魔法(n)

X = 30 39 48 1 10 19 28 38 47 7 9 18 27 29 46 6 8 17 26 35 37 5 14 16 25 34 36 45 13 15 24 33 42 44 4 21 23 32 41 43 3 12 22 31 40 49 2 1120.

检查其状态。

kappa = conde (X)

卡帕= 8.5681

做比较。

比较（X）;

经典修正房主QR误差1.73e-16 6.09e-17 5.68e-16正交性3.20e+00 1.53e-15 1.96e-15

所有这三种算法的精度做得不错，但经典的施密特失败，正交性。

不佳的制约。

接下来，尝试一个条件很差但不完全是奇异的希尔伯特矩阵。

n = 7;X = hilb（n）的

X = 1.0000 0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 0.5000 0.3333 0.2500 0.2000 0.1667 0.1429 0.1250 0.3333 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.2500 0.2000 0.1667 0.1429 0.1250 0.1111 0.1000 0.2000 0.1667 0.1429 0.1250 0.1111 0.1000 0.0909 0.1667 0.1429 0.1250 0.1111 0.1000 0.0909 0.0833 0.1429 0.1250 0.1111 0.1000 0.0909 0.08330.0769

检查其状态。

kappa = conde (X)

k = 9.8519 e + 08年

做比较。

比较(X)

经典修正户主QR误差5.35e-17 5.35e-17 8.03e-16正交性5.21e+00 1.22e-08 1.67e-15

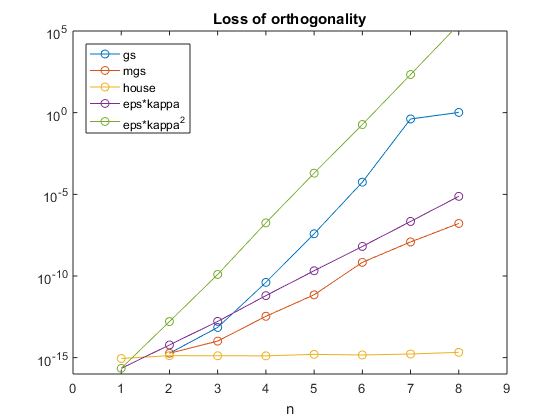
这三种算法在准确性方面都做得很好。经典的Gram-Schmidt算法在正交性方面完全失败了。矩阵的正交性取决于卡帕。户主在正交性方面做得很好。

单数。

最后，一个完全奇异的矩阵，一个偶数阶的幻方。

N = 8;X =魔法(n)

X = 64 2 3 61 60 6 7 57 9 55 54 12 13 51 50 16 17 47 46 20 21 43 42 24 40 26 27 37 36 30 31 33 32 34 35 29 28 38 39 25 41 23 22 44 45 19 18 4849 15 14 52 53 11 10 56 8 58 59 5 4 62 63 1

检查它的排名。

rankX =排名(X)

rankX = 3

做比较。

比较(X)

经典的Householder改性QR错误1.43e-16 8.54e-17 4.85e-16正交5.41e + 00 2.16e + 00 1.30E-15

同样，所有三种算法的精度做得很好。革兰氏施米茨与正交完全失败。一家之主仍与正交做得很好。

结论

这三种算法都提供了问和R在复制数据方面做得很好X， 那是

另一方面，在产生正交性时，它们的行为是非常不同的。

参考

g·w·斯图尔特,矩阵算法:第1卷:基本分解，SIAM，XIX + 458，1998。< http://epubs.siam.org/doi/book/10.1137/1.9781611971408>

得到MATLAB代码

发表与MATLAB®R2016a