基准测试分为两个步骤：

1） 在矩阵上以短精度计算LU，并计算近似解x。（在Nvidia上，半精度比DP快6倍。）

2） 以L和U为先决条件，以x为起点进行GMRES（通常需要3-4次迭代才能收敛）

基准详情如下：http://bit.ly/hpl-ai.

矩阵的任何想法？

对称希尔伯特矩阵

我研究过的第一批矩阵之一是希尔伯特矩阵。利用MATLAB中的单态展开特性，传统的对称Hilbert矩阵可以通过

总体安排老鼠n=5；i=1:nj=i'H=1./（i+j-1）

I = 1 2 3 4 5 J = 1 2 3 4 5 H = 1/2 1/2 1/4 1/5 1/5 1/2 1/2 1/3 1/4 1/5 1/6 1/3 1/41/5 1/6 1/7 1/7 1/4 1/5 1/5 1/6 1/7 1/7 1/8 1/8 1/8 1/6 1/6 1/7 1/7 1/8 1/8 1/8 1/8 1/8

当您添加行向量时我到列向量J， 所结果的i+j是一个矩阵。将此与内积,i*j，它生成标量，而外产品,j*i，产生另一种矩阵。表达方式i+j可以被认为是“外汇”。

两个标量扩展完成计算;I + J-1从和的每个元素中减去1，然后1./（i+j-1）将1除以分母中的每个元素。这两种标量扩展从最早的时候就已经在MATLAB中出现了。

希尔伯特矩阵的元素只依赖于和i+j，所以它们在antidiaconals上是恒定的。这种矩阵被称为Cauchy矩阵。求解涉及Cauchy矩阵的方程式的快速算法在$ O（n ^ 2）$时间。

非对称希尔伯特矩阵

几年前，我想要一个非对称的测试矩阵，所以我把希尔伯特矩阵分母中的加号改为减号。但这就产生了一个沿次对角线除以零的除法，所以我也将-1改为+1/2。我称之为“非对称希尔伯特矩阵”

H=1./（i-j+1/2）

H = 2/3 2/5 2/5 2/7 2/7 2/9 -2 2 2/3 2/5 2/7 -2/3 -2 2 2/3 2/5 -2/5 -2/3 -22 2/3 -2/7 -2/5 -2/3 -2 2

这些元素仅依赖于i-j这些矩阵是Toeplitz，同样，这类系统可以用$O（n^2）$运算来求解。

当我第一次计算非对称Hilbert矩阵的奇异值时，我感到惊讶——它们中的大多数几乎等于$\pi$。我们已经看到只有5乘5的小数点后五位了。

总体安排长西格玛=svd（H）

西格玛=3.141589238341321 3.14127220456508 3.12952059345258 2.921860834913688 1.461864493324889

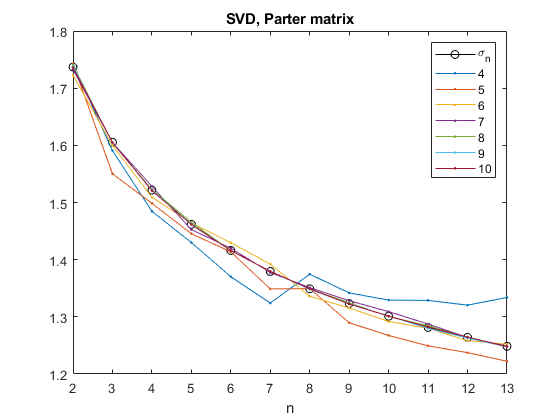
这是一个大惊喜。最终解释，提供Seymour Parter，涉及20世纪20年代的Szego定理，该定理将Toeplitz矩阵的特征值与Fourier级数和方波联系起来。

基准矩阵

我一直在杰克的同事皮托克Luszczek。这是我们对HPL-AI基准矩阵的建议。这取决于两个参数，N和亩.作为亩从1到-1，这个矩阵的核心从对称的希尔伯特矩阵到非对称的希尔伯特矩阵N在分母中，对角线上的1产生对角线优势。

A=1./（i+mu*j+n）+double（i==j）；

清楚的A.类型A.

函数aout = a（n，mu）％a（n，mu）。用于HPL-AI基准的矩阵。mu通常在[-1,1]中。我= 1：n;j = i';aout = 1./(i+mu2j+n）+眼睛（n，n）;结尾

如果亩不等于+1，这个矩阵不是cauchy。而如果亩不等于-1，它不是toeplitz。此外，如果亩大于-1，它是对角线的主导，正如我们将看到的那样，非常好的条件。

实例

这是5x5，具有合理的输出。什么时候亩是+1，我们得到对称Hilbert矩阵的一部分加上对角线上的1。

总体安排老鼠mu=1；A（n，mu）

ans=8/7 1/8 1/9 1/10 1/11 1/8 10/9 1/11 1/12 1/9 1/10 12/11 1/12 1/13 1/10 1/11 1/12 14/13 1/14 1/11 1/11 1/12 1/13 1/14 16/15

什么时候亩是-1，矩阵远非对称。远西南角的元素几乎占据了对角线。

mu = -1;a（n，mu）

ans=6/51/61/71/81/91/46/51/61/71/81/31/416/516/516/616/717/211/311/311/416/516/5

动画

这是矩阵的动画而没有添加眼睛（n，n）.作为亩走到-1到1，A（n，mu）-眼（n，n）从非对称性到对称。

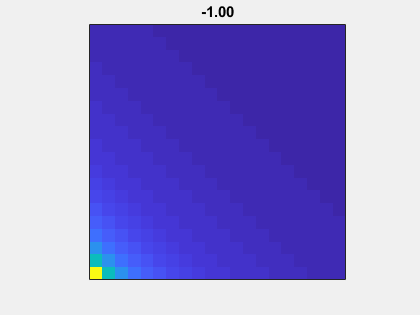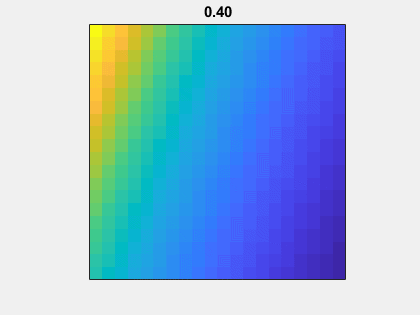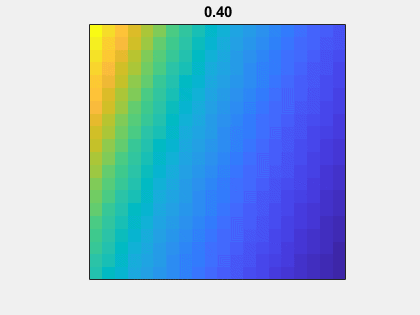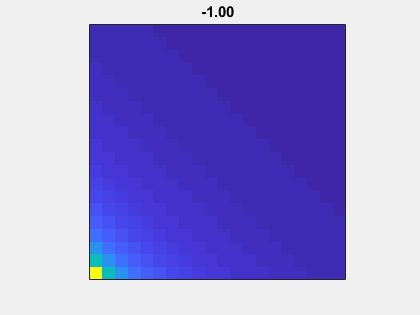
高斯消去

如果mu> -1，则最大元素位于对角线上lu（a（n，mu））没有枢转。

总体安排短的mu = -1 [l，u] = lu（a（n，mu））mu = 1 [l，u] = lu（a（n，mu））

mu=-1 L=1.0000 0 0 0.2083 0.0000 0.2778 0.1748 1.0000 0.4167 0.2265 0.1403 1.0000 0.8333 0.3099 0.1512 0.0839 1.0000 U=1.2000 0.1667 0.1429 0.1250.1111.1653 0.1369 0.1168 0.1019 0 0 1.1364 0.1115 0.0942 0 0 0 0 0 1.1058 0.0841 0 0 0 0 0 0 0 0 0 1.0545 mu=1 L=1.1090.070.070.070.0 0 0.070 0 0 0 0.0709 0.0626 1.0000 0.0795 0.0669 0.0580 0.0513 1.0000 U=1.1429 0.1250 0.1111 0.1000 0.0909 0 1.0974 0.0878 0.0800 0.0734 0 1.0731 0.0672 0.0622 0 0 1.0581 0.0542 0 0 0 1.0481

条件

让我们看看2-条件数$\sigma\u 1/\sigma\u n$如何随着参数的变化而变化。在我的笔记本电脑上计算以下图中所有矩阵的奇异值需要10分钟多一点。

西格玛1

负载hplai.mat.S1桑N亩surf（mu，n，s1）视图（25,12）xlabel('亩'）ylabel（“不”)set（gca，“xlim”,[-0.9 1.0],......'xtick',[-0.9 -0.5 0 0.5 1.0],......'ylim'，[0 2500]）标题（“\sigma_1”)

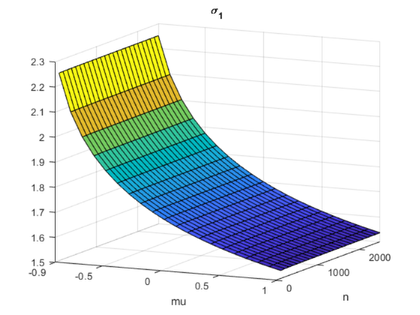
颜色随时间而变化亩从-0.9达到1.0时变化。我远离了亩= -1.0矩阵丢失对角线的优势。其他横轴是矩阵顺序N. 我有有限的N在这些实验中，我们发现了2500个。

要做的那一点是如果亩> -0.9，那么最大的奇异值是有界的西格玛1<2.3。

西格玛

冲浪（MU，N，SN）视图（25,12）Xlabel（'亩'）ylabel（“不”)set（gca，“xlim”,[-0.9 1.0],......'xtick',[-0.9 -0.5 0 0.5 1.0],......'ylim'，[0 2500]）标题（“\sigma\u n”)

如果亩>-0.9，那么最小的奇异值实际上离零有界西格玛> .75.

西格玛1/西格玛n

surf（mu，n，s1./sn）视图（25,12）xlabel('亩'）ylabel（“不”)set（gca，“xlim”,[-0.9 1.0],......'xtick',[-0.9 -0.5 0 0.5 1.0],......'ylim'，[0 2500]）标题（'\ sigma_1 / \ sigma_n')

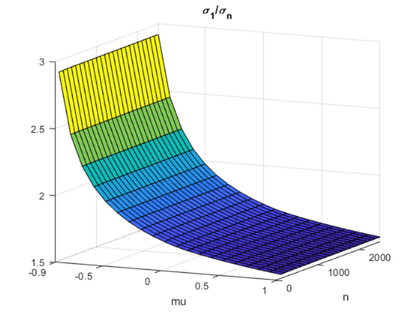
如果亩> -0.9，2-NOR中的条件号是有界的，西格玛1/西格玛n<2.3/.75$\约3.0美元。

溢流

HPL-AI基准将通过使用16位计算该矩阵的LU分解来开始半精度浮点运算，FP16。因此，如果矩阵的阶数N大于65504.这个值是最大正浮点数，可在FP16中表示的最大数字。的任何较大值N溢出到Inf.

我们必须对这件事做一些调整N> 65504.现在，我没有看到这可能是什么。

FP16的替代半精度格式是BFLOAT16，在指数中有三个比特最大正浮点数=3.39e38。使用Bfloat16生成此矩阵时，应该没有溢出问题。

谢谢

感谢Piotr Luszczek与我一起工作。我们有更多的工作要做。

获取matlab代码

与MATLAB®R2019b一起发布