多项式和矩阵的贬义流形，第2部分

저자克里夫硅藻土，2020年1月30日

18회조회(최근30일)|0좋아|0댓글

在1972年一份未发表的技术报告《保护汇流抑制不良状况》中，Velvel Kahan创造了这个描述性术语贬义的廖．以防你在日常对话中不用它，贬义的意思是“表示蔑视或不赞成。”

Velvel的报告涉及到具有多重根的多项式，这些多项式通常被轻视，因为它们的条件条件非常糟糕。但Velvel的关键观察是，尽管多根对任意扰动敏感，但它们对保持多重性的扰动不敏感。

第1部分关于多项式。这一部分是关于矩阵特征值的。

内容

管汇的

贬义流形$\mathcal{M}$现在是在$\lambda$ = 3处特征值为3的所有6 × 6矩阵的集合。当然，这些都是严格的限制，$\mathcal{M}$只是所有矩阵集合中的一个很小的子集。但如果我们停留在$\mathcal{M}$内，生活就没有那么残酷了。

两个矩阵

一个矩阵的Jordan标准形式是双对角线的，特征值在对角线上，1和0在超对角线上。在我们这里的情况下，每个有多重m的特征值都有一个m乘m的Jordan块，在超对角线上有1。不同特征值的Jordan块在超对角线上用零分隔。

我们的第一个矩阵有一个3 × 3的块，$\lambda$ = 3，然后是一个1 × 1的块，$\lambda$ = 2，最后是一个2 × 2的块，$\lambda$ = 1，所以对角线是

D = [3 3 3 2 1 1];

超对角线是

J = [1 1 0 0 1];

在这里

J1 = diag(j,1) A1 = diag(d) + J1

J1 = 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 a1 = 3 1 0 0 0 0 0 0 0 0 3 1 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 1

我们的第二个矩阵移动一个超对角线元素来交换$\lambda$ = 2和$\lambda$ = 1的倍数。

J2 = diag([1 1 0 1 0]，1) A2 = diag([3 3 3 2 2 1]) + J2

J2 = 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 a2 = 3 1 0 0 0 0 0 0 0 0 3 1 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 1

这两个矩阵被构造成两个多项式我的最后一篇文章作为特征多项式。没有必要计算这些零，它们在对角线上。

p1 = charpoly(A1，“年代”）;p2 = charpoly(A2，“年代”）;

$ $ p1 = s ^ 6-13 \ s ^ 5 + 68 \ s ^ 4 - 182 \ s ^ 3 + 261 \ s ^ 2 - 189 \ s + 54 $ $

$ $ p2 = s ^ 6日至14日\ s ^ 5 + 80 \ s ^ 4 - 238 \ s ^ 3 + 387 \ s ^ 2 - 324 \ s + 108 $ $

凸组合

凸线性组合将权值放在超对角线和对角线的新特征值上。

格式短A = 1/3* a1 + 2/3* a2

A = 3.0000 1.0000 0000 0 3.0000 1.0000 0000 3.0000 0000 000 2.0000 0.6667 0000 00 1.6667 0.3333 0000 00 1.0000

特征多项式

我们来检查一下这个特征多项式和上次的第三个多项式是一样的。

p3 = charpoly(A，“年代”）;

$ $ p3 = s ^ 6 - \压裂{41 \ s ^ 5} {3} + 76 \ s ^ 4 - \压裂{658 \ s ^ 3} {3} + 345 \ s ^ 2 - 279 \ s + 90 $ $

情节

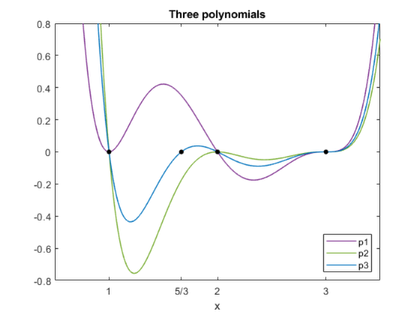
这三个多项式的图显示了三根如何比任何一个二重根更敏感，而二重根又比任何一个单根更敏感。

plot_polys (p1, p2, p3)

相似变换

相似变换保留了特征值，但掩盖了特征值。因为它很方便，我将使用我去年12月博客文章中的HPL-AI矩阵HPL-AI基准．

格式短M = hplai (6，-1)

M = 1.1667 0.1429 0.1250 0.1111 0.1000 0.0909 0.2000 1.1667 0.1429 0.1250 0.1111 0.1000 0.2500 0.2000 1.1667 0.1429 0.1250 0.1111 0.3333 0.2500 0.2000 1.1667 0.1429 0.1250 0.5000 0.3333 0.2500 0.2000 1.1667 0.1429 1.0000 0.5000 0.3333 0.2500 0.2000 1.1667

是的,女士

这是我们如何在MATLAB中做相似变换。

B = m * a / m

B = 3.0610 1.1351 0.0899 -0.1695 -0.1178 -0.2053 0.0405 3.1519 1.1018 -0.1919 -0.1296 -0.2244 0.1360 0.2922 3.2144 -0.1402 -0.0745 -0.1867 0.1096 0.3808 0.2786 1.8527 0.6013 -0.1919 0.2839 0.6709 0.4447 -0.1222 1.6349 0.1467 1.5590 1.5424 0.7469 -0.1300 -0.0449 0.7517

特征值

这对特征值有什么影响?

格式长e = eig(B)

E = 1.000000000000000 + 0.000000000000000i 1.666666666666671 + 0.000000000000000i 1.9999999999999999999900000i 3.000006294572211 + 0.000000000000000i 2.999996852713897 + 0.000005451273553i 2.999996852713897 - 0.000005451273553i

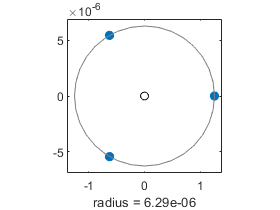
单根几乎没有动过。多重数为3的根被精度的立方根扰动。

格式短E3 = e(4:6) - 3;R3 = abs(e3)圆(e3)

R3 = 1.0e-05 * 0.6295

特征向量

特征向量呢?

[V，~] = eig(B);imagV = imag(V) realV = real(V)

imagV = 1.0e-05 * 0 0 0 0 0 0 0 0 0 0 0.705 - 0.705 0 0 0 0 0 0.0549 -0.0549 0 0 0 0 0.0678 -0.0678 -0.0904 -0.6942 0.6942 0.6942 0.6942 -0.0664 -0.0590 -0.1017 -0.1190 0.1190 0.1190 -0.0742 -0.0683 -0.1162 -0.1487 0.1487 0.1487 -0.3413 -0.9310 -0.9488 -0.1983 0.1983 0.2883 -0.1627 -0.2975 0.2975 0.2975 -0.8870 -0.2033 -0.5950 0.5950 0.5950

最后两个向量的虚分量很小，它们的实分量几乎与第四个向量相同。所以只有前四列V都是好的特征向量。我们看到B，因此一个,是有缺陷的．它没有一个完整的线性无关的特征向量集合。

特征值的条件

帮助condeig格式短ekappa = condeig(B)

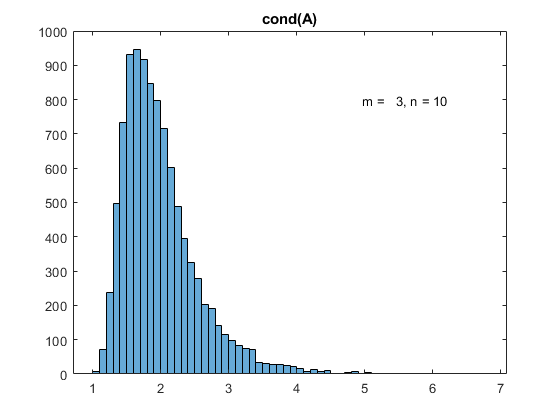
CONDEIG相对于特征值的条件数。CONDEIG(A)是A的特征值的条件数向量。这些条件数是左右特征向量夹角余弦的倒数。[V,D,s] = CONDEIG(A)等价于:[V,D] = EIG(A);s = CONDEIG(A);较大的条件数意味着A靠近具有多个特征值的矩阵。类支持输入A万博1manbetx: float: double, single参见COND。condeig文档condeig kappa = 1.6014e+00 2.9058e+00 2.9286e+00 1.3213e+10 1.3213e+10 1.3213e+10

仔细看看这些数字——前三个10的幂是0，而后三个是10。这证实了前三个特征值是条件良好的，而第四个不是。

约但标准型

一个几乎是它自己的JCF，所以这并不奇怪。

A_jcf =乔丹(A)

A_jcf = 3.0000e+00 1.0000e+00 0000 0 3.0000e+00 0000 3.0000e+00 0000 0 3.0000e+00 0000 0 1.0000e+00 0000 00 1.6667e+00 0000 000 2.0000e+00

但是关于B？通过精确的计算，它将具有相同的JCF。

格式短eB_jcf = jordan(B);real_B_jcf = real(B_jcf) imag_B_jcf = imag(B_jcf)

real_B_jcf = 1.0000e+00 0000 00 1.6667e+00 0000 000 2.0000e+00 0000 00 3.0000e+00 0000 000 3.0000e+00 0000 0000 00 3.0000e+00 imag_B_jcf = 0000 0000 0000 000 -2.7873e-06 0000 000 2.7873e-06

计算的JCF是对角线的。这又是一个事实的例子Jordan标准形式就是不能计算．也看到Golub和Wilkinson．

节奏继续…

当我试着这样做的时候，我正准备把它作为文章的结尾。我当时并没有意识到，但是使用HPL-AI矩阵进行“随机”相似性转换会产生一些可喜的结果。这个矩阵的元素是小整数的比值。

M = sym(M)

M =(7/6, 1/7, 1/8, 1/9, 1/10, 1/11)(1/5, 7/6, 1/7, 1/8, 1/9, 1/10)(1/4, 1/5, 7/6, 1/7, 1/8, 1/9][1/3、1/4、1/5,7/6,1/7,1/8][1/2、1/3、1/4、1/5、7/6,1/7][1 1/2、1/3、1/4、1/5、7/6)

的要素一个也是小整数的比值。

信谊(A)

ans = [3 1 0, 0, 0, 0] [0 3 1 0 0 0] [0 0 3 0 0 0] [0, 0, 0, 2, 2/3, 0] [0, 0, 0, 0, 5/3, 1/3] [0, 0, 0, 0, 0, 1]

的要素发票(M)是大整数的比值，但我不需要展示它们因为我们不打算求倒数米甚至是象征性的。我们用正斜杠计算相似度变换。

B = m * a / m;

的要素B也是大整数的比值。我们先看第一列;其他列也类似。

B1 = b (:，1)

B1 = 5261534240243927141/1718872313588352715 69679116377352174/1718872313588352715 46738873967260860/343774462717670543 2898457606578534/26444189439820811 97602262779214116/343774462717670543 /1718872313588352715

JCF

用这个精确的符号计算，的特征多项式B是p3．

charpoly (B,“年代”）

ans = s ^ 6 - (41 * s ^ 5) / 3 + 76 * s ^ 4 - (658 * s ^ 3) / 3 + 345 * s ^ 2 - 279 + 90

因此，JCF的B是正确的。

乔丹(B)

ans = [1, 0, 0, 0, 0, 0] [0, 5/3, 0, 0, 0, 0] [0 0 2 0 0 0] [0, 0, 0 3 1 0] [0, 0, 0, 0, 1] [0, 0, 0, 0, 0, 3]

象征性的特征向量

的符号版本的第三个输出参数eig是一个向量，它的长度是线性无关的特征向量的个数。这是几何多样性．在这个例子中，它是4。

[V,E,k] = eig(B)

V = (11/27, 463/6831, 4/9, 7/6) (25/54, 31/414, 1/2, 1/5) (15/28, 485/5796, 4/7, 1/4) (460/63, 1115/2898, 14/3, 1/3) (-23/9, -157/483, 4/5, 1/2) [1, 1, 1, 1] E = (5/3, 0, 0, 0, 0, 0] [0, 1, 0, 0, 0, 0] [0 0 2 0 0 0] [0, 0, 0 3 0 0] [0, 0, 0, 0 3 0] [0, 0, 0, 0, 0, 3] k = 1 2 3 4

检查

验证特征向量是否成立。

BV = B*V VE_k = V*E(k,k)

BV = (55/81, 463/6831, 8/9, 7/2) (125/162, 31/414, 3/5) (25/28, 485/5796, 8/7, 3/4) [2300/189, 1115/2898, 28/3, 1] [-115/27, -157/483, 8/5, 3/2] [5/3, 1, 2, 3] VE_k =(55/81, 463/6831, 8/9, 7/2)(125/162, 31/414, 3/5)(25/28, 485/5796, 8/7, 3/4)[2300/189, 1115/2898, 28/3, 1][-115/27, -157/483, 8/5, 3/2](5/3, 1、2、3)